Integraal

Integreerimine on koos oma pöördtehte diferentseerimisega üks matemaatilise analüüsi baasmõistetest.

Määratud integraal funktsioonist f(x) lõigul [a,b] on sinise ja kollase pinna pindalade vahe

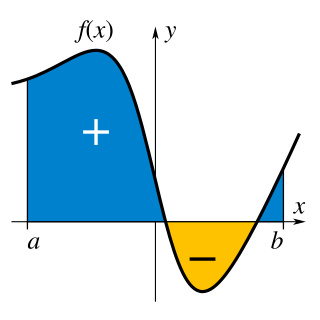
Määratud integraal reaalmuutuja funktsioonist f(x) lõigul [a,b] on suurus

${\displaystyle \int _{a}^{b}\!f(x)\,dx,\,}$

mida võib tõlgendada kui funktsiooni f(x) graafiku ja x-teljega piiratud pinna pindala. Pindala loetakse negatiivseks, kui f(x) on negatiivne, ja positiivseks, kui f(x) on positiivne.

Määramata integraal reaalmuutuja funktsioonist f(x) on funktsioon

${\displaystyle F(x)=\int \!f(x)\,dx,\,}$

kus tuletis F'(x) = f(x). Määramata integraali tundmine võimaldab arvutada määratud integraali:

${\displaystyle \int _{a}^{b}\!f(x)\,dx=F(b)-F(a).\,}$

Viimast võrdust nimetatakse Newtoni-Leibnizi valemiks.

Formaalsed definitsioonid

Integraali võib defineerida erinevalt. Järgnevalt on toodud mõned levinumad integraalide tüübid:

• Riemanni integraal defineeritakse Riemanni summa piirväärtusena; esimene range integraali käsitlus, mida ka tänapäeval kõrgema matemaatika kursustes õpetatakse;
• Darboux' integraal on samaväärne Riemanni integraaliga, kuid defineeritud Darboux' summade kaudu;
• Riemanni–Stieltjesi integraal on Riemanni integraali üldistus;
• Lebesgue'i integraal on üldisem kui Riemanni integraal. See on defineeritud mõõduteooria abil;
• Lebesgue–Stieltjes integraal, mille töötas välja Johann Radon, on Riemanni–Stieltjesi integraali ja Lebesgue'i integraali üldistus;
• Henstocki–Kurzweili integraal;
• Itō integraal ja Stratonovichi integraal on integraalid, mida rakendatakse stohhastikas;
• Haari integraal on Lebesgue'i integraal, mis kasutab Haari mõõtu.

Integraalide liigitus integreerimispiirkonna järgi

Integraale saab liigitada nende integreerimispiirkonna järgi:

• Päratu integraal
• Joonintegraal
• Pindintegraal
• Kahekordne integraal
• Kolmekordne integraal
• Kordne integraal

Vaata ka

• Numbriline integreerimine
• Liikumisintegraal
• Cauchy integraalteoreem