Hyperbeli

Hyperbeli on toisen asteen käyrä, joka määritellään seuraavasti:

Kaksi yksinkertaista hyperbeliä.

Hyperbeli on kartioleikkaus.

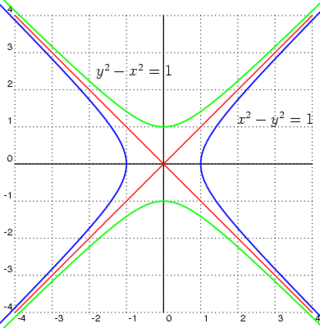
Hyperbelin muodostavat ne tason pisteet, joiden kahdesta polttopisteestä mitattujen etäisyyksien erotus on vakio. Jos valitaan polttopisteet F1 ja F2, hyperbelin pisteellä X on ominaisuus ${\displaystyle {\big |}}$ |X − F1| − |X − F2| ${\displaystyle {\big |}}$ = vakio (vertaa ellipsiin). Hyperbeli syntyy myös, kun taso leikkaa kaksiosaisen kartion molempia osakartioita.

Hyperbelin yhtälö

Origokeskinen hyperbeli

Kun suorien ${\displaystyle y={\frac {a}{b}}x}$ ja ${\displaystyle y=-{\frac {a}{b}}x}$ leikkauspiste on origossa, on hyperbelin yhtälö ${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}$, ${\displaystyle a,b\in \mathbb {R} }$ ja ${\displaystyle a>0}$. Tällöin hyperbelin huiput ovat (−a, 0) ja (a, 0).

Myös käänteislukufunktion kuvaaja on origokeskeinen hyperbeli, jonka toinen haara sijaitsee ensimmäisessä ja toinen kolmannessa neljänneksessä. Suorat, jotka ovat hyperbelien asymptootit, ovat nyt koordinaattiakselit ja ne leikkaavat origossa. Hyperbelien huiput ovat (1,1) ja (-1,-1).

Hyperbeli voidaan esittää hyperbolisten funktioiden avulla myös parametrimuodossa

${\displaystyle \left\{{\begin{matrix}x=a\cosh {t}\\y=b\sinh {t}\end{matrix}}\right.}$ , jossa ${\displaystyle a,b,t\in \mathbb {R} }$.

Yleinen hyperbeli

Hyperbeli voidaan koordinaatiston muunnoksella muuttaa muotoon, jossa hyperbelin polttopisteet ovat koordinaattiakselilla. Tämä tapahtuu muodostamalla hyperbelin kertoimista matriisi ja soveltamalla matriisiin sopivaa muunnosta.

Liittohyperbeli

Liittohyperbeli on hyperbelin erikoistapaus, joka on muotoa ${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=-1}$.

Yksikköhyperbeli

Yksikköhyperbeli on hyperbeli, jossa ${\displaystyle a=b=1}$, joten hyperbeli on muotoa ${\displaystyle x^{2}-y^{2}=1}$.

Hyperboloidi

Hyperbeliä vastaava kolmiulotteinen kappale on hyperboloidi.

Katso myös

• Ympyrä
• Ellipsi
• Paraabeli
• Kartioleikkaus
• Hyperbelirata

Kirjallisuutta

• Kivelä, Simo K.: Algebra ja geometria. Espoo: Otatieto, 1989. ISBN 951-672-103-6