Arbre de probabilité

En probabilité élémentaire, un arbre de probabilité est un schéma permettant de résumer une expérience aléatoire connaissant des probabilités conditionnelles^[1].

Ces arbres sont abondamment utilisés en théorie de la décision.

Exemples

Forage pétrolier

Un exploitant de pétrole veut effectuer un forage où l'on suppute la présence de pétrole avec une probabilité p connue.

Si on effectue un test, cette probabilité pourra être rectifiée à une valeur q encore inconnue. Le test est coûteux mais peut éviter de forer un puits sec. En revanche, la réussite du test n'implique pas avec certitude que le puits ne sera pas sec.

Doit-on effectuer le test ? Doit-on forer sans effectuer le test ?

Jeu de dés et tirage

On cherche à résumer l'expérience aléatoire suivante :

On lance un dé

• Si le numéro obtenu est un multiple de 3, on extrait au hasard une boule dans l'urne 1 qui contient 3 boules noires, 4 boules blanches et 3 boules rouges
• Si le numéro obtenu n'est pas un multiple de 3, on extrait une boule dans l'urne 2 qui contient 3 boules noires et 2 boules blanches.

La première étape est de définir un univers Ω = {(1 , N) ; (1 , B) ; (1 , R) ; (2 , N) ; (2 , B)}

• U₁ = « le lancer conduit à tirer dans l'urne 1 »
• U₂ = « le lancer conduit à tirer dans l'urne 2 »

On a donc U₁ = { (1 , N) ; (1 , B) ; (1 , R) } et p(U₁) = 1/3 puis p(U₂) = 2/3.

Pour la seconde étape, on traduit ce qui se passe quand on tire dans l'urne 1 ou l'urne 2.

• Le tirage dans l'urne 1 permet de définir des probabilités conditionnelles
  • p(N sachant U₁) = 3/10
  • p(B sachant U₁) = 4/10
  • p(R sachant U₁) = 3/10.

• De même, le tirage dans l'urne 2 permet de définir des probabilités 3/5 et 2/5.

L'expérience se résume alors dans l'arbre suivant :

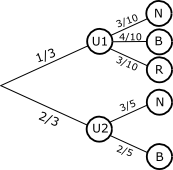
On a alors:

• Probabilité de tirer dans l'urne 1 et d'obtenir une noire :

${\displaystyle p(U_{1}\cap N)=1/3\times 3/10=1/10}$

• Probabilité de tirer dans l'urne 2 et d'obtenir une noire :

${\displaystyle p(U_{2}\cap N)=2/3\times 3/5=2/5}$

La probabilité de tirer une boule noire est alors :

${\displaystyle p(N)=p(U_{1}\cap N)+p(U_{2}\cap N)=1/2}$

Choix d'un chemin

Un homme peut aller au travail par deux chemins A ou B. La probabilité qu'il emprunte le chemin A est de 0,4. S'il emprunte le chemin A, la probabilité qu'il soit en retard est de 0,2. S'il emprunte le chemin B, la probabilité qu'il soit en retard est de 0,6. Soit R l'événement "Il est en retard" et R^c le complémentaire de R.

On en déduit les probabilités

"La probabilité qu'il emprunte le chemin A est de 0,4." : P(A) = 0,4. Comme il n'y a que deux chemins possibles alors P(B) = 1 – P(A) = 0,6.

"S'il emprunte le chemin A, la probabilité qu'il soit en retard est de 0,2." : P_A(R) = 0,2. La probabilité qu'il ne soit pas en retard sachant qu'il a pris le chemin A est donc le complémentaire P_A(R^c) = 1 – P_A(R) = 0,8.

"S'il emprunte le chemin B, la probabilité qu'il soit en retard est de 0,6." : P_B(R) = 0,6 De la même manière, P_B(R^c) = 1 – P_B(R) = 0,4.

Définitions et propriétés

On nomme arbre de probabilité un graphe orienté et pondéré obéissant aux règles suivantes

• La somme des pondérations (ou probabilités) des branches issues d'un même sommet donne 1.
• La probabilité d'un chemin est le produit des probabilités des branches qui le composent.
• La pondération de la branche allant du sommet A vers le sommet B est la probabilité conditionnelle de B sachant que A est déjà réalisé p_A(B).

On utilise alors la propriété de la probabilité conditionnelle :

${\displaystyle p(A\cap B)=p(A)\times p_{A}(B)}$ (produit des chemins).

Ainsi que la formule des probabilités totales:

si Ω₁, Ω₂,..., Ω_n définit une partition de Ω (ensembles deux à deux disjoints dont l'union donne Ω), si les Ω_i sont de probabilité non nulle, et si A est un événement de Ω,

${\displaystyle p(A)=\sum _{i=1}^{n}p(A\cap \Omega _{i})=\sum _{i=1}^{n}p(\Omega _{i})\times p_{\Omega _{i}}(A)}$

L'arbre de probabilité facilite aussi l'utilisation du théorème de Bayes :

${\displaystyle p_{B}(A)={\frac {p_{A}(B).p(A)}{p(B)}}}$

Dans l'illustration précédente, on peut répondre à la question : « Sachant que l'on a tiré une noire, quelle est la probabilité que l'on ait tiré dans l'urne 1 ? »

${\displaystyle p_{N}(U_{1})={\frac {p_{U_{1}}(N)\times p(U_{1})}{p(N)}}={\frac {1/10}{1/10+2/5}}=1/5}$