Clique (théorie des graphes)

Une clique d'un graphe non orienté est, en théorie des graphes, un sous-ensemble des sommets de ce graphe dont le sous-graphe induit est complet, c'est-à-dire que deux sommets quelconques de la clique sont toujours adjacents.

Exemple de graphe possédant une 3-clique (en rouge) : les trois sommets de ce sous-graphe sont tous adjacents deux-à-deux.

Exemple de « biclique » : le graphe biparti complet K3,3.

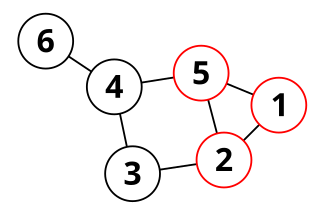
Une clique maximum d'un graphe est une clique dont le cardinal est le plus grand (c'est-à-dire qu'elle possède le plus grand nombre de sommets). Le cardinal d'une telle clique maximum est une caractéristique du graphe, appelée nombre de clique, et que l'on peut relier à son nombre chromatique. Le problème de la clique maximum, la recherche de l'une des cliques maximum pour un graphe (fini) donné, est un problème NP-difficile.

Définition

Dans la théorie des graphes, une clique est un ensemble de sommets deux-à-deux adjacents. Mais le terme « clique » est aussi souvent utilisé pour parler du graphe induit par une clique c'est-à-dire un sous-graphe induit complet^[1].

De même, on désigne couramment par le terme « biclique » un graphe biparti complet plutôt que son ensemble de sommets ou d'arêtes.

On utilise parfois le terme p-clique ou encore clique de cardinalité p pour désigner une clique contenant p sommets.

Le nombre chromatique d'un graphe est supérieur ou égal au nombre de sommets dans sa plus grande clique.

Aspects algorithmiques

Plusieurs problèmes algorithmiques sont définis à partir de cliques, notamment le problème de la clique et le problème de partition en cliques, qui font partie des 21 problèmes NP-complets de Karp^[2].