Empilement de cercles dans un carré

L'empilement de cercles dans un carré est un problème d'empilement bidimensionnel dont l'objectif est d'empiler des cercles unités identiques de nombre n dans le carré le plus petit possible. De manière équivalente, l'objectif est de disposer n points dans un carré visant à obtenir le moins de séparation, d_n, entre les points^[1].

Pour passer d'une formulations du problème à l'autre, le côté du carré des cercles unitaires sera ${\displaystyle L=2+{\frac {2}{d_{n}}}}$.

Des solutions (pas nécessairement optimales) ont été calculées pour chaque n≤10 000^[2]. Les solutions allant jusqu'à n = 20 sont indiquées ci-dessous^[2].

L'évident empilement carré est optimal pour 1, 4, 9, 16, 25 et 36 cercles (les six plus petits nombres carrés), mais il cesse d'être optimal pour les carrés plus grands à partir de 49^[2].

Nombre de cercles (n)	Longueur du côté du carré (L)	dn[1]	Densité (n/L^2)	Figure
1	2	∞	0,25
2	${\displaystyle 2+{\sqrt {2}}}$ ≈ 3,414...	${\displaystyle {\sqrt {2}}}$ ≈ 1,414...	0,172...
3	${\displaystyle 2+{\frac {\sqrt {2}}{2}}+{\frac {\sqrt {6}}{2}}}$ ≈ 3,931...	${\displaystyle {\sqrt {6}}-{\sqrt {2}}}$ ≈ 1,035...	0,194...
4	4	1	0,25
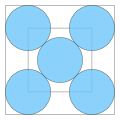
5	${\displaystyle 2+2{\sqrt {2}}}$ ≈ 4,828...	${\displaystyle {\frac {1}{2}}{\sqrt {2}}}$ ≈ 0,707...	0,215...
6	${\displaystyle 2+{\frac {12}{\sqrt {13}}}}$ ≈ 5,328...	${\displaystyle {\frac {1}{6}}{\sqrt {13}}}$ ≈ 0,601...	0,211...
7	${\displaystyle 4+{\sqrt {3}}}$ ≈ 5,732...	${\displaystyle 4-2{\sqrt {3}}}$ ≈ 0,536...	0,213...
8	${\displaystyle 2+{\sqrt {2}}+{\sqrt {6}}}$ ≈ 5,863...	${\displaystyle {\frac {1}{2}}({\sqrt {6}}-{\sqrt {2}})}$ ≈ 0,518...	0,233...
9	6	0,5	0,25
10	6,747...	0,421...  A281065	0,220...
11	7,022...	0,398...	0,223...
12	${\displaystyle 2+15{\sqrt {\frac {2}{17}}}}$ ≈ 7,144...	0,389...	0,235...
13	7,463...	0,366...	0,233...
14	${\displaystyle 6+{\sqrt {3}}}$ ≈ 7,732...	0,348...	0,226...
15	${\displaystyle 4+{\sqrt {2}}+{\sqrt {6}}}$ ≈ 7,863...	0,341...	0,243...
16	8	0,333...	0,25
17	8,532...	0,306...	0,234...
18	${\displaystyle 2+{\frac {24}{\sqrt {13}}}}$ ≈ 8,656...	0,300...	0,240...
19	8,907...	0,290...	0,240...
20	${\displaystyle {\frac {130}{17}}+{\frac {16}{17}}{\sqrt {2}}}$ ≈ 8,978...	0,287...	0,248...