Exponentielle intégrale

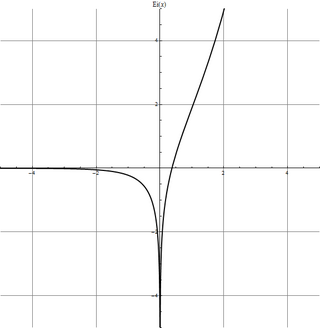
En mathématiques, la fonction exponentielle intégrale, habituellement notée Ei, est définie par :

${\displaystyle {\mbox{Ei}}:{\begin{cases}\mathbb {R} ^{*}\to \mathbb {R} \\x\mapsto {\mbox{Ei}}(x)=-\int _{-x}^{\infty }{\frac {{\rm {e}}^{-t}}{t}}\,\mathrm {d} t\,=\int _{-\infty }^{x}{\frac {{\rm {e}}^{t}}{t}}\,\mathrm {d} t.\end{cases}}}$

Comme l'intégrale de la fonction inverse (${\displaystyle t\mapsto {\frac {1}{t}}}$) diverge en 0, cette définition doit être comprise, si x > 0, comme une valeur principale de Cauchy.

Représentation graphique de la fonction exponentielle intégrale.

Lien avec le logarithme intégral

La fonction Ei est liée à la fonction li (logarithme intégral) par :

${\displaystyle {\rm {Ei}}(x)=\operatorname {li} \left(\mathrm {e} ^{x}\right).}$

Développement en série de Ei

Représentation graphique des fonctions E₁ (en haut) et Ei (en bas), pour x > 0.

L'exponentielle intégrale a pour développement en série :

${\displaystyle {\mbox{Ei}}(x)=\gamma +\ln |x|+\sum _{k=1}^{\infty }{\frac {x^{k}}{k\cdot k!}},}$

où γ est la constante d'Euler-Mascheroni.

Les fonctions En

L'exponentielle intégrale est reliée à une autre fonction, notée E₁ définie, pour x > 0, par :

${\displaystyle {\rm {E}}_{1}(x)=\int _{x}^{\infty }{\frac {{\rm {e}}^{-t}}{t}}\,\mathrm {d} t=-\int _{-\infty }^{-x}{\frac {{\rm {e}}^{t}}{t}}\,\mathrm {d} t.}$

On dispose alors de la relation, pour x > 0 :

${\displaystyle {\rm {Ei}}(-x)=-{\rm {E}}_{1}(x).}$

Les deux fonctions s'expriment en fonction de la fonction entière définie par :

${\displaystyle {\rm {Ein}}(x)=\int _{0}^{x}(1-{\rm {e}}^{-t})\,{\frac {\mathrm {d} t}{t}}=\sum _{k=1}^{\infty }{\frac {(-1)^{k+1}x^{k}}{k\;k!}}.}$

En effet, on peut montrer que, pour x > 0 :

${\displaystyle {\rm {E}}_{1}(x)=-\gamma -\ln(x)+{\rm {Ein}}(x)}$

et

${\displaystyle {\rm {Ei}}(-x)=\gamma +\ln x-{\rm {Ein}}(x).}$

La relation donnée pour E₁ permet d'étendre cette fonction sur tout ouvert simplement connexe du plan complexe ne contenant pas 0, en prenant une détermination du logarithme sur ce plan. On prend généralement comme ouvert le plan complexe privé des réels strictement négatifs.

Plus généralement, on définit, pour tout entier n strictement positif, la fonction E_n par :

${\displaystyle {\rm {E}}_{n}(x)=\int _{1}^{\infty }{\frac {{\rm {e}}^{-xt}}{t^{n}}}\,\mathrm {d} t={\frac {{\rm {e}}^{-x}}{x}}\int _{0}^{\infty }{\frac {{\rm {e}}^{-t}}{\left(1+{\frac {t}{x}}\right)^{n}}}\,\mathrm {d} t={\rm {e}}^{-x}\int _{0}^{\infty }{\frac {{\rm {e}}^{-xt}}{(1+t)^{n}}}\,\mathrm {d} t}$

Ces fonctions sont reliées par la relation :

${\displaystyle \mathrm {E} _{n}(x)={\frac {{\rm {e}}^{-x}}{x}}-{\frac {n}{x}}\mathrm {E} _{n+1}(x)}$

Calcul de E1

La fonction E₁ ne possède pas d’expression à l’aide des fonctions élémentaires usuelles, d’après un théorème dû à Liouville. Différentes méthodes peuvent être utilisées afin de calculer E₁(x) en double précision.

Pour x compris entre 0 et 2,5

On a :

${\displaystyle \mathrm {E_{1}} \left(z\right)=-\gamma -\ln z+\sum _{k=1}^{\infty }{\frac {(-1)^{k+1}z^{k}}{k\;k!}}\qquad \left(\left|\arg z\right|<\pi \right).}$

Cette série convergente peut théoriquement être utilisée pour calculer E₁(x) pour tout réel x > 0 mais avec les opérations à virgule flottante, le résultat est inexact pour x > 2,5 à cause de la perte de précision relative quand on soustrait des nombres d'ordres de grandeur différents.

Pour x > 40

Erreur relative de l'approximation asymtotique pour diverses valeurs du nombre N de termes de la somme partielle : N = 1 (rouge), 2 (vert), 3 (jaune), 4 (bleu) et 5 (rose)

Il existe une série divergente permettant d'approcher E₁ pour les grandes valeurs de Re(z), obtenue par intégration par parties^[1], qui donne le développement asymptotique suivant :

${\displaystyle \mathrm {E_{1}} (z)={\frac {\exp(-z)}{z}}\sum _{n=0}^{N-1}{\frac {n!}{(-z)^{n}}}+{\frac {N!}{(-z)^{N}}}\mathrm {E} _{N+1}(z)}$

avec ${\displaystyle \mathrm {E} _{N+1}(z)=o({\rm {e}}^{-z})}$ quand z tend vers ${\displaystyle +\infty }$.

Afin d'avoir une précision de 64 bit (double précision), il faut utiliser la valeur N = 40^[2].

Exponentielle intégrale réciproque

On peut exprimer la réciproque de l'exponentielle intégrale par le développement en série entière suivant^[3]:

${\displaystyle \forall |x|<{\frac {\mu }{\ln(\mu )}},\quad \mathrm {Ei} ^{-1}(x)=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}{\frac {P_{n}(\ln(\mu ))}{\mu ^{n}}}}$

où μ est la constante de Ramanujan-Soldner et (P_n) est la suite de polynômes définie par la relation de récurrence :

${\displaystyle P_{0}(x)=x,\ P_{n+1}(x)=x(P_{n}'(x)-nP_{n}(x)).}$

Pour ${\displaystyle n>0}$, ${\displaystyle \deg P_{n}=n}$ et on a la formule :

${\displaystyle P_{n}(x)=\left.\left({\frac {\mathrm {d} }{\mathrm {d} t}}\right)^{n-1}\left({\frac {te^{x}}{\mathrm {Ei} (t+x)-\mathrm {Ei} (x)}}\right)^{n}\right|_{t=0}.}$