Problème de couverture par ensembles

En informatique théorique, le problème de couverture par ensembles (Set Cover problem en anglais^[1]) est un problème d'algorithmique particulièrement important car c'est l'un des 21 problèmes NP-complets de Karp (Karp 1972).

Exemple d'une instance du problème de couverture par ensembles.

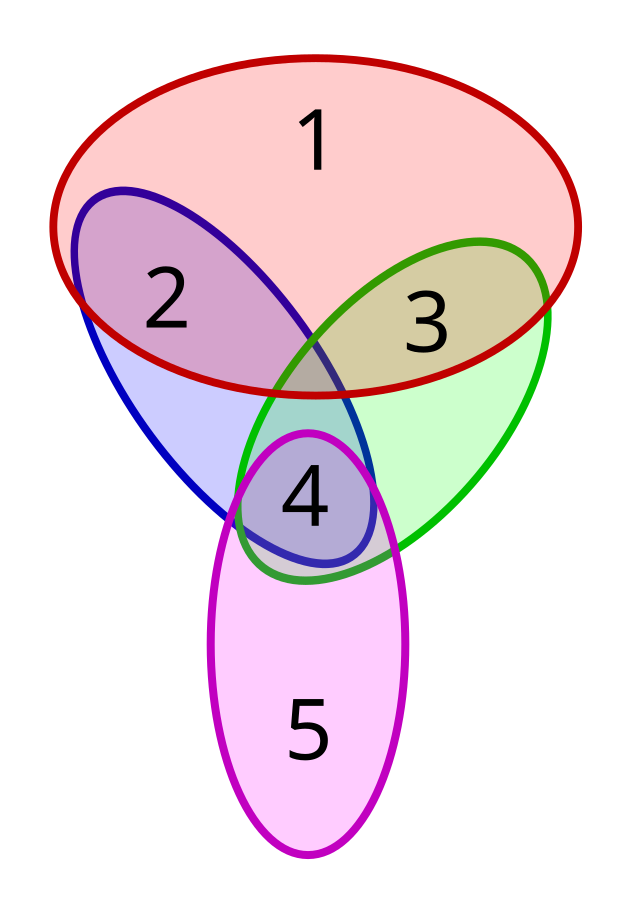
Étant donné un ensemble A, on dit qu'un élément e est couvert par A si e appartient à A. Étant donné un ensemble U et une famille S de sous-ensembles de U, le problème consiste à couvrir tous les éléments U avec une sous-famille de S la plus petite possible.

Une version plus générale consiste à assigner des poids aux éléments de S, et à chercher la sous-famille de poids minimal.

Exemple introductif

On considère un ensemble de cinq éléments à couvrir : ${\displaystyle U=\{1,2,3,4,5\}}$. On considère les sous-ensembles : ${\displaystyle \{2,4\},\{3,4\},\{4,5\}}$ et ${\displaystyle \{1,2,3\}}$. On essaye de couvrir tous les éléments avec des sous-ensembles. Par exemple ${\displaystyle \{1,2,3\},\{3,4\},\{4,5\}}$ est une couverture, puisque chaque élément est dans au moins un des sous-ensembles. La couverture qui utilise le moins de sous-ensembles est ${\displaystyle \{4,5\},\{1,2,3\}}$, c'est donc cette couverture que l'on cherche à calculer.

Définition formelle

Le problème de décision est le suivant :

Entrée : un entier ${\displaystyle k}$, un ensemble ${\displaystyle U}$ fini et ${\displaystyle S}$ un sous-ensemble de l'ensemble des parties de ${\displaystyle U}$

Question : existe-il un sous-ensemble ${\displaystyle T}$ de ${\displaystyle S}$, de taille inférieure à ${\displaystyle k}$, tel que l'union des éléments présents dans les sous-ensembles de ${\displaystyle T}$ est égale à ${\displaystyle U}$ ?

Le problème d'optimisation associé consiste à minimiser le nombre de sous-ensembles utilisés.

Le problème se généralise à une version pondérée : à chaque ensemble ${\displaystyle s\in S}$ on associe un poids ${\displaystyle c(s)}$, et le but est de minimiser la somme des poids de la couverture.

Propriétés algorithmiques et complexité

NP-complétude

Le problème de couverture par ensembles est NP-difficile (et NP-complet dans sa forme décisionnelle). Une des preuves classiques est une réduction du problème de couverture par sommets.

Formulation sous forme de programme linéaire

Il est fructueux d'exprimer ce problème comme un problème d'optimisation linéaire en nombres entiers.

En prenant une variable ${\displaystyle x_{S}}$ pour chaque sous-ensemble, le programme linéaire naturel est le suivant :

minimiser :	${\displaystyle \sum _{S\in {\mathcal {S}}}x_{S}}$		(Minimiser le nombre de sous-ensembles)
tel que :	${\displaystyle \sum _{S\colon e\in S}x_{S}\geqslant 1}$	${\displaystyle \forall e\in {\mathcal {U}}}$	(Tous les éléments sont couverts)
	${\displaystyle x_{S}\in \{0,1\}}$	${\displaystyle \forall S\in {\mathcal {S}}}$.	(Chaque sous-ensemble est, ou bien dans la couverture, ou bien pas)

Si l'on associe un poids ${\displaystyle c(S)}$ à chaque ensemble, le problème devient :

minimiser :	${\displaystyle \sum _{S\in {\mathcal {S}}}c(S)\cdot x_{S}}$		(Minimiser le poids total des sous-ensembles)
tel que :	${\displaystyle \sum _{S\colon e\in S}x_{S}\geqslant 1}$	${\displaystyle \forall e\in {\mathcal {U}}}$	(Tous les éléments sont couverts)
	${\displaystyle x_{S}\in \{0,1\}}$	${\displaystyle \forall S\in {\mathcal {S}}}$.	(Chaque sous-ensemble est, ou bien dans la couverture, ou bien pas)

Relations avec d'autres problèmes algorithmiques

• Le problème de couverture de sommets est un cas particulier de ce problème, sur un graphe.
• Le problème dual du problème de couverture par ensembles est le set packing.
• Le problème de la couverture exacte est le même problème mais avec une contrainte supplémentaire : les éléments de l'univers ne doivent être couverts qu'une seule fois.
• Le problème de couverture maximale est le même problème mais avec une contrainte supplémentaire : les éléments de l'univers ne doivent être couverts qu'un nombre maximal de fois.

Algorithmes

Algorithmes d'approximation

Le problème de couverture par ensemble étant NP-complet, de nombreux algorithmes d'approximation ont été inventés. On peut citer en exemple l'algorithme glouton, un algorithme de dual fitting, un algorithme par arrondi à partir du programme linéaire, et un schéma primal-dual^[2]. On peut analyser l'algorithme glouton avec la méthode des poids multiplicatifs^[3]. Le gap d'intégralité du LP est logarithmique.

Il existe des résultats sur la difficulté d'approximation du problème, dus d'abord à Lund et Yannakakis^[4] puis Feige^[5], puis Raz, Safra, Alon et Moshkovitz. Ce dernier résultat donne une borne inférieure de ${\displaystyle c\cdot \ln {n}}$, où ${\displaystyle c}$ est une constante, sous l'hypothèse P différent de NP^[6],[7]. Ces résultats sont basés sur les preuves interactives et le théorème PCP^[8].

Algorithmes heuristiques

Des techniques pour résoudre les problèmes de couverture comprennent les méthodes exactes, la programmation mathématique, et des méthodes heuristiques et métaheuristiques, les algorithmes génétiques ou mémétiques. Parmi ces méthodes, certains algorithmes métaheuristiques peuvent résoudre des cas volumineux du problème de couverture en un temps raisonnable. Leurs hybridations avec d'autres techniques donnent des résultats encore meilleurs, tant dans les applications de référence que dans le monde réel^[9],[10].

Importance du problème et historique

Ce problème d'optimisation combinatoire peut être lié à un large éventail d'applications du monde réel, par exemple la programmation des équipes^[11], la localisation d'installations^[12] , les problèmes de logistique urbaine^[13] et le placement optimal des caméras^{[14], [9]}

Vijay Vazirani dit dans son livre (Vazirani 2001), que «l'étude de ce problème a permis le développement de techniques qui ont ensuite été utilisées dans tout le domaine [des algorithmes d'approximation]»^[15].

Bibliographie

• (en) Vijay Vazirani, Approximation algorithms, Springer Verlag, 2001 (puis 2003), 380 p. (ISBN 978-3-540-65367-7)
• (en) Richard M. Karp, « Reducibility Among Combinatorial Problems », dans Raymond E. Miller et James W. Thatcher, Complexity of Computer Computations, Plenum, 1972 (ISBN 978-1-4684-2003-6, DOI 10.1007/978-1-4684-2001-2_9, lire en ligne), p. 85-103
• (en) Václav Chvátal, « A Greedy Heuristic for the Set-Covering Problem. », Mathematics of Operations Research, vol. 4, n^o 3,‎ 1979, p. 233-235
• Noga Alon, Dana Moshkovitz et Shmuel Safra, « Algorithmic construction of sets for k-restrictions », ACM Trans. Algorithms, ACM, vol. 2, n^o 2,‎ 2006, p. 153-177 (ISSN 1549-6325, DOI 10.1145/1150334.1150336).
• Uriel Feige, « A threshold of ln n for approximating set cover », Journal of the ACM, vol. 45, n^o 4,‎ 1998, p. 634-652 (ISSN 0004-5411, DOI 10.1145/285055.285059).
• Carsten Lund et Mihalis Yannakakis, « On the hardness of approximating minimization problems », Journal of the ACM, ACM, vol. 41, n^o 5,‎ 1994, p. 960-981 (ISSN 0004-5411, DOI 10.1145/185675.306789).
• Ran Raz et Shmuel Safra, « A sub-constant error-probability low-degree test, and a sub-constant error-probability PCP characterization of NP », dans STOC '97: Proceedings of the twenty-ninth annual ACM symposium on Theory of computing, ACM, 1997 (ISBN 978-0-89791-888-6), p. 475-484.
• Daniel Berend et S. Mamana, « A probabilistic algorithm for vertex cover », Theoretical Computer Science, vol. 983,‎ 1^er février 2024, article n^o 114306 (DOI 10.1016/j.tcs.2023.114306)