Medida da irracionalidade

En matemáticas, unha medida da irracionalidade dun número real ${\displaystyle x}$ é unha medida do "preto" que se pode aproximar mediante racionais.

Aproximacións racionais á raíz cadrada de 2.

Se unha función ${\displaystyle f(t,\lambda )}$, definida para ${\displaystyle t,\lambda >0}$, toma valores reais positivos e é estritamente decrecentes en ambas as variábeis, considere a seguinte desigualdade:

${\displaystyle 0<\left|x-{\frac {p}{q}}\right|<f(q,\lambda )}$

para un número real dado ${\displaystyle x\in \mathbb {R} }$ e números racionais ${\displaystyle {\frac {p}{q}}}$ con ${\displaystyle p\in \mathbb {Z} ,q\in \mathbb {Z} ^{+}}$. Definimos ${\displaystyle R}$ como o conxunto de todos os ${\displaystyle \lambda \in \mathbb {R} ^{+}}$ para o que só existen un número finito de ${\displaystyle {\frac {p}{q}}}$ de forma que se satisfaga a desigualdade. Entón ${\displaystyle \lambda (x)=\inf R}$ chámase unha medida da irracionalidade de ${\displaystyle x}$ en relación a ${\displaystyle f.}$ Se non hai tal ${\displaystyle \lambda }$ e o conxunto ${\displaystyle R}$ está baleiro, ${\displaystyle x}$ dise que ten unha medida de irracionalidade infinita ${\displaystyle \lambda (x)=\infty }$.

En consecuencia, a desigualdade

${\displaystyle 0<\left|x-{\frac {p}{q}}\right|<f(q,\lambda (x)+\varepsilon )}$

ten como moito só un número de finitamente moitas solucións ${\displaystyle {\frac {p}{q}}}$ para tódolos ${\displaystyle \varepsilon >0}$.

Expoñente da irracionalidade

O expoñente de irracionalidade ou medida de irracionalidade de Liouville-Roth vén dado pola función${\displaystyle f(q,\mu )=q^{-\mu }}$, unha definición que adapta a definición dos números de Liouville, o expoñente de irracionalidade ${\displaystyle \mu (x)}$ defínese para números reais ${\displaystyle x}$ sendo o supremo do conxunto de ${\displaystyle \mu }$ tal que se satisfán as desigualdades ${\displaystyle 0<\left|x-{\frac {p}{q}}\right|<{\frac {1}{q^{\mu }}}}$ por un número infinito de pares de enteiros primos ${\displaystyle (p,q)}$ con ${\displaystyle q>0}$.^[1][2]:246

Para calquera valor ${\displaystyle n<\mu (x)}$, o conxunto infinito de todos os racionais ${\displaystyle p/q}$ que satisfán a desigualdade anterior producen boas aproximacións de ${\displaystyle x}$. Pola contra, se ${\displaystyle n>\mu (x)}$, entón hai como moito finitamente moitos coprimos ${\displaystyle (p,q)}$ con ${\displaystyle q>0}$ que satisfán a desigualdade.

Outro xeito de expresalo sería^[3]

${\displaystyle \mu (x):=\inf {\bigg \{}\mu (x)\geq 0:{\text{só hai finitamente moitos racionais }}p/q{\text{ tal que }}\left|x-{\frac {p}{q}}\right|<{\frac {1}{q^{\mu }}}{\bigg \}}.}$

${\displaystyle \mu (x):=\sup {\bigg \{}\mu (x)\geq 0:{\text{hai infinitamente moitos racionais }}p/q{\text{ tal que }}\left|x-{\frac {p}{q}}\right|<{\frac {1}{q^{\mu }}}{\bigg \}}.}$

Algúns casos

Por exemplo, sempre que unha aproximación racional ${\displaystyle {\frac {p}{q}}\approx x}$ con ${\displaystyle p,q\in \mathbb {N} }$ dá ${\displaystyle n+1}$ cifras decimais exactas, entón

${\displaystyle {\frac {1}{10^{n}}}\geq \left|x-{\frac {p}{q}}\right|\geq {\frac {1}{q^{\mu (x)+\varepsilon }}}}$

para calquera ${\displaystyle \varepsilon >0}$, agás como máximo un número finito de pares "afortunados" ${\displaystyle (p,q)}$.

Un número ${\displaystyle x\in \mathbb {R} }$ con expoñente de irracionalidade ${\displaystyle \mu (x)\leq 2}$ chámase número diofantiano,^[4] mentres que os números con ${\displaystyle \mu (x)=\infty }$ chámanse números de Liouville.

Forma construtiva

Se temos que o ${\displaystyle \limsup _{n\to \infty }{\tfrac {1}{n}}{\ln |q_{n}|}\leq \sigma }$ e ${\displaystyle \lim _{n\to \infty }{\tfrac {1}{n}}{\ln |q_{n}x-p_{n}|}=-\tau }$ para algúns números reais positivos ${\displaystyle \sigma ,\tau }$, entón podemos estabelecer un límite superior para o expoñente de irracionalidade de ${\displaystyle x}$ con: ^[5][6]

${\displaystyle \mu (x)\leq 1+{\frac {\sigma }{\tau }}}$.

Corolarios

• Os números racionais teñen un expoñente de irracionalidade 1, mentres que (como consecuencia do teorema da aproximación de Dirichlet) todo número irracional ten un expoñente de irracionalidade polo menos 2.

• Por outra banda, unha aplicación do lema de Borel-Cantelli mostra que case todos os números, incluídos todos os números irracionais alxébricos, teñen un expoñente de irracionalidade exactamente igual a 2.^{[2] :246}

• Temos ${\displaystyle \mu (x)=\mu (rx+s)}$ para números reais ${\displaystyle x}$ e números racionais ${\displaystyle r\neq 0}$ e ${\displaystyle s}$. Se para algúns ${\displaystyle x}$ temos ${\displaystyle \mu (x)\leq \mu }$, entón dedúcese que ${\displaystyle \mu (x^{1/2})\leq 2\mu }$.^[7]:368 

• Para un número real ${\displaystyle x}$ dado pola súa expansión de fracción continua simple ${\displaystyle x=[a_{0};a_{1},a_{2},...]}$ con converxentes ${\displaystyle p_{i}/q_{i}}$ cúmprese:

${\displaystyle \mu (x)=1+\limsup _{n\to \infty }{\frac {\ln q_{n+1}}{\ln q_{n}}}=2+\limsup _{n\to \infty }{\frac {\ln a_{n+1}}{\ln q_{n}}}.}$

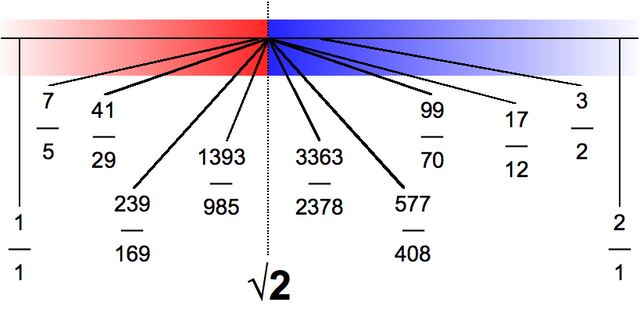
Exemplos

En primeiro lugar imos ver un non exemplo. Se temos un dos primeiros converxentes da fracción continua de pi, por exemplo ${\displaystyle {\dfrac {22}{7}}}$, daquela teríamos

${\displaystyle {\bigg |}\pi -{\dfrac {22}{7}}{\bigg |}<{\dfrac {1}{7^{\mu (\pi )}}}}$, implica ${\displaystyle \ln 0.00126=-6.676<-\mu (\pi )\ln {(7)};\quad \mu (\pi )<{\dfrac {6.676}{1.94}}=3.44}$.

Mais este converxente podería ser unha fracción "afortunada". En rigor deben procurarse secuencias con denominadores grandes e que a condición se cumpra para "finitamente moitos".

Para o exemplo da constante de Apéry (${\displaystyle \zeta (3)}$) imos seguir parte do documento de Van der Porten^[8]. Roger Apéry descobre, mediante transformacións moito elaboradas, unhas recorrencias que aceleran o cálculo de zeta de 3, sendo ${\displaystyle p(n-1)=34n^{3}-51n^{2}+27n-5}$:

${\displaystyle n^{3}a_{n}-p(n-1)a_{n-1}+(n-1)^{3}a_{n-2}=0}$,

${\displaystyle n^{3}b_{n}-p(n-1)b_{n-1}+(n-1)^{3}b_{n-2}=0}$.

E agora:

${\displaystyle a_{n}b_{n-1}-a_{n}b_{n-1}={\dfrac {6}{n^{3}}}}$,

${\displaystyle {\bigg |}\zeta (3)-{\frac {a_{n}}{b_{n}}}{\bigg |}=\sum _{k=n+1}^{\infty }{\frac {6}{k^{3}b_{n}b_{n-1}}}}$.

Isto implica

${\displaystyle \zeta (3)-{\frac {a_{n}}{b_{n}}}=O{\bigg (}{\frac {1}{b_{n}^{2}}}{\bigg )}}$.

Isto xunto da recorrencia vista enrriba para ${\displaystyle b_{n}}$ permite calculalo asintóticamente. Dado que os ceros do polinomio ${\displaystyle x^{2}-34x+1=0}$ son ${\displaystyle ({\sqrt {2}}\pm 1)^{4}}$ pódese concluír que ${\displaystyle b_{n}=O{\bigg (}\alpha ^{4n}{\bigg )}}$ con ${\displaystyle \alpha =1+{\sqrt {2}}}$.

Por último

${\displaystyle {\bigg |}\zeta (3)-{\frac {a_{n}}{b_{n}}}{\bigg |}=O(\alpha ^{8n})=O({\frac {1}{q_{n}^{1+\delta }}})}$ con ${\displaystyle \delta ={\dfrac {4\ln(\alpha )-3}{4\ln(\alpha )+3}}=0.080529\ldots }$ que dá ${\displaystyle \delta ^{-1}=12.417820\ldots }$ e así

${\displaystyle {\bigg |}\zeta (3)-{\frac {p}{q}}{\bigg |}>{\frac {1}{q^{12.417820+\epsilon }}}}$.

${\displaystyle \mu (\zeta (3))\leq 12.417820\ldots }$

(como podemos ver na táboa de embaixo este límite superior xa foi calculado cunha cantidade inferior).

Límites coñecidos

• Se ${\displaystyle \mu (x)=1,x\ }$ é racional.
• Se ${\displaystyle \mu (x)=2,x\ }$ é alxébrico de grao > 1.
• Se ${\displaystyle \mu (x)\geq 2,x\ }$ é trascendental.

Para a maioría dos números transcendentais, non se coñece o valor exacto do seu expoñente de irracionalidade.^[7] A continuación móstrase unha táboa de límites superiores e inferiores coñecidos.

Número ${\displaystyle x}$	Expoñente da irracionalidade ${\displaystyle \mu (x)}$		Notas
	Límite inferior	Límite superior
Número racional ${\displaystyle p/q}$ con ${\displaystyle p\in \mathbb {Z} ,q\in \mathbb {Z} ^{+}}$	1		Todo número racional ${\displaystyle p/q}$ ten un expoñente de irracionalidade de exactamente 1.
Número alxébrico irracional ${\displaystyle \alpha }$	2		Polo Teorema de Roth o expoñente de irracionalidade de calquera número alxébrico irracional é exactamente 2. Exemplos inclúen raíces cadradas e o número áureo ${\displaystyle \varphi }$.
${\displaystyle e^{2/k},k\in \mathbb {Z} ^{+}}$	2		Se os elementos ${\displaystyle a_{n}}$ da expansión simple da fracción continua dun número irracional ${\displaystyle x}$ están limitados por encima de ${\displaystyle a_{n}<P(n)}$ por un polinomio arbitrario ${\displaystyle P}$, entón o seu expoñente de irracionalidade é ${\displaystyle \mu (x)=2}$. Os exemplos inclúen números nos que as fraccións continuas se comportan de forma previsíbel como ${\displaystyle e=[2;1,2,1,1,4,1,1,6,1,...]}$ e${\displaystyle I_{0}(2)/I_{1}(2)=[1;2,3,4,5,6,7,8,9,10,...]}$.
${\displaystyle \tan(1/k),k\in \mathbb {Z} ^{+}}$	2
${\displaystyle \tanh(1/k),k\in \mathbb {Z} ^{+}}$	2
${\displaystyle S(b)}$ con ${\displaystyle b\geq 2}$	2		${\displaystyle S(b):=\sum _{k=0}^{\infty }b^{-2^{k}}}$con ${\displaystyle b\in \mathbb {Z} }$, ten termos de fracción continua que non superan unha constante fixa.[9][10]
${\displaystyle T(b)}$ con ${\displaystyle b\geq 2}$[11]	2		${\displaystyle T(b):=\sum _{k=0}^{\infty }t_{k}b^{-k}}$ onde ${\displaystyle t_{k}}$ é a secuencia de Thue-Morse e${\displaystyle b\in \mathbb {Z} }$. Ver Constante de Prouhet-Thue-Morse .
${\displaystyle \ln(2)}$[12][13]	2	3.57455...	Hai outros números da forma ${\displaystyle \ln(a/b)}$ para os que se coñecen os límites dos seus expoñentes de irracionalidade.[14][15][16]
${\displaystyle \ln(3)}$[12][17]	2	5.11620...
${\displaystyle 5\ln(3/2)}$[18]	2	3.43506...	Hai moitos outros números da forma${\displaystyle {\sqrt {2k+1}}\ln \left({\frac {{\sqrt {2k+1}}+1}{{\sqrt {2k+1}}-1}}\right)}$ para os que se coñecen límites no seu expoñente de irracionalidade.[18] Este é o caso de ${\displaystyle k=12}$.
${\displaystyle \pi /{\sqrt {3}}}$[19][20]	2	4.60105...	Hai moitos outros números da forma ${\displaystyle {\sqrt {2k-1}}\arctan \left({\frac {\sqrt {2k-1}}{k-1}}\right)}$ para os que se coñecen límites no seu expoñente de irracionalidade.[19] Este é o caso de ${\displaystyle k=2}$.
${\displaystyle \pi }$[12][21]	2	7.10320...	Probouse que se a Serie Flint Hills ${\displaystyle \displaystyle \sum _{n=1}^{\infty }{\frac {\csc ^{2}n}{n^{3}}}}$ (onde n está en radiáns) converxe daquela o expoñente de irracionalidade de ${\displaystyle \pi }$ é como moito ${\displaystyle 5/2}$[22][23] e que se diverxe o expoñente de irracionalidade é como mínimo ${\displaystyle 5/2}$.[24]
${\displaystyle \pi ^{2}}$[12][25]	2	5.09541...	${\displaystyle \pi ^{2}}$ e ${\displaystyle \zeta (2)}$ son linearmente dependentes sobre ${\displaystyle \mathbb {Q} }$.
${\displaystyle \arctan(1/2)}$[26]	2	9.27204...	Hai moitos outros números da forma ${\displaystyle \arctan(1/k)}$ para os que se coñecen límites no seu expoñente de irracionalidade.[27][28]
${\displaystyle \arctan(1/3)}$[29]	2	5.94202...
Constante de Apéry ${\displaystyle \zeta (3)}$[12]	2	5.51389...
${\displaystyle \Gamma (1/4)}$[30]	2	10330
Constante de Cahen ${\displaystyle C}$[31]	3
Constante de Champernowne ${\displaystyle C_{b}}$ ien base ${\displaystyle b\geq 2}$[32]	${\displaystyle b}$		Examplos inclúen ${\displaystyle C_{10}=0.1234567891011...=[0;8,9,1,149083,1,...]}$
Números de Liouville ${\displaystyle L}$	${\displaystyle \infty }$		Os números de Liouville son precisamente aqueles números que teñen un expoñente de irracionalidade infinito.[2]:248

Relación coa converxencia dalgunhas series

Artigo principal: serie Flint Hills.

A serie Flint Hills está definida polo sumatorio:

${\displaystyle S_{1}=\sum _{k=1}^{\infty }{\dfrac {\csc ^{2}{n}}{n^{3}}}}$^[33]

que ven sendo o mesmo que

${\displaystyle S_{1}=\sum _{k=1}^{\infty }{\dfrac {1}{n^{3}\sin ^{2}{n}}}}$^[34].

Non se sabe se esta serie converxe, xa que ${\displaystyle csc^{2}{n}}$ pode ter esporadicamente valores grandes. Os valores de n que fan grande esa función son precisamente os numeradores dos converxentes da fracción continua de ${\displaystyle \pi }$ (secuencia A046947 na OEIS).

Alekseyev (2011)^[35] demostrou que a cuestión da converxencia da serie Flint Hill está relacionada coa medida da irracionalidade de ${\displaystyle \pi }$, e en particular, a converxencia implicaría ${\displaystyle \mu (\pi )<=2.5}$, que é moito máis forte que o mellor límite superior coñecido na actualidade.