Tensión mecánica

En física e enxeñaría, denomínase tensión mecánica ao valor da distribución de forzas por unidade de área no contorno dun punto material dentro dun corpo ou medio continuo.

Para outras páxinas con títulos homónimos véxase: Tensión.

Figure 1  Tensor de tensións

Un caso particular é o da tensión uniaxial, que se define nunha situación en que se aplica forza F uniformemente distribuída sobre unha área A. Nese caso a tensión mecánica uniaxial represéntase por un escalar designado coa letra grega σ (sigma) e vén dada por:

${\displaystyle \sigma ={\frac {F}{A}}}$

Sendo as unidades [Pa] (pascal = [N/m²]), [MPa] = 106 [Pa] (e tamén [kp/cm²]).

A situación anterior pode estenderse a situacións máis complicadas con forzas non distribuídas uniformemente no interior dun corpo de xeometría máis ou menos complexa. Nese caso a tensión mecánica non pode ser representada por un escalar.

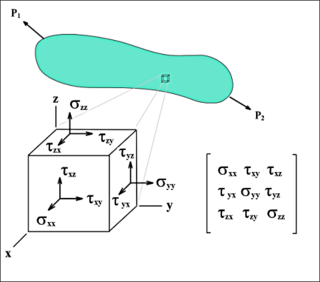
Se se considera un corpo sometido a tensión e imaxina un corte mediante un plano imaxinario π que o divida en dous, sobre cada punto do plano de corte pódese definir un vector tensión tπ que depende do estado tensional interno do corpo, das coordenadas do punto escolleito e do vector unitario normal nπ ao plano π. Nese caso pódese probar que tπ e nπ están relacionados por unha aplicación lineal T ou campo tensorial chamado tensor tensión:

${\displaystyle {t_{\pi }}={T(n_{\pi })}\,}$

Tensión uniaxial (problemas unidimensionais)

A idea orixinal de tensión orixinouse en dúas simples observacións sobre o comportamento de fíos de aceiro:

1. Cando un cable se estira baixo a acción dunha forza F, para valores debaixo de certo límite F < Fc, obsérvase que o alongamento ΔL é proporcional á carga F dividida pola área da sección transversal A do cable. Se se definía s = F/A, o alongamento ΔL era proporcional a σ: ΔL= k·s..
2. O fallo resistente do fío ocorría cando a carga F superaba un certo valor Fc que dependía do material do cabo e da área da sección transversal: Fc = σt A.

Estas observacións suxerían que a característica fundamental que afecta á deformación e o fallo da resistencia dos materiais é a magnitude s, que se chamou tensión. Medidas máis precisas fixeron notar que a proporcionalidade entre tensión e o alongamento non era exacta porque durante o estiramento do fío a sección sufría un estreitamento, polo que A diminuía lixeiramente. Con todo, se se definía a tensión real σ = F/A' onde A' representa agora a área verdadeira baixo a deformación, entón observábase unha proporcionalidade perfecta para valores pequenos de F.

O coeficiente de Poisson introduciuse para dar conta da relación entre a área inicial A e a área deformada A' . A introdución do coeficiente de Poisson nos cálculos estimaba correctamente a tensión ao ter en conta que a forza F distribuíase nunha área algo máis pequena que a sección inicial, o cal fai que σ > s.

Tensión normal e tensión tanxencial

Se nos fixamos nun punto concreto dun corpo sometido a tensión e imaxinamos un corte mediante un plano imaxinario π que o divida en dous, queda definido un vector tensión tπ que depende do estado tensional interno do corpo, das coordenadas do punto escolleito e do vector unitario normal nπ ao plano π definida mediante o tensor tensión:

${\displaystyle {\mathbf {t} _{\pi }}={T(\mathbf {n} _{\pi })}\,}$

Usualmente ese vector pode descomporse en dous compoñentes que fisicamente producen efectos diferentes segundo o material sexa máis dúctil ou máis fráxil. Eses dous compoñentes chámanse compoñentes intrínsecos do vector tensión respecto ao plano π e chámanse tensión normal ou perpendicular ao plano e tensión tanxencial ou rasante ao plano. Estes compoñentes veñen dados por:

${\displaystyle {\begin{cases}\sigma _{\pi }=\mathbf {t} _{\pi }\cdot \mathbf {n} _{\pi }\\\tau _{\pi }=||\mathbf {t} _{\pi }\times \mathbf {n} _{\pi }||\end{cases}}\Rightarrow \qquad ||\mathbf {t} _{\pi }||^{2}=\sigma _{\pi }^{2}+\tau _{\pi }^{2}}$

Analogamente cando existen dous sólidos en contacto e examínanse as tensións entre dous puntos dos dous sólidos, pódese facer a descomposición anterior da tensión de contacto segundo o plano tanxente ás superficies de ambos os sólidos, nese caso a tensión normal ten que ver coa presión perpendicular á superficie e a tensión tanxencial ten que ver coas forzas de fricción entre ambos.

Bibliografía

• Luis Ortiz Berrocal: Resistencia de materiales, Ed. McGraw-Hill/Interamericana de España, Madrid, 1990.
• Dietrich Braess: Finite Element, pp. 250–251, Cambridge University Press, Cambridge UK, 1997.

Véxase tamén

Outros artigos

• Tensor tensión
• Tensor deformación
• Deformación

Ligazóns externas

• Artigos sobre tensión en inglés por Andrés Melo e Geraint Wiggins, formato .PDF