Triángulo isóscele

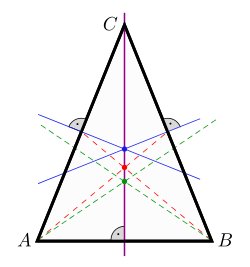
En xeometría, un triángulo isóscele^[1] é un triángulo que ten polo menos dous lados de igual lonxitude. Máis precisamente, dise que un triángulo ABC é isóscele en A cando as lonxitudes AB e AC son iguais. A é entón o vértice principal do triángulo e [BC] a súa base.

Triángulo isóscele
Subclase de	triángulo
Oposto a	triángulo escaleno
Dual de	triángulo escaleno
Facetas do polítopo	aresta
Caracterizado por  área
Composto por  altura  aresta
Fontes e ligazóns
MathWorld	IsoscelesTriangle
OpenAlex	C98653994
[ Wikidata ] [ C:Commons ]

Nun triángulo isósceles, os ángulos adxacentes á base son iguais.

Un triángulo equilátero é un caso particular de triángulo isóscele, que ten os seus tres lados da mesma lonxitude.

Etimoloxía

A palabra "isóscele" provén do grego iso que significa "mesmo" e skelos, "pernas" (o debuxo dun triángulo isóscele pode traer á memoria as dúas patas dun debuxo dun "home").

Propiedades

• Os ángulos da base dun triángulo isóscele son iguais. E viceversa, calquera triángulo con dous ángulos iguais é isóscele.
• Nun triángulo isóscele ABC en A, combínanse a mediana, a altura e a mediatriz procedentes de A, así como a mediatriz da base [BC]. Esta liña é tamén un eixe de simetría do triángulo (e o único, a non ser que o triángulo sexa equilátero).
• O centro da círcunferencia circunscrita dun triángulo agudo descompono en tres triángulos isóscele. O dun triángulo rectángulo (que é o punto medio da hipotenusa) descompono en dous triángulos isósceles.

Triángulos isósceles especiais

Triángulo isóscele rectángulo

Tres cadrados inscritos congruentes no triángulo de Calabi

Un triángulo de ouro subdividido noutro triángulo de ouro menor e nun gnomon de ouro

O Mosaico triangular triaquis

Fórmulas

Nun triángulo isóscele, se denotamos ${\displaystyle a}$ a lonxitude dos dous lados iguais e ${\displaystyle b}$ a lonxitude da base, daquela:

• a lonxitude da altura vén dada pola fórmula : ${\displaystyle h={\sqrt {a^{2}-{\frac {b^{2}}{4}}}}}$ .
• a área do triángulo é ${\displaystyle {\mathcal {A}}={\frac {b}{2}}{\sqrt {a^{2}-{\frac {b^{2}}{4}}}}={\frac {b}{4}}{\sqrt {4a^{2}-b^{2}}}}$ .
• o perímetro do triángulo é ${\displaystyle p=2a+b}$ .

Casos particulares

• Dous triángulos planos poden considerarse isósceles cun ángulo principal de 0° ou 180°.
• O triángulo equilátero é un triángulo isóscele en cada un dos seus vértices, con ángulos de 60°.
• O triángulo rectángulo isósceles tamén se denomina medio cadrado cun ángulo principal de 90°.
• O triángulo áureo (a lonxitude do lado duplicado está na proporción do número áureo en relación á lonxitude do lado distinto), cun ángulo principal de 36° e o gnomon áureo (cun ángulo principal de 108°) aparecen na construción do pentágono regular e nos mosaicos de Penrose.
• O triángulo isóscele cun ángulo principal de 120° está asociado ao mosaico triakis, dobre do mosaico hexagonal truncado.

Caracterización polas lonxitudes de dúas medianas, dúas alturas ou dúas mediatrices

Un triángulo é isóscele se e só se ten dúas medianas (segmentos) ou dúas alturas (segmentos) ou dúas mediatrices (segmentos) da mesma lonxitude.

Os sentidos directos son obvios, e os recíprocos pódense demostrar mediante as expresións das lonxitudes das cevianas dadas polo teorema de Stewart.

Para a igualdade dos segmentos procedentes de A e B, obtemos, coas notacións clásicas do triángulo :

• ${\displaystyle {\frac {a^{2}+c^{2}}{2}}-{b^{2} \over 4}={\frac {a^{2}+b^{2}}{2}}-{c^{2} \over 4}}$ pola igualdade das medianas
• ${\displaystyle {\frac {2}{b}}{\sqrt {p(p-a)(p-b)(p-c)}}={\frac {2}{c}}{\sqrt {p(p-a)(p-b)(p-c)}}}$ pola igualdade das alturas
• ${\displaystyle {\frac {4ac(p-b)p}{(a+c)^{2}}}={\frac {4ab(p-c)p}{(a+b)^{2}}}}$ pola igualdade das mediatrices

que dan en cada caso ${\displaystyle b=c}$ ^[2].

Tamén atoparemos en Ladegaillerie 2003, p. 330 , unha demostración xeométrica para as bisectrices.

Figuras en tres dimensións

Sólidos de Catalan con caras triangulares isósceles

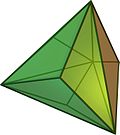
Triaquistetraedro

Triaquisoctaedro

Tetraquishexaedro

Pentaquisdodecaedro

Triaquisicosaedro

Cinco sólidos de Catalan (triaquistetraedro, triaquisoctaedro, tetraquishexaedro, pentaquisdodecaedro e triaquisicosaedro), teñen caras que son triángulos isósceles.