אי-שוויון המשולש

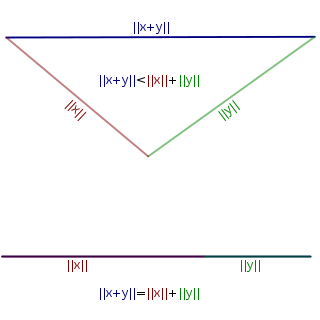
במתמטיקה, אי-שוויון המשולש הוא אי-שוויון מהצורה ${\displaystyle \ d(A,C)\leq d(A,B)+d(B,C)}$, כאשר ${\displaystyle \ d(\cdot ,\cdot )}$ היא פונקציית מרחק. אי-השוויון מתאר את העובדה הגאומטרית שהקו הישר הוא הדרך הקצרה ביותר בין שתי נקודות; בפרט, אורכה של צלע במשולש אינו עולה על סכום אורכי הצלעות האחרות. אי-שוויון המשולש נחשב לתכונה יסודית של כל שיטה למדידת מרחק, ומשום כך מניחים, כאקסיומה, שהוא מתקיים בכל מרחב מטרי או נורמי. הגרסה החזקה ${\displaystyle \ d(A,C)\leq \max\{d(A,B),d(B,C)\}}$ נקראת אי-שוויון המשולש למטריקות לא ארכימדיות.

אי-שוויון המשולש בין מספרים ממשיים

ניתן לראות את אי-שוויון המשולש במספרים הממשיים כמקרה פרטי של אי-השוויון על הישר הממשי. כיוון שהמרחק בין שתי נקודות על הישר נמדד באמצעות הערך המוחלט, אי-השוויון במקרה זה שקול ל-${\displaystyle \ |a-c|\leq |a-b|+|b-c|}$, לכל ${\displaystyle \ a,b,c\in R}$.

כשבוחרים c=0, b=y ו-a=x+y, מתקבלת הצורה החלופית ${\displaystyle \ |x+y|\leq |x|+|y|}$. צורה זו אפשר להוכיח בעזרת חיבור שני האי-שוויונים ${\displaystyle \ -|x|\leq x\leq |x|}$ ו-${\displaystyle \ -|y|\leq y\leq |y|}$, או בדיקה של האפשרויות השונות לסימנים של x ושל y.

גרסה נוספת של אי-שוויון המשולש היא: ${\displaystyle {\bigg |}|x|-|y|{\bigg |}\leq |x-y|}$.

הוכחה פורמלית

לצורך הוכחת אי השוויון נשתמש בתכונות ${\displaystyle \ |a|=|-a|}$ ו-${\displaystyle \ a\leq |a|}$. אם ${\displaystyle \ x+y\geq 0}$ אז ${\displaystyle \ |x+y|=x+y\leq |x|+|y|}$. אחרת, ${\displaystyle \ x+y<0}$ ומכאן ${\displaystyle \ |x+y|=-x-y\leq |-x|+|-y|=|x|+|y|}$ ולכן ${\displaystyle \ |x+y|\leq |x|+|y|}$.

דרך נוספת היא להשתמש בשוויון ${\displaystyle \ |a|=\max\{a,-a\}}$, ואז ${\displaystyle \ |x+y|=\max\{x+y,-x-y\}\leq \max\{|x|+|y|,|-x|+|-y|\}=\max\{|x|+|y|,|x|+|y|\}=|y|+|x|}$.

הוכחה של ${\displaystyle {\bigg |}|x|-|y|{\bigg |}\leq |x-y|}$:

לפי אי שוויון המשולש ${\displaystyle |x|=|(x-y)+y|\leq |x-y|+|y|}$ ולכן ${\displaystyle |x|-|y|\leq |x-y|}$

וגם ${\displaystyle |y|=|(y-x)+x|\leq |y-x|+|x|}$ ולכן ${\displaystyle -(|x|-|y|)=|y|-|x|\leq |y-x|=|x-y|}$

ולכן לפי ש ${\displaystyle |x|-|y|\leq |x-y|}$ וגם ${\displaystyle -(|x|-|y|)\leq |x-y|}$ אז ${\displaystyle {\bigg |}|x|-|y|{\bigg |}\leq |x-y|}$

המקרה המרוכב

אי-שוויון המשולש במישור המרוכב הוא הטענה ${\displaystyle \ |x+y|\leq |x|+|y|}$, המתייחסת למספרים מרוכבים. ניתן להוכיח את נכונותו שם בכמה דרכים: גאומטרית, הוא שקול לתכונות היסוד של משולש; אלגברית, אפשר לקבל אותו על ידי העברת אגפים מתאימה והעלאה בריבוע; וניתן להסיק אותו מאי-השוויון הממשי באמצעות משפט פיתגורס.

אי-שוויון המשולש במרחבים מופשטים

אי-שוויון המשולש מבטא את העובדה שלא ניתן לקצר את הדרך מ-A ל-C על ידי מעבר בנקודה B. זוהי תכונה יסודית כל-כך של מושג ה"מרחק", עד שהיא מהווה אחת מהאקסיומות המגדירות מטריקה ומרחב מטרי. מאותה סיבה, מניחים את האקסיומה ${\displaystyle \ \|x+y\|\leq \|x\|+\|y\|}$ בהגדרה של נורמה ומרחב נורמי.

ראו גם

• אי-שוויון המשולש האינטגרלי

קישורים חיצוניים

מדיה וקבצים בנושא אי-שוויון המשולש בוויקישיתוף

• אי-שוויון המשולש, באתר MathWorld (באנגלית)
• אי-שוויון המשולש, באתר אנציקלופדיה בריטניקה (באנגלית)