Epicicloide

In geometria, un'epicicloide è una curva piana appartenente alla categoria delle rullette, ovvero delle curve generate da un punto di una figura che rotola su un'altra. L'epicicloide infatti è definita come la curva generata da un punto di una circonferenza che rotola sulla superficie esterna di un'altra circonferenza. L'epicicloide può essere vista come un caso particolare dell'epitrocoide. Questo termine viene anche utilizzato per indicare la curva che la Luna descrive intorno al Sole nel suo moto di traslazione; essa interseca il piano orbitale terrestre ben 24-25 volte all'anno ed è sempre concavo verso il sole.

La curva rossa è un'epicicloide tracciata facendo ruotare il cerchio nero, di raggio r = 1, attorno ed esternamente al cerchio blu, di raggio R = 3.

Epicicloide a tre cuspidi generata da una circonferenza di raggio 2 che rotola su una circonferenza di raggio 3.

L'epicicloide è un caso speciale di epitrocoide.

La cardioide è un tipo particolare di epicicloide con una sola cuspide.

Un'epicicloide e la sua evoluta sono simili.

Forma matematica

La rappresentazione parametrica di un'epicicloide generata da una circonferenza di raggio ${\displaystyle r}$ che rotola su una circonferenza più grande di raggio ${\displaystyle R=kr}$ è data da

${\displaystyle {\begin{cases}x(\theta )=\left(R+r\right)\cos \theta -r\cos \left({\frac {R+r}{r}}\theta \right)\\y(\theta )=\left(R+r\right)\sin \theta -r\sin \left({\frac {R+r}{r}}\theta \right)\end{cases}}}$

oppure

${\displaystyle {\begin{cases}x(\theta )=r(k+1)\cos \theta -r\cos \left((k+1)\theta \right)\\y(\theta )=r(k+1)\sin \theta -r\sin \left((k+1)\theta \right)\end{cases}}}$

L'epicicloide è una funzione continua ed è differenziabile ovunque, tranne che sulle cuspidi. Dalle equazioni parametriche si può notare con facilità che per ${\displaystyle k\in \mathbb {N} ^{*}}$ (l'insieme dei numeri naturali senza lo zero) la velocità del punto che descrive l'epicicloide nei punti di cuspide (che appartengono sia alla circonferenza che rotola e quella fissa) è nulla: proprio la condizione che soddisfa il moto di puro rotolamento (questo vale naturalmente per tutti i punti della circonferenza che rotola).

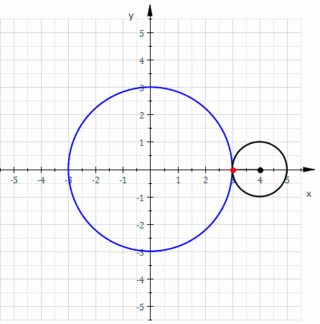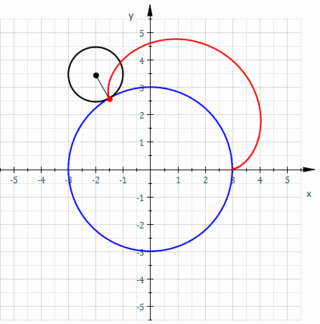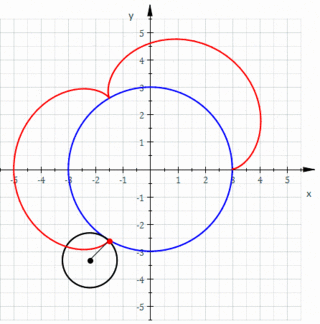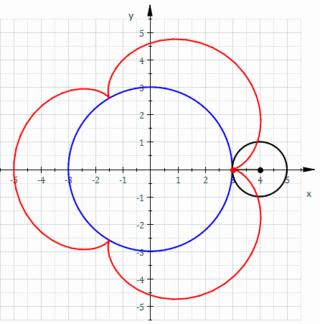
Esempi di epicicloidi

• 
  k = 1
• 
  k = 2
• 
  k = 3
• 
  k = 4
• 
  k = 2,1 = 21/10
• 
  k = 3,8 = 19/5
• 
  k = 5,5 = 11/2
• 
  k = 7,2 = 36/5

Dimostrazione

Facendo riferimento all'immagine a fianco, ipotizziamo di voler determinare la posizione di ${\displaystyle p}$. Siano ${\displaystyle \alpha }$ i radianti dell'arco che ha per estremi il punto di tangenza e il punto mobile ${\displaystyle p}$, e ${\displaystyle \theta }$ i radianti dell'arco che ha per estremi l'intersezione del cerchio maggiore col semiasse ${\displaystyle x}$ positivo e il punto di tangenza.

Dal momento che non c'è alcuno scorrimento tra le due circonferenze, abbiamo che

${\displaystyle \ell _{R}=\ell _{r}.}$

Dalla definizione di radiante (rapporto tra arco e raggio), abbiamo che

${\displaystyle \ell _{R}=\theta R,\ell _{r}=\alpha r.}$

Dalla due condizioni, otteniamo l'identità

${\displaystyle \theta R=\alpha r.}$

Pertanto, la relazione tra ${\displaystyle \alpha }$ e ${\displaystyle \theta }$ è

${\displaystyle \alpha ={\frac {R}{r}}\theta .}$

A questo punto, osservando la figura, la posizione di ${\displaystyle p}$ si ricava facilmente:

${\displaystyle x=\left(R+r\right)\cos \theta -r\cos \left(\theta +\alpha \right)=\left(R+r\right)\cos \theta -r\cos \left({\frac {R+r}{r}}\theta \right)}$

${\displaystyle y=\left(R+r\right)\sin \theta -r\sin \left(\theta +\alpha \right)=\left(R+r\right)\sin \theta -r\sin \left({\frac {R+r}{r}}\theta \right).}$

Voci correlate

• Epitrocoide
• Rulletta
• Cicloide
• Ipocicloide
• Epiciclo e deferente
• Spirograph

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file su epicicloide

Collegamenti esterni

• (EN) Eric W. Weisstein, Epicycloid, su MathWorld, Wolfram Research.
• (EN) Epicicloide, su Encyclopaedia of Mathematics, Springer e European Mathematical Society.

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica