Teorema dei seni

In trigonometria, il teorema dei seni (noto anche come teorema di Eulero) esprime una relazione di proporzionalità diretta fra le lunghezze dei lati di un triangolo e i seni dei rispettivi angoli opposti.

Un triangolo generico con le comuni notazioni

Si consideri il triangolo generico ABC rappresentato nella figura a lato, in cui gli angoli sono indicati da lettere greche minuscole e i lati opposti agli angoli dalle corrispondenti lettere latine minuscole.

${\displaystyle a={\overline {BC}},~~\alpha =C{\hat {A}}B}$

${\displaystyle b={\overline {AC}},~~\beta =A{\hat {B}}C}$

${\displaystyle c={\overline {AB}},~~\gamma =B{\hat {C}}A}$

Vale quindi

${\displaystyle {\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}={\frac {abc}{2S}}=2R}$

dove R è il raggio del cerchio circoscritto al triangolo ABC e

${\displaystyle S={\sqrt {p(p-a)(p-b)(p-c)}}}$

è l'area del triangolo ricavata dal semiperimetro p grazie alla formula di Erone.

La relazione di proporzionalità viene formulata a volte in questo modo:

${\displaystyle a:b:c=\sin \alpha$ :\sin \beta :\sin \gamma } .

Applicazioni

Risoluzione di un triangolo con il teorema dei seni

Il teorema può essere adoperato

• per determinare il raggio del cerchio circoscritto:

${\displaystyle R={\frac {a}{2\,\sin \alpha }}}$

• per la risoluzione di un triangolo dati un angolo, un lato adiacente all'angolo e il lato opposto (vedere figura a lato):

${\displaystyle \alpha =\mathrm {arcsen} \,{\frac {a\,\sin \beta }{b}}}$.

Generalizzazione alle geometrie non euclidee

Lo stesso argomento in dettaglio: Geometrie non euclidee.

Triangolo sferico: dimensioni ridotte a, b e c; angoli α, β e γ

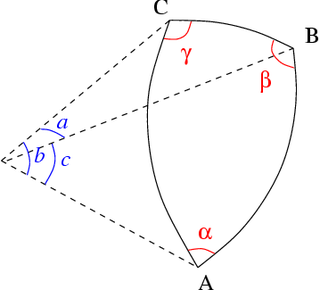
Per una superficie non euclidea dalla curvatura K, il raggio di curvatura ρ è

${\displaystyle \rho =1/{\sqrt {|K|}}}$.

Si definiscono quindi le dimensioni ridotte del triangolo:

${\displaystyle a={\overline {BC}}/\rho }$,

${\displaystyle b={\overline {AC}}/\rho }$,

${\displaystyle c={\overline {AB}}/\rho }$.

Nel caso di un triangolo sferico, a, b e c corrispondono alle misure angolari dei segmenti degli archi grandi [BC], [AC] e [AB] (vedere figura).

Geometria sferica

In un triangolo sferico ABC tracciato sulla sfera di centro O e di raggio ρ, il teorema del seno è espresso da

${\displaystyle {\frac {\sin a}{\sin \alpha }}={\frac {\sin b}{\sin \beta }}={\frac {\sin c}{\sin \gamma }}={\frac {6V_{OABC}}{\rho ^{3}\,\sin a\ \sin b\ \sin c}}}$,

dove V_OABC è il volume del tetraedro OABC.

Geometria iperbolica

Lo stesso argomento in dettaglio: Geometria iperbolica.

In un triangolo iperbolico, il teorema dei seni si esprime con

${\displaystyle {\frac {\mathrm {senh} \,a}{\sin \alpha }}={\frac {\mathrm {senh} \,b}{\sin \beta }}={\frac {\mathrm {senh} \,c}{\sin \gamma }}}$.

Generalizzazione al tridimensionale (euclideo)

Lo stesso argomento in dettaglio: Spazio euclideo.

Tetraedro: facce ed angoli diedri

Si consideri un tetraedro A₁A₂A₃A₄ nello spazio tridimensionale. La figura di lato mostra un tetraedro proiettato su un piano e indica le notazioni di vertici, facce e angoli del tetraedro:

• S_k la faccia opposta al vertice A_k;
• s_k la superficie di S_k;
• Δ_k il piano su cui giace S_k;
• θ_ij l'angolo diedro ${\displaystyle {\widehat {(\Delta _{i},\Delta _{j})}}}$.

Il seno dell'angolo triedro in corrispondenza del vertice A₁ si definisce nel modo seguente:

${\displaystyle \sin A_{1}={\frac {\sqrt {1-\cos ^{2}\theta _{23}-\cos ^{2}\theta _{24}-\cos ^{2}\theta _{34}-2\cos \theta _{23}\cos \theta _{24}\cos \theta _{34}}}{\sin \theta _{23}\ \sin \theta _{24}\ \sin \theta _{34}}}}$;

E in modo analogo per gli altri angoli triedri.

Vale quindi

${\displaystyle {\frac {s_{1}}{\sin A_{1}}}={\frac {s_{2}}{\sin A_{2}}}={\frac {s_{3}}{\sin A_{3}}}={\frac {s_{4}}{\sin A_{4}}}={\frac {2s_{1}s_{2}s_{3}s_{4}}{9V}}}$,

dove V è il volume del tetraedro.

Voci correlate

• Seno (matematica)
• Trigonometria
• Triangolo
• Teorema del coseno
• Teorema della corda

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file sul teorema dei seni

Collegamenti esterni

• seni, teorema dei, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
• (EN) law of sines, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Eric W. Weisstein, Law of Sines, su MathWorld, Wolfram Research.

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica