ハートの反転器

ハートの反転器（ハートのはんてんき、反転機とも^[1]、英: Hart's inversors）は、回転運動を直線運動（英語版）に変換することができる2つの平面機構である^[2][3]。ハリー・ハート（1874 - 1875）によって発明された^[3][4]。

ハートの（第一）反転器のアニメーション。

  クランクと固定点 a

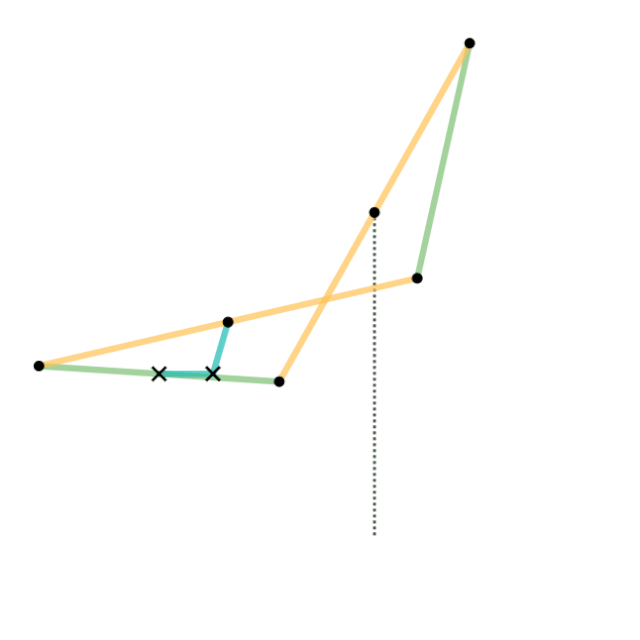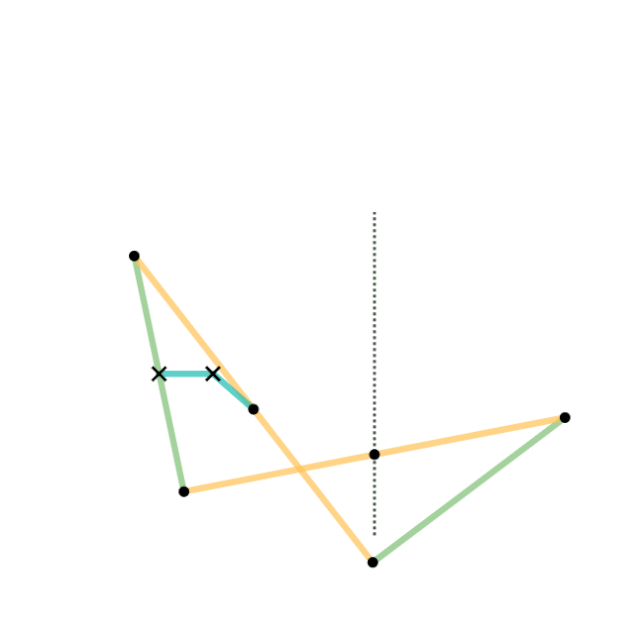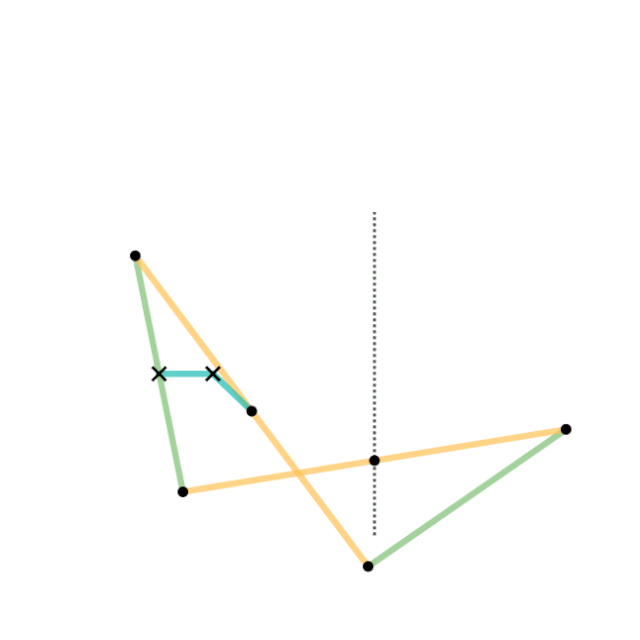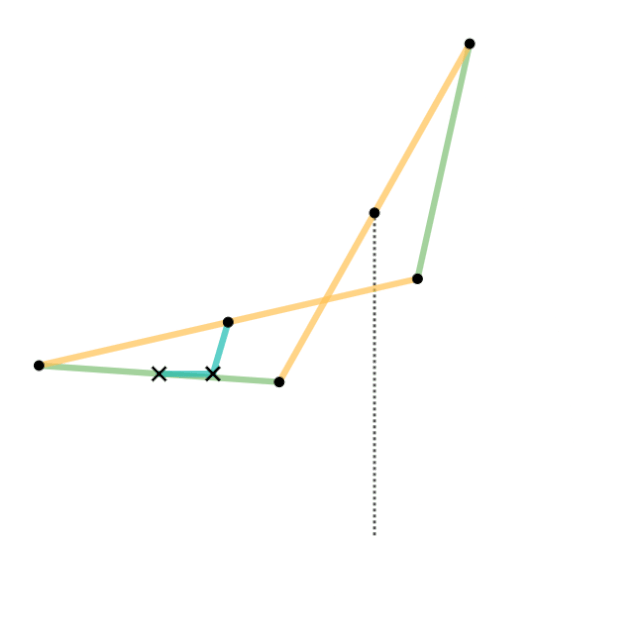
  ロッカー機構 b （中点で固定されている）

  連結器 c （中点で接続されている）

${\displaystyle {\begin{aligned}b&<c\\[4pt]2a&<{\tfrac {1}{2}}b+{\tfrac {1}{2}}c\\[2pt]{\tfrac {1}{2}}c&<{\tfrac {1}{2}}b+2a\end{aligned}}}$

ハートの反転器

ハートの反転器、あるいはハートの直交ガイド^[2]（Hart's first inversor, Hart's W-frame）は交叉平行四辺形（英語版）を基とした、固定点と6つの節からなる機構である。短い節を固定し、その一端につなげた節を回転させることで完璧な直線運動を作りだすことができる^[3][5]。また、点の反転を作図する際にも有用である^[1]。

Rectilinear bar と quadruplanar inversor

→詳細は「Quadruplanar inversor」を参照

ハートの反転器から派生したQuadruplanar inversor（英語版）のアニメーション。

ハートの反転器を改良して、8つのリンケージからなる quadruplanar inversor と呼ばれる機構が開発された。回転移動を節の平行移動に変換することができる。

ジェームス・ジョセフ・シルベスターとアルフレッド・ケンペ（英語版）によって更なる一般化が行われている^[6][7]。

Hart's second inversor

Hart's A-frame のアニメーション。

  二重のロッカー機構 3a + a （アンカー同士の距離は2b）

  連結器 b

  Aの先端 2a

Hart's second inversor（Hart's A-frame）は柔軟性においては劣るものの、固定点の垂直二等分線上の直線運動をもたらす点で有用な性質がある。ローマ文字の A の様な、台形の上に三角形を携えた形をしている。6本の節から成る。

ハートの相似・回転変換器

定点をOとするひし形OABCを作る。更にひし形の外側にBを通りそれぞれA, Cを中心とする半円を作り、そのそれぞれに△BAPと△QCBが順相似となるように点P, Qを取る。APの中点を動かしたとき、CをQで鏡映した点の軌跡は、APの中点の軌跡を∠BAP回転し2倍拡大した図形となる。この機構をハートの相似・回転変換器という^[2]。

例

以下に挙げる例は、アニメーションにある機構で使われた節の長さとなっている。

• 
  • Hart's first inversor:
  • AB = Bg = 2
  • CE = FD = 6
  • CA = AE = 3
  • CD = EF = 12
  • Cp = pD = Eg = gF = 6
• 
  • Hart's second inversor:
  • AB = AC = BD = 4
  • CE = ED = 2
  • Af = Bg = 3
  • fC = gD = 1
  • fg = 2