閉道 (位相幾何学)

数学の特に位相幾何学における閉道（へいどう、英: closed-path）またはループ (loop) は、始点と終点が等しい道を言う^[1]。閉道の始点かつ終点となる点を基点 (basepoint) と呼ぶ^[2]。

トーラスにおける二つの閉道 a, b

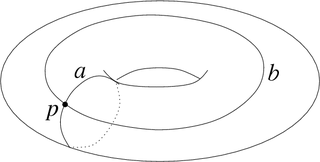
陽に書けば、位相空間 X 内の閉道とは、単位区間 I ≔ [0, 1] から X への連続写像 f で f(0) = f(1) を満たすものである。点付き単位円 S¹ は I の 0 と 1 を等化して得られる商位相空間と見なせるから、X 内の閉道を S¹ から X への連続写像 f のことと定めてもよい。基点 x を持つ閉道の全体は Ω_xX のように書かれる^[3]。X 内の閉道全体の成す集合は、コンパクト開位相を入れて X のループ空間 ΩX と呼ばれる一つの位相空間を成す^[4]。

やや変更して、適当な実数 |f| > 0 に対して閉区間 [0, |f|] を定義域とする連続写像 f: [0, |f|] → X; f(0) = f(|f|) を X 内のムーアループ (Moore loop) と呼ぶ^[5]:44。基点を共有するムーアループの全体は道の合成 (concatenation) に関してモノイドを成す^[6]。

複素解析では求長可能な閉道に興味がもたれる。X ≔ ℂ のとき、閉道 γ に対し、γ の巻き数 (winding number) I(γ, z₀) が各点 z₀ ∈ ℂ ∖ γ([0, 1]) で定義される。これは z₀ の周りを γ が何周するかを表す整数であり、$${\displaystyle I(\gamma ,z_{0}):={\frac {1}{2\pi i}}\int _{\gamma }{\frac {dz}{z-z_{0}}}}$$ で計算できる。

関連項目

• 自由ループ（英語版）: 基点を持たない閉道
• ループ群（英語版）: 位相群上のループ空間が点ごとの積に関してなす群
• ループ空間（英語版）
• ループ代数
• 基本群: 閉道の基点を保つホモトピー類の全体が道の合成に関してなす群