ワイエルシュトラス関数

ワイエルシュトラスのペー関数については「ヴァイエルシュトラスの楕円函数」をご覧ください。

ワイエルシュトラス関数（ワイエルシュトラスかんすう、英: Weierstrass function）は、1872年にカール・ワイエルシュトラスにより提示された実数関数で、連続関数であるにもかかわらず至るところ微分不可能な関数である。病的な関数（英語版）の例として取り上げられることがある。

ワイエルシュトラス関数(区間 [−2, 2])。 この関数はフラクタル挙動を示す: スケールを変えると似た構造が現れる(赤色の円)自己相似性をもつ。

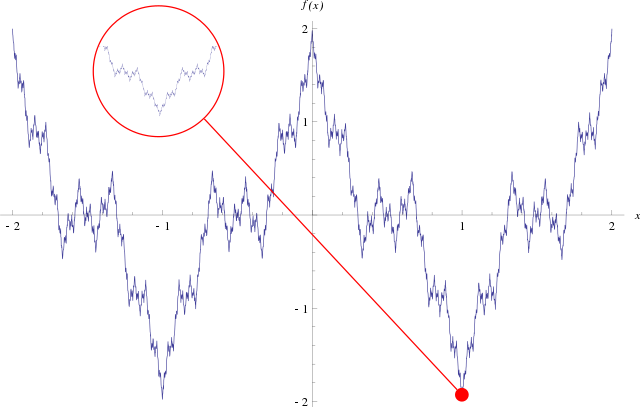
「孤立点を除くと連続関数は微分可能である」という認識を変えた出版された初めての例として、ワイエルシュトラス関数は歴史的に重要である。

ワイエルシュトラス関数

定義

ワイエルシュトラスのオリジナル論文において、この関数は次のように定義される。

${\displaystyle w(x)=\sum _{n=0}^{\infty }a^{n}\cos(b^{n}\pi x).}$

ここで、0 < a < 1, b は正の奇数整数。また、

${\displaystyle ab>1+{\frac {3}{2}}\pi .}$

この定義は、微分不可能であることの証明とともに、1872年7月18日にプロイセン科学アカデミー (Königliche Akademie der Wissenschaften) へ提出された。

ハウスドルフ次元

ハウスドルフ次元は次のとおりとなる^[1]。

${\displaystyle D_{H}=2+{\frac {\log {a}}{\log {b}}}}$

スケール不変性

ワイエルシュトラス関数では和をn ≥ 0 についてのみとるため厳密にはスケール不変とはならない。

${\displaystyle {\begin{aligned}w(bx)&=b^{-1}\sum _{n=0}^{\infty }b^{n+1}\cos {(b^{n+1}\pi x)}\\&=b^{-1}\sum _{n=-1}^{\infty }b^{n+1}\cos {(b^{n+1}\pi x)}-b^{-1}b^{0}\cos(b^{0}\pi x)\\&=b^{-1}\left[w(x)-\cos \pi x\right]\\&\neq b^{-1}w(x)\end{aligned}}}$

したがって、厳密な意味での自己相似性をもたない。

リプシッツ連続性

ワイエルシュトラス関数のリプシッツ定数は無限大である。

ワイエルシュトラス・マンデルブロ関数

ブノワ・マンデルブロは、ワイエルシュトラス関数を一般化した次のワイエルシュトラス・マンデルブロ関数 (英:Weierstrass-Mandelbrot function)を提示^[2]した。

定義

${\displaystyle W(t)=\sum _{n=-\infty }^{\infty }{\frac {(1-e^{i\gamma ^{n}t})e^{i\phi _{n}}}{\gamma ^{(2-D)n}}}}$,

ここで、 1 < D < 2, γ > 1 である。

これは、φ = 0として実部をとるとワイエルシュトラス関数となる。

${\displaystyle \operatorname {Re} W(t)=\sum _{n=-\infty }^{\infty }{\frac {1-\cos(\gamma ^{n}t)}{\gamma ^{(2-D)n}}}}$

フラクタル次元

ハウスドルフ次元は D と考えられているが厳密な証明はなされていない。

スケール不特定の条件下でのみスケール不変となる。

ただし、φ_n = μn、不変となるものを離散的スケール不変性(DSI, Discrete Scale Invariance)という。

統計的性質

• アンサンブル平均はゼロ ${\displaystyle \langle W(t+\tau )-W(t)\rangle _{e}=0}$
• 分散はγについてのみスケール不変となる。

${\displaystyle {\begin{aligned}V(\tau )&=\langle W(t+\tau )-W(t)\rangle _{e}=2\sum _{n=-\infty }^{\infty }{\frac {1-\cos(\gamma ^{n}\tau )}{\gamma ^{(4-2D)n}}},\\V(\gamma \tau )&=\gamma ^{4-2D}V(\tau )\end{aligned}}}$

パワースペクトル

パワースペクトルはおおよそ次の近似式で表すことができる。

${\displaystyle S(\omega )\approx {\frac {1}{\omega ^{5-2D}\log {\gamma }}}}$

すなわち、D → 2 のとき1/fゆらぎに近づく。

ワイエルシュトラス・マンデルブロ関数の一般化

ワイエルシュトラス・マンデルブロ関数(WMF)は、次のようにさらに一般化することができる^[3]。

${\displaystyle W_{g}(t)=\sum _{n=-\infty }^{\infty }\lambda ^{-nH}(g(0)-g(\lambda ^{n}t))e^{i\phi _{n}}}$,

ここで、H < 1、g (t) は t = 0 で微分可能な周期関数。