トップQs
タイムライン
チャット
視点
完全微分
ウィキペディアから
Remove ads
完全微分(かんぜんびぶん、英: exact differential)とは、関数の全微分として書ける1次の微分形式の事で、多様体論などの数学の分野では(1次の)完全形式と呼ばれる。本項では主に物理学に応用する事を想定して直観的に完全微分を説明する。より厳密な取り扱いは微分形式、外微分等の項目を参照されたい。
概要
要約
視点
定義
→詳細は「§ 定義の節」を参照
線積分
の「中身」である
を1次の微分形式といい[注 1]、1次の微分形式の中で特に何らかの関数の全微分
の形に書けるものを完全微分、そうでないものを不完全微分という。
ある微分形式が完全微分であるか否かは座標系によらない。すなわち、ある座標系で完全微分、不完全微分なものはそれぞれ、別の座標系でも完全微分、不完全微分である(詳細)。
不完全微分の表記
→詳細は「§ 表記の節」を参照
不完全微分の線積分が物理量を表しているとき、その「中身」である不完全微分を
のように表す。「」は全微分と区別するための「単なる記号」[1]であり、完全微分と区別する以上の意味はなく[1]、が具体的になにかの関数の全微分になっている事を意味するわけではない。
性質
微分形式が完全微分である必要十分条件は、線積分が経路に依存しない事である(詳細)。
簡単な計算から、微分形式が完全微分であれば、
- for
を満たす事が確かめられる。逆に微分形式が上式を満たすと、を満たすが局所的に存在する事が示せるが(詳細)、一般には大域的に存在するとは限らない。
具体例
→詳細は「§ 具体例の節」を参照
熱力学において、温度、圧力、体積などは完全微分の積分によって記述できる。一方力学的仕事は不完全微分の積分として記述される。よって力学的仕事の値は積分経路に依存する。
Remove ads
定義と基本的な性質
要約
視点
定義
直観的な定義 (微分形式) ― Mをn次元ユークリッド空間の領域、をの座標(あるいはより一般にMを滑らかな多様体、をMの滑らかな局所座標[注 2])とする。滑らかな関数と「微小量」、を用いて
- ...(1)
定義 (完全微分、不完全微分) ― 何らかの滑らかな関数の全微分
- ...(2)
の形にかける1次の微分形式(すなわちが任意のiに対して成り立つAが存在する微分形式)を完全微分(英: exact differential[2], perfect differential)といい[3]、をこの完全微分のポテンシャル(英: potential)という[3]。
1次の微分形式で、完全微分でないものを不完全微分(英: imperfect differential[2][4])という。
なお、滑らかな関数Aに対し、全微分をAの微分形という。 完全微分のポテンシャルは微分積分学の基本定理より定数項を除いて一意である[2]。すなわち、ならを満たす定数が存在する[注 3]。
以上の概念は数学と物理学で名称が異なるので、下記のように表でまとめた:
座標変換に対する不変性
M上に(あるいはより一般にMの開集合上に)2つの座標系、が定義されているとき、で表記された微分形式
- ...(A)
のを(をの関数とみなしたときの)全微分
に置き換える事でで表記された微分形式
- ...(B)
に変換できる。ここではを座標で表したものである。(A)と(B)は異なる座標系、で表示された同一の微分形式であるとみなす。
全微分は座標変換に対して自然に振る舞う:
定理 ― 座標系で表された滑らかな関数を全微分してから座標系 に変数変換したものは、を座標系 に変数変換したを全微分したものと一致する [注 4]。
証明
よって特に完全微分の概念は座標変換に対して不変である:
系 (完全微分の概念の座標不変性) ― 座標系で表記された(A)の微分形式が完全微分である必要十分条件はこの微分形式を座標系で表した(B)の微分形式が完全微分である事である。
証明
(A)が完全微分であれば、
を満たす滑らかな関数が存在する。
とすれば、上記の定理より、は(B)に一致する。
逆向きの変数変換に対して同様の証明をすれば十分性も従う。
上記の定理により、「この微分形式は完全微分である」というとき、どの座標系にとって完全微分であるかを問わなくて良い。後述するように完全微分の概念は熱力学に応用を持つが、熱力学で完全微分の議論をする際、それがSVN座標に対してなのかUVN座標に対してなのかを明示する必要がないのはこの定理があるためである。
完全微分、不完全微分の表記
数学では(1)の(完全微分もしくは不完全微分の)微分形式を
のようにやといったギリシア文字で表す事が多い。が完全微分であれば、
のようにポテンシャルの全微分としても表記できるが、が不完全微分の場合にはこれに類似した表記はない。
一方物理学では不完全微分に対する表記方法も用意している。物理学では(1)を与えられた曲線γに沿って線積分した
- ...(3)
が何らかの物理量を表している事が多く、(1)の形の不完全微分を(3)のように線積分したものが物理量Bを表しているとき、(1)を
のように表す。教科書によっては「」[5]、「」[1]と表記するものもある。
「」は全微分と区別するための「単なる記号」[1]であり、完全微分と区別する以上の意味はなく[1]、が具体的になにかの関数の全微分になっている事を意味するわけではない。実際、一般には(3)の線積分は経路に依存するため、物理量はに実数を対応させる関数にはならず、各経路に実数を対応させる関数になってしまう。
次節で述べるように、がに実数を対応させる関数になる必要十分条件は(1)の微分形式が完全微分な事である。
完全微分と経路非依存性
定理 ― 以下の2つは同値である[6]:
- (3)の線積分は経路γに依存せず、γの始点と終点のみで決まる。
- (1)の微分形式は完全微分である
証明
(1)の微分形式を以下ωと書く。
() ωは完全微分なので、
を満たす滑らかな関数が存在する。したがって微分積分学の基本定理により、
となり始点0と終点1のみに依存する。
() 点をfixする。に対し、とをつなぐ曲線を取り[注 5]
と定義すると、仮定からはγの取り方によらずwell-definedである。
、 と成分で表し、、 からへ行く曲線を任意に取り、を曲線
とすると、
が成立する。同様の議論により
が任意のiについて示せるので定理が証明された。
(1)の微分形式が完全微分なら、(3)の線積分が経路に依存しないので、基点を固定し、
という(経路に依存せず、基点と終点だけに依存する)物理量を定める事ができる。そして上記のAを全微分したが(1)の微分形式に一致する。なお前述のように、が(1)の微分形式と一致するAは定数項を除いて一意である。
具体例
熱力学ではMは熱力学的な「平衡状態」の空間であり[7]、具体的には物理的な系の内部エネルギー、体積、物質量(=モル数)といった変数で記述される空間である[注 6][注 7]。
完全微分として表せる量としては温度、圧力、体積などがある。温度は平衡状態に実数を対応させる関数
として定式化できる量であり、したがってその全微分(これは定義により完全微分)の線積分
としても書ける。そしてこの線積分の結果は経路によらず、の終点のみで決まるである[注 8]。
一方、不完全微分で記述される物理量の具体例としては力学的仕事がある。をの各点が表す平衡状態の圧力および体積とするとき、力学的仕事は不完全微分
を線積分した
の形で定式化される。よってM上でどのような経路をたどったかによって力学的仕事は異なってしまう[8]。
熱力学では平衡状態に実数を対応させる関数として定式化できる物理量を状態量と呼ぶ。よって温度は状態量だが力学的仕事は状態量ではない。上述の定理より、(1)の微分形式が完全微分か否かは、(3)の線積分の結果得られる物理量が状態量であるか否かを特徴づける事になる。
ポアンカレの補題
以上で説明したように、微分形式が完全微分か否かは物理的に重要な意味を持つため、本節では微分形式が完全微分であるための条件を見る。
を微分形式とするとき、が完全微分であれば、となるが存在し、を満たすので、となる。したがって
- for
はωが完全微分であるための必要条件となる。
逆に上記の条件が成立してもとなるがMの全域で定義された(一価の[注 9])関数として存在するとは限らない。しかし上記の条件を満たせば局所的にはそのようなが存在する事が知られている:
に対し、以下の2つは同値である:
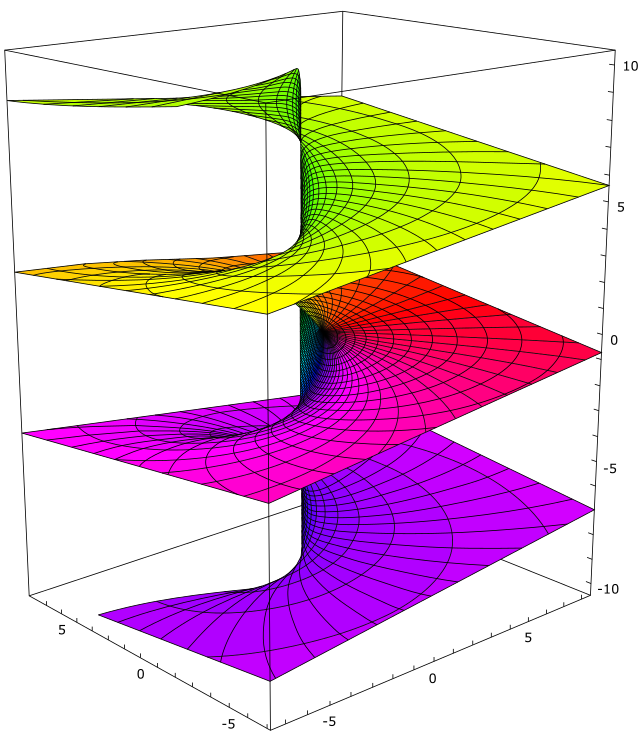
実際、を極座標表示に変換すると、と書ける事から、のポテンシャルは点にを対応させる関数となるので、 ()分の多価性がある。
一般には上記の定義で局所的に存在を保証されたAをMの全域に拡張しようとすると、Aは多価関数になってしまう。
例えばが原点以外の2次元平面で定義されているとき[注 11]には原点の周りを「右回り」の曲線に沿ってAを拡張したのか、「左回り」の曲線に沿ってAを拡張したかによってAの値は変わってしまう場合がある(右図)。同様にMがトーラスであればトーラスの周りを「右回り」にAを拡張したのか、「左回り」に拡張したかによってAの値は変わってしまう場合がある。
Mが単連結であれば(あるいはより一般に1次のコホモロジー群が0であれば)、このような多価性の問題は生じず、AをMの全域に拡張できる。詳細はド・ラームコホモロジーの項目を参照されたい。
Remove ads
偏微分関係式
要約
視点
三次元空間上の定義された滑らかな実数値関数により定義される曲面
を考える。上述の曲面上の点に対し、であれば、陰関数定理よりをについて解いた
をの近傍で定義できる。同様に、であれば、
もの近傍で定義可能である。
証明
輪環関係式は三重積の微分法則とも呼ばれる。
相反関係式は変数をサイクリックに入れ替えた
も成立する。
Remove ads
関連項目
脚注
参考文献
外部リンク
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads












































































































![{\displaystyle {\begin{aligned}{\mathit {dx}}&=\left({\frac {\partial x}{\partial y}}\right)_{z}\mathrm {d} y+\left({\frac {\partial x}{\partial z}}\right)_{y}\mathrm {d} z,\\[5pt]{\mathit {dz}}&=\left({\frac {\partial z}{\partial x}}\right)_{y}\mathrm {d} x+\left({\frac {\partial z}{\partial y}}\right)_{x}\mathrm {d} y\end{aligned}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/c8be5b7d065826eaeaeb6d191a36df3a52b340cc)




