対移動平均比率法

対移動平均比率法（たいいどうへいきんひりつほう、英: ratio-to-moving-average method）は，過去の時系列データから，将来の数値を予測する方法の一つ。需要予測などに用いる。季節変動や曜日変動などの周期性がある場合に有効である。移動平均法の一種であり、比較的単純な方法であるが、実用的な結果を出すことが多い。竹安数博らが1997年に発表した^[1]。

原理

まず、過去のデータから各季節ごとの季節指数を求める。次に、傾向を延長し、それに季節指数を掛けて予測値を得る。

需要などの変動は、傾向変動、循環変動、季節変動、不規則変動などに分解される。

→「季節調整」も参照

対移動平均比率法では、時系列データ A を傾向変動 (F) と季節変動 (E) の積として捉える。1周期分（例えば1年分）のデータの平均値は、季節変動を除去した値になる。平均値を取る範囲をずらしていくと滑らかな系列（移動平均）B が得られる。そして、原データ A の平均値 B に対する比（対移動平均比率）C を季節ごとに平均した値（季節別平均値）D を正規化して、季節ごとの係数である季節指数 E を知る。

元の時系列データ A を季節指数 E で割れば、季節変動を取り除いた滑らかな系列 F が得られる（F には循環変動と不規則変動だけが残っている）。これを回帰分析して、傾向変動（トレンド）とする（傾向推定）。将来を予測するときは、まず回帰式によって傾向値 F を延長して将来の傾向値 f を推測（外挿）し、次に各季節の季節指数 E を掛けて予測値を得る。

「季節変動」は、必ずしも1年を周期とする季節に限らず、1週を周期とする曜日（曜日変動）でもよい。（竹安ら^[2]は、これらを総括して「期間変動」と呼んでいる。そのとき、季節指数を「期間指数」と呼ぶ。）循環の周期が一定している変動ならば、この方法が適用できる。

手法

ここでは、1年を周期とする「季節変動」をもつ春・夏・秋・冬ごとの季節データを想定して、手法の用語を記述する。過去の数周期分のデータがあるとする。

1. 周期性をもつ時系列の原データ A から、1周期分の移動平均の系列 B を計算する。
2. 各季節データ A の移動平均 B に対する比率（対移動平均比率）C を計算する。
3. 各季節ごとに対移動平均比率 C の平均値（季節別平均値）D を計算する。
4. 季節別平均値 D を D 全体の平均値で割って、各季節の季節指数 E を得る。^[3]
5. 原データ A を季節指数 E で割り、滑らかな傾向値 F を得る。
6. 過去の傾向値 F を（最小二乗法によって）回帰分析する。
7. 将来の傾向値 f を（回帰式によって）推測する。
8. 将来の推測値 f に季節ごとの季節指数 E を掛けた予測値を計算する。

実は、1周期内のデータ数（春・夏・秋・冬の場合は 4）が偶数の場合は移動平均の計算に少し工夫が必要であり、その手法は下の 3.2（#周期が偶数である場合）に示す。

数値例

まず、1周期内のデータ数が奇数である場合の数値例によって、手法の主要部分の実際を示す。

周期が奇数である場合

過去3週間分の日々のデータから、次の1週間分を予測している。

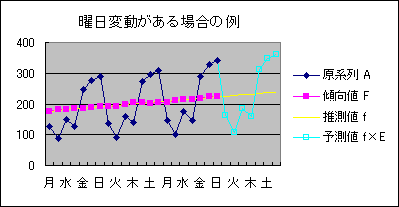
1週を周期とする曜日変動のある場合の計算例とそのグラフを示す。過去の3周期分（先々週から今週まで）の日ごとのデータから、来週1週間分を予測する。

表の下にある段階 6. 傾向の推定 では、傾向値を推定する何らかの手法を用いる。ここでは、直線による回帰分析をしている。

曜日による変動がある場合の例

段階	週	月	火	水	木	金	土	日	平均
0. 原系列 A	先々週	126	87	149	127	246	276	288
	先週	138	91	160	139	274	297	309
	今週	147	101	174	147	289	328	341
1. 移動平均 B	先々週	--	--	--	185.6	187.3	187.9	189.4
	先週	191.1	195.1	198.1	201.1	202.4	203.9	205.9
	今週	207.0	209.1	213.6	218.1	--	--	--
2. 対移動平均 　比率 　　C = A/B	先々週	--	--	--	0.684	1.313	1.469	1.521
	先週	0.722	0.466	0.808	0.691	1.354	1.457	1.501
	今週	0.710	0.483	0.815	0.674	--	--	--
3. 曜日別平均値	D	0.716	0.475	0.811	0.683	1.334	1.463	1.511	0.999
4. 曜日指数	E	0.717	0.475	0.812	0.684	1.335	1.464	1.512	1.000
5. 傾向値 　　F = A/E	先々週	175.8	183.1	183.5	185.7	184.3	188.5	190.5
	先週	192.5	191.5	197.1	203.3	205.3	202.8	204.3
	今週	205.1	212.5	214.3	215.0	216.5	224.0	225.5
7. 推測値 f	来週	225.2	227.5	229.8	232.0	234.3	236.6	238.9
8. 予測値 f ×E	来週	161.4	108.1	186.5	158.7	312.8	346.4	361.2

6. 傾向の推定 - 傾向値の系列 F_x から最小二乗法によって回帰直線 f = ax + b の係数を求めると、a = 2.29, b = 177.2 を得る。ここで、x はデータの番号とする (x = 0, 1, 2, ..., 20)。

7. 推測値 - 回帰直線 f = 2.29x + 177.2 を用いて、来週の傾向値データ f_x を推測する (x = 21, 22, ..., 27)。

周期が偶数である場合

1周期内のデータ数が偶数である場合には、1. 移動平均 B を計算するときに少し工夫が要る。例えば、単純移動平均をさらに二つずつ平均する方法がある^[1]。こうすると移動平均の項数が1つ少なくなるが、各季節の前後のデータを対称かつ均等に扱った平均値が得られる。

周期内のデータ数が偶数である場合の移動平均

段階	前々年								前年								今年
季節	春		夏		秋		冬		春'		夏'		秋'		冬'		春"		夏"		秋"		冬"
0. 原系列 A	126		87		246		288		138		91		274		309		147		101		289		341
4項の単純 　移動平均		--		186.8		189.8		190.8		197.8		203.0		205.3		207.8		211.5		219.5		--
1. 2項ずつの 　移動平均 B	--		--		188.3		190.3		194.3		200.4		204.1		206.5		209.6		215.5		--		--

例えば、表の左下隅の値 188.3 は、前々年の春と前年の春'を平均した値と、夏，秋，冬の値との平均になっている。

188.3 ＝ { 186.8 ＋ 189.8 } / 2
      ＝ { (春＋夏＋秋＋冬)/4 ＋ (夏＋秋＋冬＋春')/4 } / 2
      ＝ {  春    ＋  2×(夏＋秋＋冬)  ＋     春'}/4  / 2
      ＝ {  春/2  ＋      夏＋秋＋冬   ＋   春'/2}/4  …… 秋を中心として対称
      ＝ { (春＋春')/2 ＋夏＋秋＋冬 }/4

歴史

対移動平均比率法は、竹安数博が開発し、1997年に『新しい経営数学』^[1]で発表した。

竹安らは、2006年にこの手法に関しての特許を取得している^[2]。