指数分布

指数分布（しすうぶんぷ、英: exponential distribution）とは、確率論および統計学における連続確率分布の一種である。これは例えばポアソン過程——事象が連続して独立に一定の発生率で起こる過程——に従う事象の時間間隔を記述する。

指数分布

確率密度関数
累積分布関数
母数	${\displaystyle \lambda (=1/\theta )>0}$
台	${\displaystyle [0,\infty )}$
確率密度関数	${\displaystyle \lambda e^{-\lambda x}}$
累積分布関数	${\displaystyle 1-e^{-\lambda x}}$
期待値	${\displaystyle 1/\lambda }$
中央値	${\displaystyle (\ln 2)/\lambda }$
最頻値	${\displaystyle 0}$
分散	${\displaystyle 1/\lambda ^{2}}$
歪度	${\displaystyle 2}$
超過尖度	${\displaystyle 6}$
エントロピー	${\displaystyle 1-\ln \lambda }$
モーメント母関数	${\displaystyle (1-t/\lambda )^{-1}{\text{ for }}t<\lambda }$
特性関数	${\displaystyle (1-i\,t/\lambda )^{-1}}$
フィッシャー情報量	${\displaystyle 1/\lambda ^{2}}$

定義

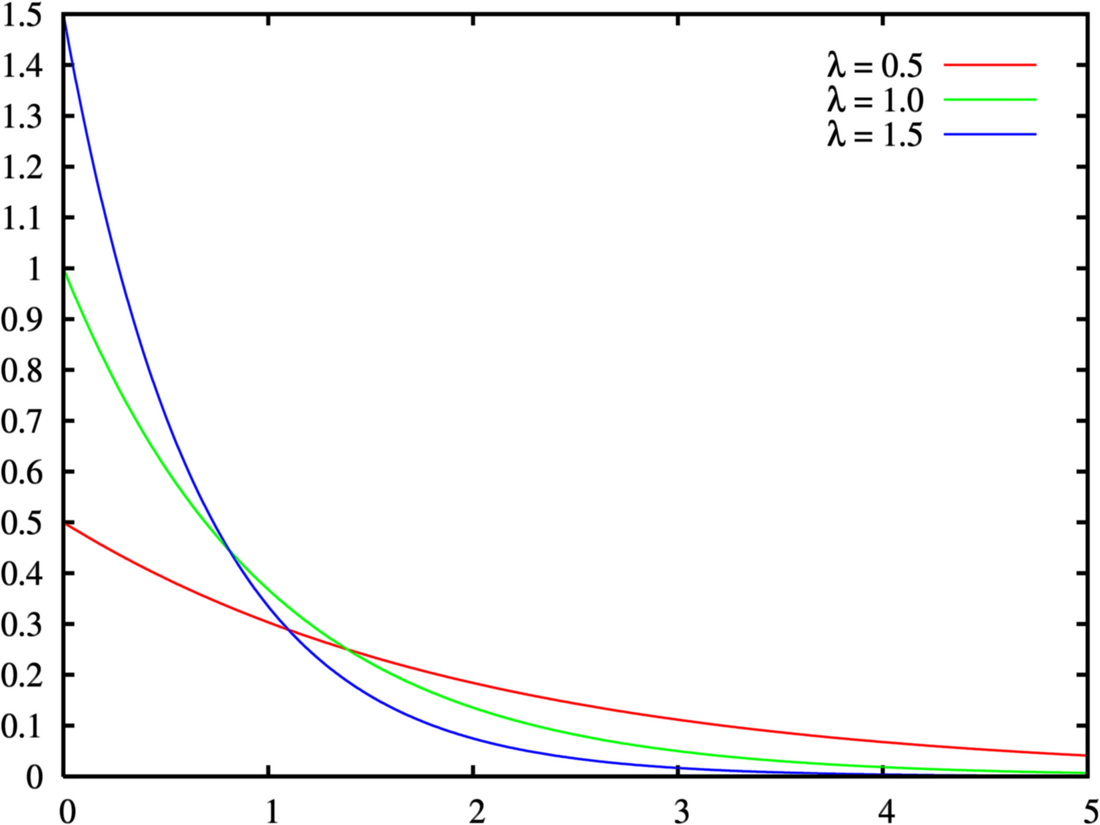
指数分布は台 (0, ∞) を持ち、母数 λ > 0 に対して確率密度関数が

${\displaystyle f(x;\lambda )=\lambda e^{-\lambda x}}$

で与えられる^[1]。このとき、累積分布関数は

${\displaystyle F(x;\lambda )=1-e^{-\lambda x}}$

となる^[2]。

尺度母数 θ = 1/λ を用いると、確率密度関数の等価な定義は

${\displaystyle f(x;\theta )={\frac {1}{\theta }}f(x/\theta ;1)={\frac {1}{\theta }}e^{-x/\theta }}$

として与えられる。

性質

期待値・分散

定義より、期待値 E(x) および分散 V(x) はそれぞれ以下のようになる^[3]。

${\displaystyle E(x)={\frac {1}{\lambda }}=\theta ,\ \ \ V(x)={\frac {1}{\lambda ^{2}}}=\theta ^{2}}$

他の分布との関係

形状母数（英語版）が 1 であるガンマ分布は指数分布である。

独立で同一の指数分布に従う確率変数の和はアーラン分布に従う。アーラン分布の形状母数を 1 とすると指数分布に自明に一致する。

また、自由度2のカイ二乗分布は θ = 2 の指数分布と一致する。ワイブル分布における係数 m = 1 とおいた特殊な場合でもある。

無記憶性

指数分布は、幾何分布と同様に無記憶性 (memoryless) と呼ばれる性質を持つ。これは、確率変数 X が

${\displaystyle \forall s,t>0,\ \ P(X>s+t\mid X>s)=P(X>t)}$

なる等式を満たすことをいう。すなわち、時刻 s までに事象が生起しなかったという情報が与えられたとき、その事象がさらに t 時間の間生起しない条件付き確率は、（時刻 s まで事象が生起しなかったという情報が完全に忘れ去られ、改めてその時点から観測を始めて）t 時間の間事象が生起しない確率に一致するという意味である。

上述した累積分布関数の定義より、指数分布に従う確率変数がこの性質を満たすことは容易に示される^[4]。逆に、この性質を満たす連続確率分布が指数分布のみであることも証明されている^[5]。

パラメータ推定

この節では、確率変数 X が未知なるパラメータλの指数分布に従うとし、${\displaystyle \{x\}=x_{1},\ldots ,x_{n}}$が X のn個の独立なサンプルであるとする。また、

${\displaystyle {\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}}$

とする。今、パラメータλを${\displaystyle x_{1},\ldots ,x_{n}}$を用いて推定することを考える。

最尤推定

λの最尤推定は、以下の尤度を最大化するλとして与えられる:

${\displaystyle L(\{x\}|\lambda )=\prod _{i=1}^{n}\lambda \exp(-\lambda x_{i})=\lambda ^{n}\exp(-n\lambda {\bar {x}})}$

したがって、λの最尤推定として

${\displaystyle {\hat {\lambda }}_{\mathrm {mle} }={\frac {1}{\bar {x}}}}$

が得られる。ただし、これは不偏推定量ではない。実際、${\displaystyle {\hat {\lambda }}_{\mathrm {mle} }}$の期待値は${\displaystyle n>1}$の場合に

${\displaystyle \operatorname {E} \left[{\hat {\lambda }}_{\mathrm {mle} }\right]={\frac {n}{n-1}}\lambda }$

と計算され、${\displaystyle \lambda }$に一致しない。一方、${\displaystyle {\bar {x}}}$は${\displaystyle \theta }$の最尤推定量^[6]かつ不偏推定量^[7] である。

フィッシャー情報量

フィッシャー情報量は

${\displaystyle {\mathcal {I}}(\lambda )=\left\langle \left({\frac {\partial }{\partial \lambda }}\ln \left(f(x;\lambda )\right)\right)^{2}\right\rangle ={\frac {1}{\lambda ^{2}}}}$

と計算される。

共役分布を用いたベイズ推定

${\displaystyle X}$が指数分布に従うモデルで${\displaystyle \lambda }$を推定する場合、${\displaystyle \lambda }$の事前分布としてガンマ分布を利用すると、これは共役事前分布（英語版）となる。すなわち、${\displaystyle \lambda }$の事後分布もガンマ分布となる。

実際、事前分布を

${\displaystyle p(\lambda )=\operatorname {Gamma} (\lambda$ ;\alpha ,\beta )={\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}\lambda ^{\alpha -1}\exp(-\beta \lambda )}

としておくと、事後分布は

${\displaystyle p(\lambda |\{x\})\propto p(\lambda )L(\{x\}|\lambda )\propto \left(\lambda ^{\alpha -1}\exp(-\beta \lambda )\right)\left(\lambda ^{n}\exp(-n\lambda {\bar {x}})\right)}$

を満たすため、

${\displaystyle p(\lambda |\{x\})=\operatorname {Gamma} (\lambda$ ;\alpha +n,\beta +n{\bar {x}})}

がわかる。この場合、ハイパーパラメータはそれぞれ${\displaystyle \alpha }$が事前の観測数、${\displaystyle \beta }$が事前の観測値の和として解釈される。

生成

逆関数法を用いて指数分布に従う確率変数を生成することができる。一様乱数 ${\displaystyle U(0,1)}$で、${\displaystyle x\sim \mathrm {Exp} (\lambda )}$ は以下の式で得られる:

${\displaystyle x=-{\frac {1}{\lambda }}\ln U}$