線型代数学の基本定理

数学の分野における線型代数学の基本定理（せんけいだいすうがくのきほんていり、英: fundamental theorem of linear algebra）とは、ベクトル空間に関するいくつかの定理である。それらの定理においては、ある m×n 行列 A の階数 r や、その特異値分解

${\displaystyle A=U\Sigma V^{T}\ }$

に関する内容が、具体的にまとめられている。はじめに、各行列 ${\displaystyle A\in \mathbf {R} ^{m\times n}}$（行列 ${\displaystyle A}$ は ${\displaystyle m}$ 個の行と ${\displaystyle n}$ 個の列を持つ）は、「四つの基本部分空間」を導く。それらを次の表に示す：

部分空間の名前	定義	含まれる空間	次元	基底
列空間、値域あるいは像	${\displaystyle \mathrm {im} (A)}$ あるいは ${\displaystyle \mathrm {range} (A)}$	${\displaystyle \mathbf {R} ^{m}}$	${\displaystyle r}$（階数）	${\displaystyle U}$ の初めの ${\displaystyle r}$ 列
零空間あるいは核	${\displaystyle \mathrm {ker} (A)}$ あるいは ${\displaystyle \mathrm {null} (A)}$	${\displaystyle \mathbf {R} ^{n}}$	${\displaystyle n-r}$（退化次数）	${\displaystyle V}$ の最後の ${\displaystyle (n-r)}$ 列
行空間あるいは余像	${\displaystyle \mathrm {im} (A^{T})}$ あるいは ${\displaystyle \mathrm {range} (A^{T})}$	${\displaystyle \mathbf {R} ^{n}}$	${\displaystyle r}$（階数）	${\displaystyle V}$ の初めの ${\displaystyle r}$ 列
左零空間あるいは余核	${\displaystyle \mathrm {ker} (A^{T})}$ あるいは ${\displaystyle \mathrm {null} (A^{T})}$	${\displaystyle \mathbf {R} ^{m}}$	${\displaystyle m-r}$（余階数）	${\displaystyle U}$ の最後の ${\displaystyle (m-r)}$ 列

続いて、次が成立する：

1. ${\displaystyle \mathbf {R} ^{n}}$ において、${\displaystyle \mathrm {ker} (A)=(\mathrm {im} (A^{T}))^{\perp }}$ である。すなわち零空間は、行空間の直交補空間である。
2. ${\displaystyle \mathbf {R} ^{m}}$ において、${\displaystyle \mathrm {ker} (A^{T})=(\mathrm {im} (A))^{\perp }}$ である。すなわち左零空間は、列空間の直交補空間である。

行列 A に関する四つの部分空間

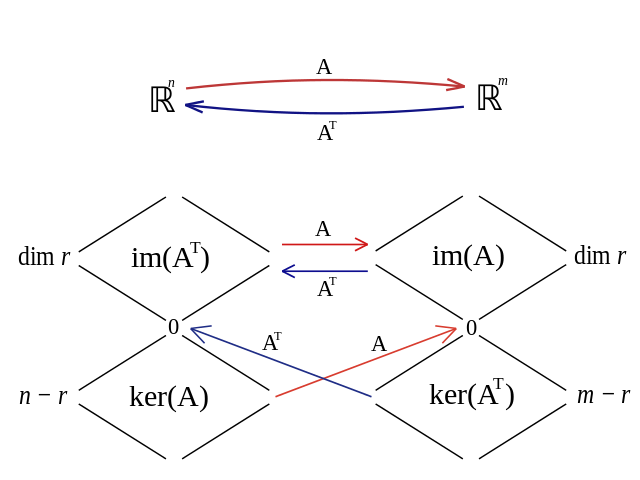
各部分空間の次元は階数・退化次数の定理によって関連付けられており、上表の定理に従う。

また、これら全ての空間は、基底の選び方に依らず、本質的に定義される。そのような場合この定理は、抽象的ベクトル空間や作用素および双対空間として、${\displaystyle A\colon V\to W}$ および ${\displaystyle A^{*}\colon W^{*}\to V^{*}}$ を用いて次のように言い直すことが出来る：${\displaystyle A^{*}}$ の核および像は、${\displaystyle A}$ の余核および余像に、それぞれ等しい。

関連項目

• 階数・退化次数の定理
• 閉値域の定理

参考文献

• Strang, Gilbert. Linear Algebra and Its Applications. 3rd ed. Orlando: Saunders, 1988.
• Strang, Gilbert (1993), “The fundamental theorem of linear algebra”, American Mathematical Monthly 100 (9): 848–855, doi:10.2307/2324660, JSTOR 2324660, http://www.eng.iastate.edu/~julied/classes/CE570/Notes/strangpaper.pdf

外部リンク

• Gilbert Strang, MIT Linear Algebra Lecture on the Four Fundamental Subspaces at Google Video, from MIT OpenCourseWare