구간의 분할

수학에서, 실직선 위의 구간 [a, b]의 분할(分割, 영어: partition)이란 다음의

a = x₀ < x₁ < x₂ < ... < x_n = b

관계에 있는 실수 x₀, x₁, x₂, ..., x_n로 구성된 유한 수열이다.

리만 합에서 사용하는 구간의 태그된 분할. 분할 자체는 아래의 회색 선으로 표시하였고, 그 중 한 부분구간을 빨간색으로 나타내었다.

다르게 말하면, 콤팩트 구간 I의 분할이란 I의 시작점에서 끝점까지 순증가하는 수들로 구성된 수열이다. 각 구간 [x_i, x_{i + 1}]을 분할의 부분구간이라 한다.

분할의 세분

구간 [a,b]의 분할 P와 Q에 대해, Q가 P의 모든 점을 포함할 때 Q를 P의 세분(영어: refinement)이라 하고 Q가 P보다 섬세하다고 한다. 또 두 분할 P와Q에 대하여 두 분할의 모든 점들로 구성된 분할을 공통세분이라 하고 P ∨ Q라 쓴다.^[1] 어떤 분할이 다른 분할의 세분일 때, 더 섬세한 분할이 더 크다고 순서 관계를 정의하면 이는 부분 순서가 된다.

분할의 노름

아래처럼 주어진 분할

x₀ < x₁ < x₂ < ... < x_n

의 노름(영어: norm) 또는 메시(영어: mesh)란 각 부분구간들의 길이의 최댓값

max{|x_i − x_i−1| : i = 1, ... , n }

이다.^[2][3]

태그된 분할

주어진 구간에 대해 태그된 분할(영어: tagged partition)이란^[4] 각 i에 대해 다음 조건

x_i ≤ t_i ≤ x_{i + 1}

을 만족하는 수들로 구성된 유한 수열 t₀, ..., t_{n − 1}을 가지는 분할이다. 다시 말해 태그된 분할이란 각 부분구간들에서 점을 한 개씩 선택한 분할로, 기존 분할과 동일하게 노름을 정의한다. 태그된 분할 P와 Q에 대해 Q가 P의 분할 위의 모든 점들과 함께 모든 태그들, 즉 각 부분구간에서 선택한 점들을 모두 포함할 때 Q가 P의 세분이라 한다.

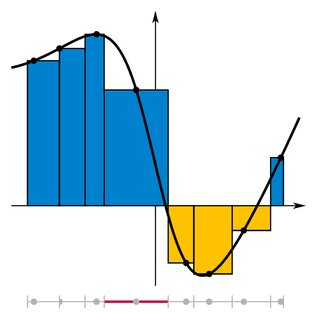
리만 합

구간의 분할은 리만 적분과 리만-스틸체스 적분에서 사용된다. 주어진 구간의 분할이 더 섬세할수록 분할의 노름은 0에 가까워지고, 따라서 리만 합은 리만 적분값에 수렴한다.^[5]

같이 보기

• 리만 합
• 리만 적분
• 집합의 분할