구간연산

구간 연산 또는 구간 산술(區間算術, 영어: interval arithmetic, 다른 이름: 구간 수학, 구간 해석 또는 구간 계산)은 함수 경계를 계산하여 수학적 계산에서 반올림 및 측정 오차를 완화하는 데 사용되는 수학적 기술이다. 수치해석에서 수치계산의 결과 범위를 예측하는 데 쓰는 연산이다. 구간 산술이 포함된 수치 방법은 상대적으로 신뢰할 수 있고 수학적으로 올바른 결과를 보장할 수 있다. 단일 숫자로 값을 표현하는 대신, 구간 연산 또는 구간 수학은 각 값을 가능성 범위로 나타낸다.

오차 함수 (청록색) 및 구간 값 근사 (빨간색)

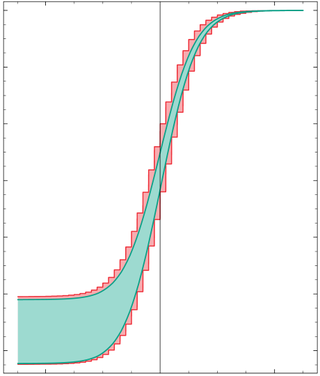
수학적으로 불확실한 실수 값 변수 ${\displaystyle x}$를 다루는 대신, 구간 연산은 ${\displaystyle x}$가 가질 수 있는 값의 범위를 정의하는 구간 ${\displaystyle [a,b]}$를 다룬다. 즉, 변수 ${\displaystyle x}$의 어떤 값도 ${\displaystyle a}$와 ${\displaystyle b}$ 사이의 닫힌 구간에 놓여 있다. 함수 ${\displaystyle f}$는 ${\displaystyle x}$에 적용될 때 ${\displaystyle [c,d]}$ 구간을 생성하며, 이 구간은 모든 ${\displaystyle x\in [a,b]}$에 대한 ${\displaystyle f(x)}$의 모든 가능한 값을 포함한다.

구간 연산은 다양한 목적에 적합하다. 가장 일반적인 사용은 과학 분야, 특히 계산이 소프트웨어에 의해 처리될 때 계산의 반올림 오차와 물리적 및 기술적 매개변수의 정확한 값에 대한 불확실성을 추적하는 데 사용된다. 후자는 종종 측정 오차 및 구성 요소의 공차 또는 계산 정확도 한계로 인해 발생한다. 구간 연산은 또한 방정식(예: 미분방정식) 및 최적화 문제에 대한 보장된 해를 찾는 데 도움이 된다.

a₁ < a₂인 실수에 대해서 [a₁, a₂] = { x | ${\displaystyle a_{1}\leq x\leq a_{2}}$}라고 하자. A = [a₁, a₂], B = [b₁, b₂]라 하면

A + B = [a₁ + b₁, a₂ + b₂]

A - B = [a₁ - b₂, a₂ - b₁]

A · B = [min(a₁b₁, a₂b₁, a₁b₂, a₂b₂), max(a₁b₁, a₂b₁, a₁b₂, a₂b₂)]

A ÷ B = [a₁, a₂] · ${\displaystyle \left[{\frac {1}{b_{2}}},{\frac {1}{b_{1}}}\right]}$ = ${\displaystyle \left[min\left({\frac {a_{1}}{b_{2}}},{\frac {a_{1}}{b_{1}}},{\frac {a_{2}}{b_{2}}},{\frac {a_{2}}{b_{1}}}\right),max\left({\frac {a_{1}}{b_{2}}},{\frac {a_{1}}{b_{1}}},{\frac {a_{2}}{b_{2}}},{\frac {a_{2}}{b_{1}}}\right)\right]}$

서론

구간 산술의 주요 목적은 하나 이상의 변수에서 함수의 범위에 대한 상한과 하한을 계산하는 간단한 방법을 제공하는 것이다. 이러한 끝점은 반드시 범위의 실제 상한 또는 하한일 필요는 없다. 이러한 값을 정확하게 계산하는 것은 어렵거나 불가능할 수 있기 때문이다. 경계는 단지 함수의 범위를 부분집합으로 포함하기만 하면 된다.

이러한 처리는 일반적으로 실수 구간에 국한되므로, 다음과 같은 형태의 양은 허용된다.

${\displaystyle [a,b]=\{x\in \mathbb {R} \mid a\leq x\leq b\},}$

여기서 ${\displaystyle a={-\infty }}$ 및 ${\displaystyle b={\infty }}$가 허용된다. ${\displaystyle a}$ 또는 ${\displaystyle b}$ 중 하나가 무한대이면 구간은 무한 구간이 되고, 둘 다 무한대이면 구간은 확장된 실직선이 된다. 실수 ${\displaystyle r}$은 구간 ${\displaystyle [r,r]}$로 해석될 수 있으므로 구간과 실수는 자유롭게 결합될 수 있다.

예시

키 1.80m의 사람의 체중 m(킬로그램)에 대한 체질량 지수

한 사람의 체질량 지수(BMI) 계산을 고려해 보자. BMI는 사람의 체중(킬로그램)을 키(미터)의 제곱으로 나눈 값이다. 어떤 사람이 1킬로그램 단위의 정밀도를 가진 저울을 사용하는데, 중간 값은 구별할 수 없고 실제 체중은 가장 가까운 정수로 반올림된다고 가정해 보자. 예를 들어, 저울은 가장 가까운 킬로그램 단위로만 값을 표시할 수 있으므로 79.6kg과 80.3kg은 구별할 수 없다. 저울이 80kg을 읽을 때, 그 사람이 정확히 80.0kg일 가능성은 낮다. 따라서 저울이 80kg을 표시한다는 것은 79.5kg에서 80.5kg 사이의 체중, 즉 구간 ${\displaystyle [79.5,80.5)}$를 나타낸다.

80kg이고 키가 1.80m인 남성의 BMI는 약 24.7이다. 79.5kg에 동일한 키를 적용하면 BMI는 24.537이 되고, 80.5kg에 적용하면 24.846이 된다. 체질량은 연속적이고 지정된 체중 구간 내의 모든 값에 대해 항상 증가하므로 실제 BMI는 ${\displaystyle [24.537,24.846]}$ 구간 내에 있어야 한다. 전체 구간이 정상 체중과 과체중 사이의 경계인 25보다 작으므로, 이 남성은 정상 체중이라고 확신할 수 있다.

이 예시의 오차는 결론(정상 체중)에 영향을 미치지 않지만, 이것이 일반적으로 참은 아니다. 만약 남자가 약간 더 무거웠다면, BMI의 범위는 경계 값인 25를 포함할 수 있다. 그러한 경우, 저울의 정밀도는 확정적인 결론을 내리기에 불충분할 것이다.

BMI 예시의 범위는 계산된 구간의 상위 집합이므로 ${\displaystyle [24.5,24.9]}$로 보고될 수 있다. 그러나 이 구간은 가능한 BMI 값을 포함하지 않으므로 ${\displaystyle [24.6,24.8]}$로는 보고될 수 없다.

여러 구간

키 L(미터)에 따른 다양한 체중의 체질량 지수

키와 체중 모두 BMI 값에 영향을 미친다. 위 예시에서는 체중 변화만을 고려했지만, 키 또한 불확실성의 대상이다. 미터 단위의 키 측정값은 일반적으로 가장 가까운 센티미터로 반올림된다. 1.79미터로 기록된 측정값은 ${\displaystyle [1.785,1.795)}$ 구간의 키를 나타낸다. BMI는 체중에 대해 균일하게 증가하고 키에 대해 감소하므로, 각 구간의 최저값과 최고값을 대입한 다음 가장 낮은 결과와 가장 높은 결과를 경계로 선택하여 오차 구간을 계산할 수 있다. 따라서 BMI는 다음 구간에 존재해야 한다.

${\displaystyle {\frac {[79.5,80.5)}{[1.785,1.795)^{2}}}\subseteq [24.673,25.266].}$

이 경우, 남자는 정상 체중일 수도 있고 과체중일 수도 있다. 체중 및 키 측정값이 결정적인 결론을 내리기에 충분히 정확하지 않았다.

구간 연산자

두 구간에 대한 이항 연산 ${\displaystyle \star }$는 덧셈 또는 곱셈과 같이 다음과 같이 정의된다.

${\displaystyle [x_{1},x_{2}]{\,\star \,}[y_{1},y_{2}]=\{x\star y\,|\,x\in [x_{1},x_{2}]\,\land \,y\in [y_{1},y_{2}]\}.}$

즉, ${\displaystyle x}$와 ${\displaystyle y}$가 각각의 구간에 있을 때 ${\displaystyle x\star y}$의 모든 가능한 값들의 집합이다. 만약 ${\displaystyle \star }$가 구간의 각 피연산자에 대해 단조적이라면 (분모가 ${\displaystyle 0}$을 포함하는 나눗셈을 제외한 네 가지 기본 산술 연산의 경우에 해당), 극값은 피연산자 구간의 끝점에서 발생한다. 모든 조합을 나열하면, 이를 다음과 같이 표현할 수 있다.

${\displaystyle [x_{1},x_{2}]\star [y_{1},y_{2}]=\left[\min\{x_{1}\star y_{1},x_{1}\star y_{2},x_{2}\star y_{1},x_{2}\star y_{2}\},\max\{x_{1}\star y_{1},x_{1}\star y_{2},x_{2}\star y_{1},x_{2}\star y_{2}\}\right],}$

단, ${\displaystyle x\in [x_{1},x_{2}]}$ 및 ${\displaystyle y\in [y_{1},y_{2}]}$의 모든 ${\displaystyle x,y}$에 대해 ${\displaystyle x\star y}$가 정의되어야 한다.

실용적인 응용을 위해, 이것은 더 단순화될 수 있다.

• 덧셈: $${\displaystyle [x_{1},x_{2}]+[y_{1},y_{2}]=[x_{1}+y_{1},x_{2}+y_{2}]}$$
• 뺄셈: $${\displaystyle [x_{1},x_{2}]-[y_{1},y_{2}]=[x_{1}-y_{2},x_{2}-y_{1}]}$$
• 곱셈: $${\displaystyle [x_{1},x_{2}]\cdot [y_{1},y_{2}]=[\min\{x_{1}y_{1},x_{1}y_{2},x_{2}y_{1},x_{2}y_{2}\},\max\{x_{1}y_{1},x_{1}y_{2},x_{2}y_{1},x_{2}y_{2}\}]}$$
• 나눗셈: $${\displaystyle {\frac {[x_{1},x_{2}]}{[y_{1},y_{2}]}}=[x_{1},x_{2}]\cdot {\frac {1}{[y_{1},y_{2}]}},}$$ 여기서 $${\displaystyle {\begin{aligned}{\frac {1}{[y_{1},y_{2}]}}&=\left[{\tfrac {1}{y_{2}}},{\tfrac {1}{y_{1}}}\right]&&{\textrm {if}}\;0\notin [y_{1},y_{2}]\\{\frac {1}{[y_{1},0]}}&=\left[-\infty ,{\tfrac {1}{y_{1}}}\right]\\{\frac {1}{[0,y_{2}]}}&=\left[{\tfrac {1}{y_{2}}},\infty \right]\\{\frac {1}{[y_{1},y_{2}]}}&=\left[-\infty ,{\tfrac {1}{y_{1}}}\right]\cup \left[{\tfrac {1}{y_{2}}},\infty \right]\subseteq [-\infty ,\infty ]&&{\textrm {if}}\;0\in (y_{1},y_{2})\end{aligned}}}$$

마지막 경우는 ${\displaystyle (1/y_{1},1/y_{2})}$의 제외에 대한 유용한 정보를 잃게 된다. 따라서 ${\displaystyle \left[-\infty ,{\tfrac {1}{y_{1}}}\right]}$와 ${\displaystyle \left[{\tfrac {1}{y_{2}}},\infty \right]}$를 별도의 구간으로 작업하는 것이 일반적이다. 더 일반적으로, 불연속 함수로 작업할 때 ${\textstyle \bigcup _{i}\left[a_{i},b_{i}\right]}$ 형태의 소위 다중 구간을 사용하여 계산하는 것이 유용할 때가 있다. 해당 다중 구간 연산은 (일반적으로 서로소인) 구간 집합을 유지하며, 겹치는 구간을 통합하는 기능도 제공한다.^[1]

양수 구간의 곱셈

구간 곱셈은 종종 두 번의 곱셈만 필요하다. ${\displaystyle x_{1}}$, ${\displaystyle y_{1}}$이 음수가 아니면,

${\displaystyle [x_{1},x_{2}]\cdot [y_{1},y_{2}]=[x_{1}\cdot y_{1},x_{2}\cdot y_{2}],\qquad {\text{ if }}x_{1},y_{1}\geq 0.}$

곱셈은 가장자리가 변하는 사각형의 넓이로 해석할 수 있다. 결과 구간은 가장 작은 값부터 가장 큰 값까지 모든 가능한 넓이를 포함한다.

이러한 정의의 도움으로 ${\displaystyle f(a,b,x)=a\cdot x+b.}$와 같은 간단한 함수의 범위를 이미 계산할 수 있다. 예를 들어, ${\displaystyle a=[1,2]}$, ${\displaystyle b=[5,7]}$, ${\displaystyle x=[2,3]}$일 경우:

${\displaystyle f(a,b,x)=([1,2]\cdot [2,3])+[5,7]=[1\cdot 2,2\cdot 3]+[5,7]=[7,13].}$

표기법

구간의 표기법을 줄이기 위해 괄호를 사용할 수 있다.

${\displaystyle [x]\equiv [x_{1},x_{2}]}$는 구간을 나타내는 데 사용될 수 있다. 이러한 간결한 표기법에서 ${\displaystyle [x]}$를 단일 지점 구간 ${\displaystyle [x_{1},x_{1}]}$과 일반적인 구간 사이에서 혼동해서는 안 된다. 모든 구간의 집합에 대해서는

${\displaystyle [\mathbb {R} ]:=\left\{\,[x_{1},x_{2}]\,|\,x_{1}\leq x_{2}{\text{ and }}x_{1},x_{2}\in \mathbb {R} \cup \{-\infty ,\infty \}\right\}}$

를 약어로 사용할 수 있다. 구간 벡터 ${\displaystyle \left([x]_{1},\ldots ,[x]_{n}\right)\in [\mathbb {R} ]^{n}}$에 대해서는 굵은 글꼴을 사용할 수 있다. ${\displaystyle [\mathbf {x} ]}$.

초등 함수

단조함수의 값 도메인

네 가지 기본 연산자 외에 구간 함수도 정의할 수 있다.

하나의 변수에 대한 단조함수의 경우, 값의 범위는 계산하기 쉽다. 구간 ${\displaystyle [x_{1},x_{2}]}$에서 ${\displaystyle f:\mathbb {R} \to \mathbb {R} }$이 단조 증가(또는 감소)한다면, ${\displaystyle y_{1}<y_{2}}$를 만족하는 모든 ${\displaystyle y_{1},y_{2}\in [x_{1},x_{2}]}$에 대해 ${\displaystyle f(y_{1})\leq f(y_{2})}$ (또는 ${\displaystyle f(y_{2})\leq f(y_{1})}$)이다.

따라서 구간 ${\displaystyle [y_{1},y_{2}]\subseteq [x_{1},x_{2}]}$에 해당하는 범위는 함수를 그 끝점에 적용하여 계산할 수 있다.

${\displaystyle f([y_{1},y_{2}])=\left[\min \left\{f(y_{1}),f(y_{2})\right\},\max \left\{f(y_{1}),f(y_{2})\right\}\right].}$

이로부터 구간 함수에 대한 다음과 같은 기본 특징들을 쉽게 정의할 수 있다.

• 지수 함수: ${\displaystyle a^{[x_{1},x_{2}]}=[a^{x_{1}},a^{x_{2}}]}$ (${\displaystyle a>1}$인 경우),
• 로그: 양수 구간 ${\displaystyle [x_{1},x_{2}]}$ 및 ${\displaystyle a>1}$인 경우 ${\displaystyle \log _{a}[x_{1},x_{2}]=[\log _{a}{x_{1}},\log _{a}{x_{2}}]}$,
• 홀수 거듭제곱: 홀수 ${\displaystyle n\in \mathbb {N} }$인 경우 ${\displaystyle [x_{1},x_{2}]^{n}=[x_{1}^{n},x_{2}^{n}]}$.

짝수 제곱의 경우, 고려되는 값의 범위가 중요하며 곱셈을 수행하기 전에 처리되어야 한다. 예를 들어, ${\displaystyle x\in [-1,1]}$에 대한 ${\displaystyle x^{n}}$은 ${\displaystyle n=2,4,6,\ldots }$일 때 ${\displaystyle [0,1]}$ 구간을 생성해야 한다. 그러나 ${\displaystyle [-1,1]^{n}}$이 ${\displaystyle [-1,1]\cdot [-1,1]\cdot \cdots \cdot [-1,1]}$ 형태의 반복되는 구간 곱셈으로 계산되면, 결과는 ${\displaystyle [-1,1]}$이 되며, 이는 필요 이상으로 넓다.

더 일반적으로, 구간별 단조 함수에 대해서는 구간의 끝점 ${\displaystyle x_{1},x_{2}}$와 함수 단조성이 방향을 바꾸는 점인 소위 구간 내의 임계점을 고려하는 것으로 충분하다고 말할 수 있다. 사인 및 코사인 함수의 경우, 임계점은 각각 ${\displaystyle n\in \mathbb {Z} }$에 대해 ${\displaystyle \left({\tfrac {1}{2}}+n\right)\pi }$ 또는 ${\displaystyle n\pi }$이다. 따라서 결과 구간이 최소 두 개의 극값을 포함하는 경우, 구간 내에서 최대 5개의 점만 고려하면 된다. 사인 및 코사인의 경우, 임계점은 쉽게 미리 계산된 값인 -1, 0, 1로 이어지므로 끝점만 완전히 평가하면 된다.

일반 함수의 구간 확장

일반적으로 많은 함수에 대해 출력 구간의 그러한 간단한 설명을 찾는 것은 쉽지 않을 수 있다. 그러나 함수를 구간 연산로 확장하는 것은 여전히 가능할 수 있다. ${\displaystyle f:\mathbb {R} ^{n}\to \mathbb {R} }$이 실수 벡터에서 실수로 가는 함수라면, ${\displaystyle [f]:[\mathbb {R} ]^{n}\to [\mathbb {R} ]}$는 ${\displaystyle f}$의 구간 확장이라고 불린다. 만약 다음을 만족한다면

${\displaystyle [f]([\mathbf {x} ])\supseteq \{f(\mathbf {y} )\mid \mathbf {y} \in [\mathbf {x} ]\}.}$

구간 확장의 이 정의는 정확한 결과를 제공하지 않는다. 예를 들어, ${\displaystyle [f]([x_{1},x_{2}])=[e^{x_{1}},e^{x_{2}}]}$와 ${\displaystyle [g]([x_{1},x_{2}])=[{-\infty },{\infty }]}$ 모두 지수 함수의 허용 가능한 확장이다. 더 엄밀한 확장이 바람직하지만, 계산 및 부정확성의 상대적 비용을 고려해야 한다. 이 경우, ${\displaystyle [f]}$는 가장 엄밀한 결과를 제공하므로 선택되어야 한다.

실수 표현이 주어졌을 때, 해당 자연 구간 확장은 각 하위 표현, 함수 및 연산자의 구간 확장을 사용하여 달성된다.

테일러 구간 확장(차수 ${\displaystyle k}$)은 ${\displaystyle k+1}$번 미분 가능한 함수 ${\displaystyle f}$로 다음과 같이 정의된다.

${\displaystyle [f]([\mathbf {x} ]):=f(\mathbf {y} )+\sum _{i=1}^{k}{\frac {1}{i!}}\mathrm {D} ^{i}f(\mathbf {y} )\cdot ([\mathbf {x} ]-\mathbf {y} )^{i}+[r]([\mathbf {x} ],[\mathbf {x} ],\mathbf {y} ),}$

어떤 ${\displaystyle \mathbf {y} \in [\mathbf {x} ]}$에 대해, 여기서 ${\displaystyle \mathrm {D} ^{i}f(\mathbf {y} )}$는 점 ${\displaystyle \mathbf {y} }$에서의 ${\displaystyle f}$의 ${\displaystyle i}$차 미분이며, ${\displaystyle [r]}$은 테일러 나머지 항의 구간 확장이다.

${\displaystyle r(\mathbf {x} ,\xi ,\mathbf {y} )={\frac {1}{(k+1)!}}\mathrm {D} ^{k+1}f(\xi )\cdot (\mathbf {x} -\mathbf {y} )^{k+1}.}$

평균값 형태

벡터 ${\displaystyle \xi }$는 ${\displaystyle \mathbf {x} }$와 ${\displaystyle \mathbf {y} }$ 사이에 있으며 ${\displaystyle \mathbf {x} ,\mathbf {y} \in [\mathbf {x} ]}$이고, ${\displaystyle \xi }$는 ${\displaystyle [\mathbf {x} ]}$에 의해 보호된다. 일반적으로 ${\displaystyle \mathbf {y} }$를 구간의 중간점으로 선택하고 자연 구간 확장을 사용하여 나머지를 평가한다.

차수 ${\displaystyle k=0}$인 테일러 구간 확장의 특수한 경우는 평균값 형태라고도 한다.

복소 구간 연산

구간은 중심에서 지정된 거리 내에 있는 점들의 집합으로 정의될 수 있으며, 이 정의는 실수에서 복소수로 확장될 수 있다.^[2] 또 다른 확장은 구간을 복소 평면의 직사각형으로 정의한다. 실수로 계산할 때와 마찬가지로 복소수로 계산할 때도 불확실한 데이터가 관련된다. 따라서 구간 수는 실수 닫힌 구간이고 복소수는 실수 순서쌍이라는 사실을 고려할 때, 구간 연산의 적용을 실수 계산의 불확실성을 측정하는 데만 제한할 이유가 없다.^[3] 따라서 구간 연산은 복소 구간 수를 통해 복소수 계산의 불확실성 영역을 결정하도록 확장될 수 있다. 복소 구간 연산은 직사각형을 사용하거나 원반을 사용하여 정의할 수 있으며, 각각의 장단점이 있다.^[3]

실수 구간 수(실수 닫힌 구간)에 대한 기본 대수 연산은 복소수로 확장될 수 있다. 따라서 복소 구간 연산이 일반 복소 산술과 비슷하지만 같지는 않다는 것은 놀라운 일이 아니다.^[3] 실수 구간 연산의 경우와 마찬가지로, 복소 구간 수의 덧셈과 곱셈 사이에는 특정 특별한 경우를 제외하고 분배 법칙이 성립하지 않으며, 역원이 항상 존재하지 않는다는 것을 보여줄 수 있다.^[3] 일반 복소 산술의 두 가지 유용한 속성, 즉 일반 복소 켤레의 덧셈 및 곱셈 속성은 복소 구간 켤레에는 성립하지 않는다.^[3]

구간 연산은 유사한 방식으로 사원수 및 팔원수와 같은 다른 다차원 수 체계로 확장될 수 있지만, 일반 산술의 다른 유용한 속성을 희생해야 하는 대가가 따른다.^[3]

구간 방법

고전적인 수치해석학 방법은 수치값 간의 의존성을 일반적으로 고려하지 않으므로 구간값 알고리즘으로 일대일 전송될 수 없다.

반올림된 구간 연산

다른 반올림 수준에서의 바깥 경계

실제 구현에서 효과적으로 작동하려면 구간은 부동소수점 계산과 호환되어야 한다. 이전의 연산은 정확한 산술을 기반으로 했지만, 일반적으로 빠른 수치 해법은 사용할 수 없다. ${\displaystyle x\in [0.1,0.8]}$ 및 ${\displaystyle y\in [0.06,0.08]}$에 대한 함수 ${\displaystyle f(x,y)=x+y}$의 값 범위는 예를 들어 ${\displaystyle [0.16,0.88]}$이다. 동일한 계산이 한 자리 정밀도로 수행될 경우, 결과는 일반적으로 ${\displaystyle [0.2,0.9]}$가 된다. 그러나 ${\displaystyle [0.2,0.9]\not \supseteq [0.16,0.88]}$이므로, 이 접근 방식은 ${\displaystyle f([0.1,0.8],[0.06,0.08])}$의 도메인 일부가 손실될 수 있으므로 구간 연산의 기본 원칙에 위배된다. 대신, 바깥쪽으로 반올림된 해인 ${\displaystyle [0.1,0.9]}$가 사용된다.

바이너리 부동소수점 산술에 대한 표준 IEEE 754는 또한 반올림 구현 절차를 규정한다. IEEE 754 호환 시스템은 프로그래머가 가장 가까운 부동소수점 숫자로 반올림하도록 허용한다. 대안으로는 0으로 반올림(절단), 양의 무한대로 반올림(즉, 올림), 또는 음의 무한대로 반올림(즉, 내림)이 있다.

따라서 구간 연산에 필요한 외부 반올림은 상한(올림) 및 하한(내림) 계산 시 프로세서의 반올림 설정을 변경하여 달성할 수 있다. 또는 적절한 작은 구간 ${\displaystyle [\varepsilon _{1},\varepsilon _{2}]}$를 추가할 수 있다.

의존성 문제

값 범위의 근사 추정

소위 "의존성" 문제는 구간 연산 적용의 주요 장애물이다. 구간 방법은 기본 산술 연산 및 함수의 범위를 매우 정확하게 결정할 수 있지만, 더 복잡한 함수에서는 항상 그렇지는 않다. 매개변수를 사용하여 계산에서 구간이 여러 번 나타나고 각 출현이 독립적으로 취해지면, 이는 결과 구간의 불필요한 확장을 초래할 수 있다.

변수의 각 출현을 독립적으로 처리하기

예시로 ${\displaystyle f(x)=x^{2}+x}$로 정의된 함수 ${\displaystyle f}$를 생각해 보자. 구간 ${\displaystyle [-1,1]}$에서 이 함수의 값은 ${\displaystyle \left[-{\tfrac {1}{4}},2\right].}$ 자연 구간 확장으로, 다음과 같이 계산된다.

${\displaystyle [-1,1]^{2}+[-1,1]=[0,1]+[-1,1]=[-1,2],}$

이는 약간 더 크다. 대신 ${\displaystyle x,y\in [-1,1]}$에 대한 함수 ${\displaystyle h(x,y)=x^{2}+y}$의 상한과 하한을 계산했다. 변수 ${\displaystyle x}$가 한 번만 나타나는 ${\displaystyle f}$의 더 나은 표현이 있는데, 즉 ${\displaystyle f(x)=x^{2}+x}$를 이차식에서 덧셈과 제곱으로 다시 쓰는 것이다.

${\displaystyle f(x)=\left(x+{\frac {1}{2}}\right)^{2}-{\frac {1}{4}}.}$

따라서 적절한 구간 계산은

${\displaystyle \left([-1,1]+{\frac {1}{2}}\right)^{2}-{\frac {1}{4}}=\left[-{\frac {1}{2}},{\frac {3}{2}}\right]^{2}-{\frac {1}{4}}=\left[0,{\frac {9}{4}}\right]-{\frac {1}{4}}=\left[-{\frac {1}{4}},2\right]}$

이며 올바른 값을 제공한다.

일반적으로, 각 변수가 한 번만 나타나고 ${\displaystyle f}$가 상자 내에서 연속이면 정확한 값 범위를 얻을 수 있음을 알 수 있다. 그러나 모든 함수를 이런 방식으로 다시 쓸 수는 없다.

래핑 효과

의존성 문제로 인한 값 범위의 과대평가는 넓은 범위를 포괄하여 더 의미 있는 결론을 내리지 못하게 할 수 있다.

범위의 추가 증가는 구간 벡터 형태를 취하지 않는 영역의 해결에서 비롯된다. 선형 시스템의 해 집합은

${\displaystyle {\begin{cases}x=p\\y=p\end{cases}}\qquad p\in [-1,1]}$

정확히 ${\displaystyle (-1,-1)}$과 ${\displaystyle (1,1)}$ 사이의 선이다. 구간 방법을 사용하면 단위 사각형인 ${\displaystyle [-1,1]\times [-1,1]}$이 된다. 이를 래핑 효과라고 한다.

선형 구간 시스템

선형 구간 시스템은 행렬 구간 확장 ${\displaystyle [\mathbf {A} ]\in [\mathbb {R} ]^{n\times m}}$과 구간 벡터 ${\displaystyle [\mathbf {b} ]\in [\mathbb {R} ]^{n}}$로 구성된다. 우리는 모든 벡터에 대해 가장 작은 직육면체 ${\displaystyle [\mathbf {x} ]\in [\mathbb {R} ]^{m}}$를 찾고자 한다. ${\displaystyle \mathbf {x} \in \mathbb {R} ^{m}}$에 대해 ${\displaystyle \mathbf {A} \in [\mathbf {A} ]}$ 및 ${\displaystyle \mathbf {b} \in [\mathbf {b} ]}$를 만족하는 쌍 ${\displaystyle (\mathbf {A} ,\mathbf {b} )}$가 존재한다.

${\displaystyle \mathbf {A} \cdot \mathbf {x} =\mathbf {b} }$.

정사각 시스템(즉, ${\displaystyle n=m}$일 때)의 경우, 모든 가능한 해를 포함하는 그러한 구간 벡터 ${\displaystyle [\mathbf {x} ]}$는 단순히 구간 가우스 방법을 사용하여 찾을 수 있다. 이 방법은 가우스 소거법으로 알려진 선형 대수 방법을 구간 버전으로 대체하여 수치 연산을 수행한다. 그러나 이 방법은 계산에서 구간 엔티티 ${\displaystyle [\mathbf {A} ]}$와 ${\displaystyle [\mathbf {b} ]}$를 반복적으로 사용하기 때문에 일부 문제에 대해 좋지 않은 결과를 생성할 수 있다. 따라서 구간 값 가우스 방법의 결과는 전체 해 집합을 포함하지만, 그 바깥에도 넓은 영역을 가지고 있기 때문에 단지 초기 거친 추정치만을 제공한다.

거친 해 ${\displaystyle [\mathbf {x} ]}$는 가우스-자이델 방법의 구간 버전을 사용하여 종종 개선될 수 있다. 이에 대한 동기는 선형 방정식의 구간 확장인 ${\displaystyle i}$번째 행이다.

${\displaystyle {\begin{pmatrix}{[a_{11}]}&\cdots &{[a_{1n}]}\\\vdots &\ddots &\vdots \\{[a_{n1}]}&\cdots &{[a_{nn}]}\end{pmatrix}}\cdot {\begin{pmatrix}{x_{1}}\\\vdots \\{x_{n}}\end{pmatrix}}={\begin{pmatrix}{[b_{1}]}\\\vdots \\{[b_{n}]}\end{pmatrix}}}$

는 ${\displaystyle 1/[a_{ii}]}$ 나눗셈이 허용된다면 변수 ${\displaystyle x_{i}}$에 의해 결정될 수 있다. 따라서 동시에 다음을 만족한다.

${\displaystyle x_{j}\in [x_{j}]}$ and ${\displaystyle x_{j}\in {\frac {[b_{i}]-\sum \limits _{k\not =j}[a_{ik}]\cdot [x_{k}]}{[a_{ii}]}}}$.

따라서 이제 ${\displaystyle [x_{j}]}$를 다음으로 바꿀 수 있다.

${\displaystyle [x_{j}]\cap {\frac {[b_{i}]-\sum \limits _{k\not =j}[a_{ik}]\cdot [x_{k}]}{[a_{ii}]}}}$,

그리고 벡터 ${\displaystyle [\mathbf {x} ]}$는 각 요소에 의해. 이 절차는 대각지배행렬에 대해 더 효율적이기 때문에 시스템 ${\displaystyle [\mathbf {A} ]\cdot \mathbf {x} =[\mathbf {b} ]{\mbox{,}}}$ 대신 적절한 유리 행렬 ${\displaystyle \mathbf {M} }$을 곱하여 결과 행렬 방정식으로 만들 수 있다.

${\displaystyle (\mathbf {M} \cdot [\mathbf {A} ])\cdot \mathbf {x} =\mathbf {M} \cdot [\mathbf {b} ]}$

를 해결하도록 남겨둔다. 예를 들어, ${\displaystyle [\mathbf {A} ]}$ 내의 중앙 행렬 ${\displaystyle \mathbf {A} }$에 대해 ${\displaystyle \mathbf {M} =\mathbf {A} ^{-1}}$을 선택하면 ${\displaystyle \mathbf {M} \cdot [\mathbf {A} ]}$는 항등 행렬의 외부 확장이 된다.

이러한 방법들은 발생하는 구간의 폭이 충분히 작을 때만 잘 작동한다. 더 넓은 구간의 경우, 구간-선형 시스템을 유한한(비록 크지만) 실수 동등 선형 시스템에 사용하는 것이 유용할 수 있다. 만약 모든 행렬 ${\displaystyle \mathbf {A} \in [\mathbf {A} ]}$가 역행렬을 가진다면, 구간에 나타나는 끝점의 모든 가능한 조합(상단 및 하단)을 고려하는 것으로 충분하다. 결과 문제는 재래식 수치 방법으로 해결할 수 있다. 구간 연산은 여전히 반올림 오차를 결정하는 데 사용된다.

이는 작은 차원의 시스템에만 적합하다. 왜냐하면 완전히 채워진 ${\displaystyle n\times n}$ 행렬의 경우 ${\displaystyle 2^{n^{2}}}$개의 실제 행렬을 역전시켜야 하며, 오른쪽에는 ${\displaystyle 2^{n}}$개의 벡터가 필요하기 때문이다. 이 접근법은 이르지 론이 개발했으며 현재도 개발 중이다.^[4]

구간 뉴턴 방법

"두꺼운" 함수에서 구간 뉴턴 단계에서의 검색 영역 축소.

구간 벡터 ${\displaystyle [\mathbf {x} ]}$에서 0을 찾는 뉴턴 방법의 구간 변형은 평균값 확장으로부터 유도될 수 있다.^[5] ${\displaystyle \mathbf {y} \in [\mathbf {x} ]}$에 적용되는 미지의 벡터 ${\displaystyle \mathbf {z} \in [\mathbf {x} ]}$에 대해 다음과 같다.

${\displaystyle f(\mathbf {z} )\in f(\mathbf {y} )+[J_{f}](\mathbf {[x]} )\cdot (\mathbf {z} -\mathbf {y} )}$.

0 ${\displaystyle \mathbf {z} }$에 대해, 즉 ${\displaystyle f(z)=0}$이므로 다음을 만족해야 한다.

${\displaystyle f(\mathbf {y} )+[J_{f}](\mathbf {[x]} )\cdot (\mathbf {z} -\mathbf {y} )=0}$.

이는 다음 식과 동등하다. ${\displaystyle \mathbf {z} \in \mathbf {y} -[J_{f}](\mathbf {[x]} )^{-1}\cdot f(\mathbf {y} )}$. ${\displaystyle [J_{f}](\mathbf {[x]} )^{-1}\cdot f(\mathbf {y} ))}$의 외부 추정은 선형 방법을 사용하여 결정될 수 있다.

구간 뉴턴 방법의 각 단계에서 근사 시작 값 ${\displaystyle [\mathbf {x} ]\in [\mathbb {R} ]^{n}}$은 ${\displaystyle [\mathbf {x} ]\cap \left(\mathbf {y} -[J_{f}](\mathbf {[x]} )^{-1}\cdot f(\mathbf {y} )\right)}$로 대체되며, 따라서 결과는 개선될 수 있다. 전통적인 방법과 달리 구간 방법은 0을 포함함으로써 결과에 접근한다. 이는 결과가 초기 범위의 모든 0을 생성함을 보장한다. 반대로, 뉴턴 단계가 빈 집합을 생성하면 ${\displaystyle f}$의 0이 초기 범위 ${\displaystyle [\mathbf {x} ]}$에 없었음을 증명한다.

이 방법은 시작 영역 내의 모든 영점에 수렴한다. 0으로 나누면 뚜렷한 영점들이 분리될 수 있지만, 분리가 완전하지 않을 수 있다. 이는 이분법으로 보완할 수 있다.

예를 들어, 함수 ${\displaystyle f(x)=x^{2}-2}$, 시작 범위 ${\displaystyle [x]=[-2,2]}$, 점 ${\displaystyle y=0}$을 고려해 보자. 그러면 ${\displaystyle J_{f}(x)=2\,x}$이고 첫 번째 뉴턴 단계는 다음을 제공한다.

${\displaystyle [-2,2]\cap \left(0-{\frac {1}{2\cdot [-2,2]}}(0-2)\right)=[-2,2]\cap {\Big (}[{-\infty },{-0.5}]\cup [{0.5},{\infty }]{\Big )}=[{-2},{-0.5}]\cup [{0.5},{2}]}$.

더 많은 뉴턴 단계는 ${\displaystyle x\in [{-2},{-0.5}]}$와 ${\displaystyle [{0.5},{2}]}$에 대해 별도로 사용된다. 이들은 ${\displaystyle -{\sqrt {2}}}$와 ${\displaystyle +{\sqrt {2}}}$ 주위의 임의로 작은 구간으로 수렴한다.

구간 뉴턴 방법은 ${\displaystyle g(x)=x^{2}-[2,3]}$과 같은 두꺼운 함수에도 사용할 수 있으며, 이 경우에도 구간 결과가 나온다. 그러면 결과는 ${\displaystyle \left[-{\sqrt {3}},-{\sqrt {2}}\right]\cup \left[{\sqrt {2}},{\sqrt {3}}\right]}$를 포함하는 구간을 생성한다.

이분법과 덮개

"다짐"을 통해 개선된 거친 추정치(청록색) 및 추정치(빨간색)

다양한 구간 방법은 서로 다른 구간 확장의 크기 간의 종속성을 고려하지 않으므로 보수적인 결과를 제공한다. 그러나 종속성 문제는 더 좁은 구간에서는 덜 중요해진다.

구간 벡터 ${\displaystyle [\mathbf {x} ]}$를 더 작은 상자들 ${\displaystyle [\mathbf {x} _{1}],\ldots ,[\mathbf {x} _{k}],}$로 덮어서

${\displaystyle [\mathbf {x} ]=\bigcup _{i=1}^{k}[\mathbf {x} _{i}],}$

는 값 범위에 대해 유효하다.

${\displaystyle f([\mathbf {x} ])=\bigcup _{i=1}^{k}f([\mathbf {x} _{i}]).}$

따라서 위에서 설명한 구간 확장에 대해 다음이 성립한다.

${\displaystyle [f]([\mathbf {x} ])\supseteq \bigcup _{i=1}^{k}[f]([\mathbf {x} _{i}]).}$

${\displaystyle [f]([\mathbf {x} ])}$는 종종 우변의 진정한 상위 집합이므로, 이는 일반적으로 개선된 추정으로 이어진다.

이러한 덮개는 이분법으로 생성될 수 있는데, 구간 벡터 ${\displaystyle [\mathbf {x} ]=([x_{11},x_{12}],\ldots ,[x_{n1},x_{n2}])}$의 두꺼운 요소 ${\displaystyle [x_{i1},x_{i2}]}$를 중앙에서 ${\displaystyle \left[x_{i1},{\tfrac {1}{2}}(x_{i1}+x_{i2})\right]}$와 ${\displaystyle \left[{\tfrac {1}{2}}(x_{i1}+x_{i2}),x_{i2}\right]}$ 두 구간으로 분할하는 것이다. 결과가 여전히 적절하지 않으면 추가적인 점진적 세분화가 가능하다. ${\displaystyle r}$개의 벡터 요소 분할로부터 ${\displaystyle 2^{r}}$개의 구간 덮개가 생성되어 계산 비용이 크게 증가한다.

매우 넓은 간격의 경우, 모든 간격을 일정한(그리고 더 작은) 폭을 가진 여러 하위 간격으로 나누는 것이 도움이 될 수 있는데, 이를 마이닝(mincing)이라고 한다. 이렇게 하면 중간 이분법 단계에 대한 계산을 피할 수 있다. 두 가지 방법 모두 저차원 문제에만 적합하다.

응용

구간 연산은 집합 반전, 운동 계획, 집합 추정 또는 안정성 분석과 같은 다양한 영역에서 정확한 수치값이 없는 추정치를 다루는 데 사용될 수 있다.^[6]

반올림 오차 분석

구간 연산은 오차 분석과 함께 각 계산에서 발생하는 반올림 오차를 제어하는 데 사용된다. 구간 연산의 장점은 각 연산 후에 실제 결과를 신뢰할 수 있게 포함하는 구간이 존재한다는 것이다. 구간 경계 간의 거리는 반올림 오차의 현재 계산을 직접 제공한다.

오차 = 주어진 구간 ${\displaystyle [a,b]}$에 대해 ${\displaystyle \mathrm {abs} (a-b)}$.

구간 분석은 피벗과 같은 기존의 오차 감소 방법을 대체하는 것이 아니라 보완한다.

공차 분석

기술 및 물리적 프로세스 시뮬레이션 중에는 정확한 수치를 할당할 수 없는 매개변수가 자주 발생한다. 기술 구성 요소의 생산 공정은 특정 공차를 허용하므로 일부 매개변수는 구간 내에서 변동한다. 또한 많은 기본 상수는 정확하게 알려져 있지 않다.^[1]

만약 이러한 공차의 영향을 받는 시스템의 동작이 예를 들어, ${\displaystyle \mathbf {p} \in [\mathbf {p} ]}$에 대해 ${\displaystyle f(\mathbf {x} ,\mathbf {p} )=0}$을 만족하고 ${\displaystyle \mathbf {x} }$가 알려지지 않은 경우, 가능한 해의 집합은 다음과 같다.

${\displaystyle \{\mathbf {x} \,|\,\exists \mathbf {p} \in [\mathbf {p} ],f(\mathbf {x} ,\mathbf {p} )=0\}}$,

구간 방법을 통해 찾을 수 있다. 이는 전통적인 오차 전파 분석에 대한 대안을 제공한다. 몬테카를로 시뮬레이션과 같은 점(point) 방법과 달리, 구간 연산 방법론은 해 영역의 어떤 부분도 간과되지 않음을 보장한다. 그러나 다른 확률 기반 분포는 고려되지 않으므로 결과는 항상 오차 분포에 대한 최악의 경우 분석이다.

퍼지 구간 연산

일련의 구간에 의한 정규 분포의 근사

구간 연산은 퍼지 논리에 사용되는 퍼지 양에 대한 소속 함수와 함께 사용할 수도 있다. 엄격한 ${\displaystyle x\in [x]}$ 및 ${\displaystyle x\not \in [x]}$ 진술 외에도, ${\displaystyle [0,1]}$ 범위의 실수 ${\displaystyle \mu }$가 할당되는 중간 값도 가능하다. ${\displaystyle \mu =1}$은 확실한 멤버십에 해당하고 ${\displaystyle \mu =0}$은 비멤버십이다. 분포 함수는 불확실성을 할당하며, 이는 추가 구간으로 이해될 수 있다.

퍼지 산술^[7]의 경우, 유한한 수의 이산적인 소속 단계 ${\displaystyle \mu _{i}\in [0,1]}$만 고려된다. 불분명한 값에 대한 그러한 분포의 형태는 일련의 구간으로 표현될 수 있다.

${\displaystyle \left[x^{(1)}\right]\supset \left[x^{(2)}\right]\supset \cdots \supset \left[x^{(k)}\right].}$

구간 ${\displaystyle \left[x^{(i)}\right]}$는 단계 ${\displaystyle \mu _{i}}$에 대한 변동 범위와 정확히 일치한다.

불분명한 값 ${\displaystyle x_{1},\ldots ,x_{n}}$ 및 해당 시퀀스에 대한 함수 ${\displaystyle f(x_{1},\ldots ,x_{n})}$의 적절한 분포는 다음과 같다.

${\displaystyle \left[x_{1}^{(1)}\right]\supset \cdots \supset \left[x_{1}^{(k)}\right],\ldots ,\left[x_{n}^{(1)}\right]\supset \cdots \supset \left[x_{n}^{(k)}\right]}$

는 시퀀스에 의해 근사화될 수 있다.

${\displaystyle \left[y^{(1)}\right]\supset \cdots \supset \left[y^{(k)}\right],}$

여기서

${\displaystyle \left[y^{(i)}\right]=f\left(\left[x_{1}^{(i)}\right],\ldots \left[x_{n}^{(i)}\right]\right)}$

이며, 구간 방법을 통해 계산할 수 있다. 값 ${\displaystyle \left[y^{(1)}\right]}$은 구간 계산의 결과에 해당한다.

컴퓨터 보조 증명

워릭 터커는 스메일의 문제 중 14번째, 즉 로렌츠 끌개가 기묘한 끌개임을 보이기 위해 구간 연산을 사용했다.^[8] 토머스 캘리스터 헤일스는 케플러의 추측을 해결하기 위해 구간 연산을 사용했다.

교환법칙, 결합법칙

덧셈과 곱셈에 대하여 교환법칙과 결합법칙이 성립한다. 즉

A + B = B + A, A·B = B·A

(A + B) + C = A + (B + C), (A·B)·C = A·(B·C)

분배법칙

분배법칙은 일반적으로 성립하지 않는다.

${\displaystyle {\begin{matrix}[a,b]\cdot ([c,d]-[e,f])&=&[a,b]\cdot [c-f,d-e]\\&=&[min(a(c-f),a(d-e),b(c-f),b(d-e)),max(a(c-f),a(d-e),b(c-f),b(d-e))]\end{matrix}}}$

${\displaystyle [a,b]\cdot [c,d]-[a,b]\cdot [e,f]=[min(ac,ad,bc,bd)]-[max(ac,ad,bc,bd)]-[min(ae,af,be,bf)]-[max(ae,af,be,bf)]}$

결과가 서로 다르다.

역사

구간 연산은 수학에서 완전히 새로운 현상이 아니다. 역사상 여러 번 다른 이름으로 나타났다. 예를 들어, 아르키메데스는 기원전 3세기에 223/71 < π < 22/7의 하한과 상한을 계산했다. 실제로 구간을 이용한 계산은 다른 수치 기술만큼 인기를 얻지 못했지만 완전히 잊히지도 않았다.

구간 및 실수의 다른 부분집합을 계산하는 규칙은 1931년 로절린드 시실리 영의 저서에 발표되었다.^[9] 디지털 시스템의 신뢰성을 향상시키기 위한 범위 숫자에 대한 산술 작업은 1951년 파울 S. 드와이어([[:de:{{{3}}}|독일어판]])의 선형 대수 교과서에 발표되었다.^[10] 구간은 부동소수점 숫자와 관련된 반올림 오차를 측정하는 데 사용되었다. 수치해석학에서의 구간 대수에 대한 포괄적인 논문은 스나가 테루오 (1958)에 의해 발표되었다.^[11]

현대 구간 연산의 탄생은 1966년 레이먼 E. 무어의 책 "구간 분석"의 출현으로 특징지어진다.^[12][13] 그는 1958년 봄에 아이디어를 얻었고, 1년 후 컴퓨터 구간 연산에 대한 논문을 발표했다.^[14] 그의 공로는 단순한 원리에서 시작하여 반올림으로 인한 오차뿐만 아니라 자동화된 오차 분석을 위한 일반적인 방법을 제공했다는 점이다.

1956년, 미에치스와프 바르무스는 독립적으로 구간 계산 공식을 제안했지만,^[15] 무어는 첫 번째 비자명한 응용을 발견했다.

그 후 20년 동안, 독일 연구 그룹은 울리히 W. 쿨리쉬^[16][17]와 괴츠 알레펠트([[:de:{{{3}}}|독일어판]])^[18]를 중심으로 카를스루에 대학교에서, 그리고 나중에는 베르기셰 부퍼탈 대학교에서도 선구적인 연구를 수행했다. 예를 들어, 카를 니켈([[:de:{{{3}}}|독일어판]])은 더 효과적인 구현을 탐구했으며, 방정식 시스템의 해 집합에 대한 개선된 포함 절차는 아놀드 노이마이어 등이 개발했다. 1960년대에는 엘돈 R. 한센이 선형 방정식의 구간 확장을 다루었고, 이후 전역 최적화에 중요한 기여를 했으며, 현재는 한센의 방법으로 알려진 가장 널리 사용되는 구간 알고리즘을 포함한다.^[5] 이 분야의 고전적인 방법은 종종 가장 큰(또는 가장 작은) 전역 값을 결정하는 데 문제가 있었지만, 지역 최적값만 찾을 수 있었고 더 나은 값을 찾을 수 없었다. 헬무트 랏쉐크와 존 조지 로크네는 분기 한정법을 개발했으며, 이는 그 전까지는 정수 값에만 적용되었으나 구간을 사용하여 연속 값에 대한 응용을 제공했다.

1988년에 루돌프 로너는 상미분 방정식을 사용하는 초기값 문제에 대한 신뢰할 수 있는 해법을 위한 포트란 기반 소프트웨어를 개발했다.^[19]

Reliable Computing(원래 Interval Computations) 저널은 1990년대부터 출판되었으며, 컴퓨터 보조 계산의 신뢰성에 전념하고 있다. 수석 편집자 R. 베이커 키어포트(R. Baker Kearfott)는 전역 최적화에 대한 연구 외에도 구간 연산에 사용되는 표기법과 용어를 통일하는 데 상당한 기여를 했다.^[20]

최근 몇 년간, 프랑스 소피아앙티폴리스의 INRIA COPRIN 연구 그룹은 특히 매개변수 함수의 역상 추정 및 강건 제어 이론에 집중해 왔다.^[21]

구현

구간 연산을 사용하여 수치 응용 프로그램을 개발할 수 있도록 해주는 많은 소프트웨어 패키지가 있다.^[22] 이들은 일반적으로 프로그램 라이브러리 형태로 제공된다. 또한 언어 확장으로 구간 자료형과 적절한 연산을 처리하는 C++ 및 포트란 컴파일러도 있어 구간 연산이 직접 지원된다.

1967년부터 카를스루에 대학교에서 C++, 포트란, 파스칼 등 다양한 프로그래밍 언어를 위한 XSC(Extensions for Scientific Computation)가 개발되었다.^[23] 첫 번째 플랫폼은 Zuse Z23이었으며, 이를 위해 적절한 기본 연산자와 함께 새로운 구간 자료형이 제공되었다. 이어서 1976년에는 자일로그 Z80에서 자동화된 결과 검증을 위한 빠르고 복잡한 루틴을 만들 수 있게 해주는 파스칼 변형인 Pascal-SC가 출시되었다. 그 다음에는 IBM이 나중에 제공한 System/370 아키텍처용 Fortran 77 기반 ACRITH-XSC(FORTRAN-SC)가 나왔다. 1991년부터는 Pascal-XSC로 C 컴파일러용 코드를 생성할 수 있었고, 1년 후 C++ 클래스 라이브러리는 다양한 컴퓨터 시스템에서 C-XSC를 지원했다. 1997년, 모든 XSC 변형은 GNU 일반 공중 사용 허가서 아래에서 사용할 수 있게 되었다. 2000년 초, 개선된 C++ 표준에 맞춰 베르기셰 부퍼탈 대학교 과학 계산 연구 그룹의 주도하에 C-XSC 2.0이 출시되었다.

또 다른 C++ 클래스 라이브러리는 1993년 함부르크 공과대학교에서 Profil/BIAS(Programmer's Runtime Optimized Fast Interval Library, Basic Interval Arithmetic)라는 이름으로 만들어졌는데, 이는 일반적인 구간 연산을 사용자에게 더 편리하게 만들었다. 이 라이브러리는 하드웨어의 효율적인 사용, 이식성, 특정 구간 표현 방식에 대한 독립성을 강조했다.

Boost 컬렉션의 C++ 라이브러리에는 구간을 위한 템플릿 클래스가 포함되어 있다. 그 저자들은 C++ 표준 언어에 구간 연산을 포함시키려는 목표를 가지고 있다.^[24]

프링크 (프로그래밍 언어)에는 임의 정밀도 산술을 처리하는 구간 연산 구현이 있다. 프링크로 작성된 프로그램은 다시 작성하거나 재컴파일할 필요 없이 구간을 사용할 수 있다.

GAOL^[25]은 또 다른 C++ 구간 연산 라이브러리인데, 제약 프로그래밍에 사용되는 관계형 구간 연산자를 제공한다는 점에서 독특하다.

무어 라이브러리^[26]는 C++로 구현된 효율적인 구간 연산 구현체이다. 이 라이브러리는 임의 정밀도의 끝점을 가진 구간을 제공하며 C++의 개념 기능을 기반으로 한다.

줄리아 (프로그래밍 언어)^[27]는 ValidatedNumerics.jl 패키지를 통해 구간 연산 구현과 근 찾기(실수 및 복소수 값 함수 모두) 및 구간 제약 프로그래밍과 같은 고급 기능을 제공한다.^[28]

또한 오일러 수학 도구 상자, 프리카스, 메이플, 매스매티카, 맥시마^[29] 및 뮤패드와 같은 컴퓨터 대수 시스템도 구간을 처리할 수 있다. 매트랩 확장인 Intlab^[30]은 BLAS 루틴을 기반으로 하며, 도구 상자 b4m은 Profil/BIAS 인터페이스를 만든다.^[30][31]

함수형 언어 OCaml용 라이브러리는 어셈블리어와 C로 작성되었다.^[32]

MPFI는 임의 정밀도 구간 연산을 위한 라이브러리로, C로 작성되었으며 MPFR을 기반으로 한다.^[33]

IEEE 1788 표준

구간 연산에 대한 표준인 IEEE Std 1788-2015는 2015년 6월에 승인되었다.^[34] 두 가지 참조 구현이 무료로 제공된다.^[35] 이들은 표준 작업 그룹 구성원들이 개발했다. C++용 libieeep1788^[36] 라이브러리와 GNU 옥타브용 interval 패키지^[37]이다.

표준의 최소 부분집합인 IEEE Std 1788.1-2017은 2017년 12월에 승인되어 2018년 2월에 출판되었다. 이는 구현하기 더 쉽고 구현 생산을 가속화할 수 있을 것으로 예상된다.^[38]

컨퍼런스 및 워크숍

매년 전 세계에서 여러 국제 컨퍼런스 또는 워크숍이 개최된다. 주요 컨퍼런스는 아마도 SCAN(과학 컴퓨팅, 컴퓨터 산술 및 검증된 수치 계산 국제 심포지엄)이지만, SWIM(구간 방법 소규모 워크숍), PPAM(병렬 처리 및 응용 수학 국제 컨퍼런스), REC(신뢰할 수 있는 엔지니어링 컴퓨팅 국제 워크숍)도 있다.

같이 보기

• 아핀 산술
• INTLAB (구간 연구실)
• 자동 미분
• 다중 격자 방법
• 몬테카를로 시뮬레이션
• 구간 유한 요소
• 퍼지 수
• 유효숫자
• 카를스루에 정확한 산술 (KAA)
• 유넘