기수 트리

컴퓨터 과학에서 기수 트리, 래딕스 트리(radix tree) 또는 기수 트라이(radix trie) 또는 압축 접두사 트리(compact prefix tree) 또는 압축 트라이(compressed trie)는 유일한 자식인 각 노드가 부모와 병합되는 공간 최적화된 트라이 (접두사 트리)를 나타내는 자료 구조이다. 그 결과 모든 내부 노드의 자식 수는 기수 트리의 기수 r 이하이며, 여기서 r = 2^x (일부 정수 x ≥ 1). 일반 트리와 달리 엣지는 단일 요소뿐만 아니라 요소 시퀀스로도 레이블을 지정할 수 있다. 이로 인해 기수 트리는 작은 집합 (특히 문자열이 긴 경우) 및 긴 접두사를 공유하는 문자열 집합에 훨씬 더 효율적이다.

피터 파이퍼 혀 꼬는 말의 단어 기수 트리 예시

일반 트리(전체 키가 불일치 지점까지 시작부터 한꺼번에 비교됨)와 달리, 각 노드의 키는 비트 덩어리별로 비교되며, 해당 노드의 해당 덩어리에 있는 비트의 양은 기수 트라이의 기수 r이다. r이 2일 때, 기수 트라이는 이진(즉, 해당 노드의 키의 1비트 부분을 비교)이며, 이는 트라이 깊이를 최대화하는 대신 희소성을 최소화한다. 즉, 키에서 분기하지 않는 비트 문자열의 혼동까지 최대화한다. r ≥ 4가 2의 거듭제곱일 때, 기수 트라이는 r-진 트라이이며, 이는 잠재적 희소성을 희생하여 기수 트라이의 깊이를 줄인다.

최적화로서, 엣지 레이블은 문자열에 대한 두 개의 포인터(첫 번째 및 마지막 요소용)를 사용하여 상수 크기로 저장할 수 있다.^[1]

이 문서의 예시에서는 문자열을 문자 시퀀스로 보여주지만, 문자열 요소의 유형은 임의로 선택할 수 있다. 예를 들어, 멀티바이트 문자 인코딩 또는 유니코드를 사용할 때 문자열 표현의 비트 또는 바이트로 선택할 수 있다.

응용 분야

기수 트리는 문자열로 표현할 수 있는 키를 가진 연관 배열을 구성하는 데 유용하다. 이들은 IP 라우팅 영역에서 특히 응용된다.^[2][3][4] 여기서 몇 가지 예외를 제외하고 광범위한 값을 포함할 수 있는 능력은 IP 주소의 계층적 구성에 특히 적합하다.^[5] 또한 정보 검색에서 텍스트 문서의 역색인에도 사용된다.

연산

기수 트리는 삽입, 삭제 및 검색 연산을 지원한다. 삽입은 트리에 새 문자열을 추가하면서 저장되는 데이터 양을 최소화하려고 시도한다. 삭제는 트리에서 문자열을 제거한다. 검색 연산에는 (반드시 제한되지는 않지만) 정확한 조회, 선행 요소 찾기, 후행 요소 찾기 및 접두사가 있는 모든 문자열 찾기가 포함된다. 이 모든 연산은 O(k)이며, 여기서 k는 집합의 모든 문자열의 최대 길이이고, 길이는 기수 트라이의 기수와 동일한 비트 수로 측정된다.

조회

패트리샤 트라이에서 문자열을 찾는 방법의 예

조회 연산은 트라이에 문자열이 존재하는지 확인한다. 대부분의 연산은 특정 작업을 처리하기 위해 이 접근 방식을 어떤 식으로든 수정한다. 예를 들어, 문자열이 끝나는 노드가 중요할 수 있다. 이 연산은 일부 엣지가 여러 요소를 소비한다는 점을 제외하고 트라이와 유사하다.

다음 의사 코드는 이러한 메서드와 멤버가 존재한다고 가정한다.

엣지

• 노드 targetNode
• 문자열 label

노드

• 엣지 배열 edges
• 함수 isLeaf()

함수 lookup(문자열 x)
{
    // 요소를 찾지 않은 채 루트에서 시작
    노드 traverseNode := root;
    정수 elementsFound := 0;

    // 리프를 찾거나 계속 진행할 수 없을 때까지 순회
    while (traverseNode != null && !traverseNode.isLeaf() && elementsFound < x.length)
    {
        // x에서 아직 찾지 못한 요소를 기반으로 탐색할 다음 엣지 가져오기
        엣지 nextEdge := 선택 edge
                         from traverseNode.edges
                         where edge.label is a prefix of x.suffix(elementsFound)
            // x.suffix(elementsFound)는 x의 마지막 (x.length - elementsFound) 요소를 반환

        // 엣지를 찾았는가?
        if (nextEdge != null)
        {
            // 탐색할 다음 노드 설정
            traverseNode := nextEdge.targetNode;

            // 엣지에 저장된 레이블을 기반으로 찾은 요소 증가
            elementsFound += nextEdge.label.length;
        }
        else
        {
            // 루프 종료
            traverseNode := null;
        }
    }

    // 리프 노드에 도달했고 정확히 x.length 요소를 사용했다면 일치하는 것을 찾은 것
    return (traverseNode != null && traverseNode.isLeaf() && elementsFound == x.length);
}

삽입

문자열을 삽입하려면 더 이상 진행할 수 없을 때까지 트리를 검색한다. 이 시점에서 우리는 입력 문자열의 나머지 모든 요소로 레이블이 지정된 새 나가는 엣지를 추가하거나, 나머지 입력 문자열과 접두사를 공유하는 나가는 엣지가 이미 있는 경우, 이를 두 개의 엣지(처음 것은 공통 접두사로 레이블 지정됨)로 분할하고 진행한다. 이 분할 단계는 어떤 노드도 가능한 문자열 요소보다 많은 자식을 갖지 않도록 보장한다.

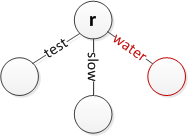
삽입의 여러 경우가 아래에 나와 있다. r은 단순히 루트를 나타낸다. 엣지는 필요한 경우 문자열을 종료하기 위해 빈 문자열로 레이블을 지정할 수 있으며 루트에는 들어오는 엣지가 없다고 가정한다. (위에서 설명한 조회 알고리즘은 빈 문자열 엣지를 사용할 때 작동하지 않는다.)

• 
  루트에 'water' 삽입
• 
  'slow'를 유지하면서 'slower' 삽입
• 
  'tester'의 접두사인 'test' 삽입
• 
  'test'를 분할하고 새 엣지 레이블 'st'를 생성하면서 'team' 삽입
• 
  'te'를 분할하고 이전 문자열을 한 레벨 아래로 이동하면서 'toast' 삽입

삭제

트리에서 문자열 x를 삭제하려면 먼저 x를 나타내는 리프를 찾는다. 그런 다음 x가 존재한다고 가정하고 해당 리프 노드를 제거한다. 리프 노드의 부모에게 다른 자식이 하나만 있는 경우 해당 자식의 들어오는 레이블이 부모의 들어오는 레이블에 추가되고 자식이 제거된다.

추가 연산

• 공통 접두사를 가진 모든 문자열 찾기: 동일한 접두사로 시작하는 문자열 배열을 반환한다.
• 선행 요소 찾기: 사전순으로 주어진 문자열보다 작은 가장 큰 문자열을 찾는다.
• 후행 요소 찾기: 사전순으로 주어진 문자열보다 큰 가장 작은 문자열을 찾는다.

역사

이 자료 구조는 1968년 도널드 모리슨^[6]과 게르노트 그베헨베르거가 발명했으며,^[7] 주로 모리슨과 관련이 있다.

도널드 커누스는 《컴퓨터 프로그래밍의 예술》 3권 498-500페이지에서 이들을 "패트리샤의 트리"라고 불렀는데, 이는 모리슨 논문의 제목에 있는 약어("PATRICIA - Practical Algorithm to Retrieve Information Coded in Alphanumeric")에서 따온 것으로 추정된다. 오늘날 패트리샤 트리는 기수가 2인 기수 트리로 간주된다. 즉, 키의 각 비트가 개별적으로 비교되고 각 노드는 양방향(즉, 왼쪽 대 오른쪽) 분기이다.

다른 자료 구조와의 비교

(다음 비교에서는 키의 길이가 k이고 자료 구조에 n개의 멤버가 있다고 가정한다.)

균형 트리와 달리 기수 트리는 O(log n) 시간 대신 O(k) 시간에 조회, 삽입 및 삭제를 허용한다. 이는 일반적으로 k ≥ log n이므로 장점처럼 보이지 않지만, 균형 트리에서는 모든 비교가 O(k) 최악의 시간 복잡도를 요구하는 문자열 비교이며, 이 중 많은 부분이 긴 공통 접두사(비교가 문자열의 시작 부분에서 시작하는 경우) 때문에 실제로는 느리다. 트라이에서는 모든 비교가 상수 시간을 요구하지만, 길이가 m인 문자열을 조회하는 데 m번의 비교가 필요하다. 기수 트리는 더 적은 비교로 이러한 연산을 수행할 수 있으며, 훨씬 더 적은 노드를 요구한다.

그러나 기수 트리는 트라이의 단점도 공유한다. 요소 문자열 또는 문자열로 효율적으로 가역적으로 매핑되는 요소에만 적용될 수 있으므로, 전순서를 가진 모든 데이터 형식에 적용되는 균형 탐색 트리의 완전한 일반성이 부족하다. 문자열로의 가역 매핑은 균형 탐색 트리에 필요한 전순서를 생성하는 데 사용될 수 있지만, 그 반대는 불가능하다. 이는 데이터 형식이 비교 연산만 제공하고 (역)직렬화 연산은 제공하지 않는 경우에도 문제가 될 수 있다.

해시 테이블은 일반적으로 예상 O(1) 삽입 및 삭제 시간을 갖는다고 하지만, 이는 키의 해시 계산을 상수 시간 연산으로 간주할 때만 해당된다. 키 해싱을 고려하면 해시 테이블은 예상 O(k) 삽입 및 삭제 시간을 가지지만, 충돌 처리 방식에 따라 최악의 경우 더 오래 걸릴 수 있다. 기수 트리는 최악의 경우 O(k) 삽입 및 삭제를 갖는다. 기수 트리의 후행/선행 연산은 해시 테이블에서 구현되지 않는다.

변형

기수 트리의 일반적인 확장은 "검정"과 "흰색"의 두 가지 노드 색상을 사용한다. 주어진 문자열이 트리에 저장되어 있는지 확인하려면 맨 위에서부터 검색을 시작하여 더 이상 진행할 수 없을 때까지 입력 문자열의 엣지를 따라간다. 검색 문자열이 소모되고 최종 노드가 검정 노드이면 검색이 실패한 것이다. 흰색이면 검색이 성공한 것이다. 이를 통해 공통 접두사를 가진 광범위한 문자열을 흰색 노드를 사용하여 트리에 추가한 다음, 검정 노드를 사용하여 작은 예외 집합을 공간 효율적인 방식으로 제거할 수 있다.

HAT-트라이는 기수 트리를 기반으로 하는 캐시 인식 자료 구조로, 효율적인 문자열 저장 및 검색, 그리고 순서 있는 반복을 제공한다. 시간과 공간 모두에서 성능은 캐시 인식 해시 테이블과 비교할 만하다.^[8][9]

PATRICIA 트라이는 기수 2(이진) 트라이의 특수 변형으로, 모든 키의 모든 비트를 명시적으로 저장하는 대신, 노드는 두 하위 트리를 구별하는 첫 번째 비트의 위치만 저장한다. 순회 동안 알고리즘은 검색 키의 인덱싱된 비트를 검사하고 적절하게 왼쪽 또는 오른쪽 하위 트리를 선택한다. PATRICIA 트라이의 주목할 만한 특징은 저장된 고유 키마다 하나의 노드만 삽입하면 되므로 PATRICIA가 표준 이진 트라이보다 훨씬 더 간결하다는 것이다. 또한 실제 키가 더 이상 명시적으로 저장되지 않으므로 일치 여부를 확인하기 위해 인덱싱된 레코드에 대해 전체 키 비교를 한 번 수행해야 한다. 이러한 점에서 PATRICIA는 해시 테이블을 사용한 인덱싱과 특정 유사성을 가진다.^[6]

적응형 기수 트리는 기수 트리에 적응형 노드 크기를 통합한 기수 트리 변형이다. 일반적인 기수 트리의 주요 단점 중 하나는 모든 레벨에서 일정한 노드 크기를 사용하기 때문에 공간 사용이다. 기수 트리와 적응형 기수 트리의 주요 차이점은 자식 요소의 수에 따라 각 노드의 크기가 가변적이며, 새 항목을 추가할 때 크기가 증가한다는 것이다. 따라서 적응형 기수 트리는 속도를 줄이지 않고 공간을 더 효율적으로 사용한다.^[10][11][12]

일반적인 관행은 부모가 데이터 집합에서 유효한 키를 나타내는 상황에서 자식이 하나만 있는 부모를 허용하지 않는 기준을 완화하는 것이다. 이 변형 기수 트리는 적어도 두 개 이상의 자식을 가진 내부 노드만 허용하는 것보다 더 높은 공간 효율성을 달성한다.^[13]

같이 보기

• 접두사 트리 (트라이로도 알려짐)
• 결정론적 비순환 유한 상태 오토마타 (DAFSA)
• 삼항 탐색 트리
• 해시 트라이
• 결정론적 유한 오토마타
• 주디 배열
• 검색 알고리즘
• 확장 가능 해싱
• 해시 배열 매핑 트라이
• 접두사 해시 트리
• 버스트소트
• 룰레오 알고리즘
• 허프먼 부호화