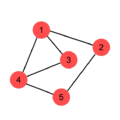
연결 성분  을 갖는 그래프의 선 그래프는 다음과 같다.
을 갖는 그래프의 선 그래프는 다음과 같다.

휘트니 정리(영어: Whitney theorem)에 따르면, 임의의 두 연결 그래프  ,
,  에 대하여, 다음 두 조건이 서로 동치이다.
에 대하여, 다음 두 조건이 서로 동치이다.

 이거나,
이거나,  이거나,
이거나,  . 여기서
. 여기서  은 완전 그래프,
은 완전 그래프,  은 완전 이분 그래프이다.
은 완전 이분 그래프이다.
이는 해슬러 휘트니가 증명하였다.
 선 그래프의 유도 부분 그래프로 존재할 수 없는 9개의 그래프
선 그래프의 유도 부분 그래프로 존재할 수 없는 9개의 그래프
임의의 그래프  에 대하여, 다음 두 조건이 동치이다.[1][2]
에 대하여, 다음 두 조건이 동치이다.[1][2]
 인 그래프
인 그래프  이 존재한다.
이 존재한다. 는 9개의 특별한 그래프들을 유도 부분 그래프로 포함하지 않는다 (그림 참조).
는 9개의 특별한 그래프들을 유도 부분 그래프로 포함하지 않는다 (그림 참조).
선 그래프의 반복
유한 연결 그래프  에 대하여, 다음 두 조건이 동치이다.
에 대하여, 다음 두 조건이 동치이다.

 는 순환 그래프
는 순환 그래프  이다 (
이다 ( ).
).
임의의 유한 연결 그래프  에 대하여, 그래프의 열
에 대하여, 그래프의 열

은 다음 네 가지 가운데 하나의 현상을 보인다.[3]
- 만약
 가 순환 그래프라면 이는 항등열이다.
가 순환 그래프라면 이는 항등열이다.
- 만약
 가 완전 이분 그래프
가 완전 이분 그래프  라면
라면  이다.
이다.
- 만약
 가 경로 그래프
가 경로 그래프  이라면
이라면  이므로 결국 공 그래프
이므로 결국 공 그래프  이 된다.
이 된다.
 가 순환 그래프나 경로 그래프 또는
가 순환 그래프나 경로 그래프 또는  가 아니라면,
가 아니라면,  와
와  는 무한대로 발산한다.
는 무한대로 발산한다.
연결 그래프가 아닌 경우, 각 연결 성분에 위 분류가 적용된다.