반지름이 a 인 원기둥에 기울기 b/a (or pitch 2πb) 인 나선은 아래와 같이 벡터 함수로 나타낼 수 있다.
![{\displaystyle t\mapsto (a\cos t,a\sin t,bt),t\in [0,T]}](//wikimedia.org/api/rest_v1/media/math/render/svg/93d3e0b26d648578d282662c605919e609ab3636)
나선 위에 있는 점의 위치벡터는 아래와 같다.

이를 미분하여 속도와 가속도를 구하면


이다. 속력과 가속도 크기를 구하면 아래와 같다.


호의 길이를 구하는 변수를 구하면

이다. 이제 변수  로 위치벡터를 다시 매개변수화하자.
로 위치벡터를 다시 매개변수화하자.

변수  에 대하여 미분하여 단위 접선벡터를 구하고 이를 다시 미분하여 곡률 벡터를 구하면
에 대하여 미분하여 단위 접선벡터를 구하고 이를 다시 미분하여 곡률 벡터를 구하면


이다. 따라서 나선의 곡률은  이다.
이다.
단위 법선벡터를 구하면

이므로 이중법선벡터는 아래와 같다.
![{\displaystyle \mathbf {B} =\mathbf {T} \times \mathbf {N} ={\frac {1}{\sqrt {a^{2}+b^{2}}}}{\bigg [}b\sin {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {i} -b\cos {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {j} +a\mathbf {k} {\bigg ]}}](//wikimedia.org/api/rest_v1/media/math/render/svg/4a6f1f86f8adb11b23cae7fbcc4ba4a8e60dd456)
이중법선벡터를 미분하여 비틀림(토션)을 구할 수 있다.
![{\displaystyle {\frac {d\mathbf {B} }{ds}}={\frac {1}{a^{2}+b^{2}}}{\bigg [}b\cos {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {i} +b\sin {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {j} +0\mathbf {k} {\bigg ]}}](//wikimedia.org/api/rest_v1/media/math/render/svg/f0e10826ada5a48b614c5f015e7b0cf436d8fdf9)
비틀림은  이다.
이다.
이처럼 나선은 곡률과 비틀림이 상수인 곡선이다.
참고 공간 곡선 운동에 관하여[2]
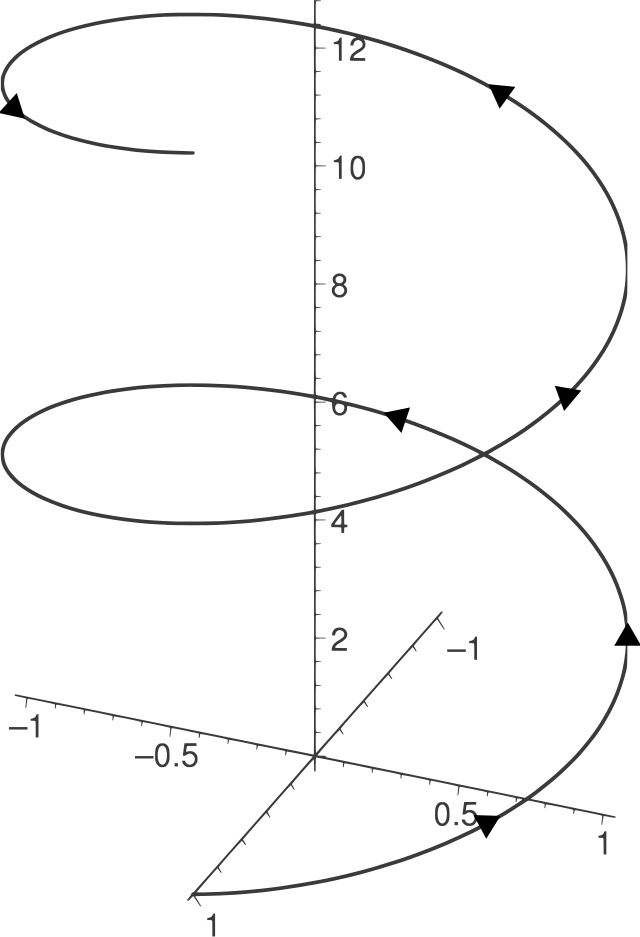




![{\displaystyle t\mapsto (a\cos t,a\sin t,bt),t\in [0,T]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/93d3e0b26d648578d282662c605919e609ab3636)












![{\displaystyle \mathbf {B} =\mathbf {T} \times \mathbf {N} ={\frac {1}{\sqrt {a^{2}+b^{2}}}}{\bigg [}b\sin {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {i} -b\cos {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {j} +a\mathbf {k} {\bigg ]}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/4a6f1f86f8adb11b23cae7fbcc4ba4a8e60dd456)
![{\displaystyle {\frac {d\mathbf {B} }{ds}}={\frac {1}{a^{2}+b^{2}}}{\bigg [}b\cos {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {i} +b\sin {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {j} +0\mathbf {k} {\bigg ]}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/f0e10826ada5a48b614c5f015e7b0cf436d8fdf9)
