상위 질문
타임라인
채팅
관점
모눈종이
위키백과, 무료 백과사전
Remove ads
모눈종이(영어: Graph paper, coordinate paper, grid paper, squared paper)는 가는 선으로 정규 격자를 이루도록 인쇄된 종이이다. 낱장으로 사용하거나 공책 또는 그래프 책에 묶인 형태로 구할 수 있다.
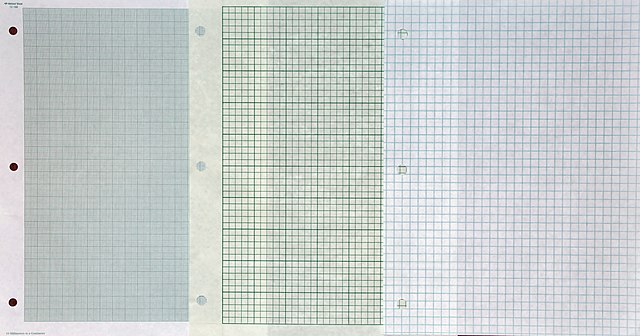
모눈종이는 일반적으로 수학 및 공학 교육 환경, 연습장 및 연구노트에서 발견된다. 그리고 수학 기호, 함수나 실험 데이터, 또는 곡선을 그리는 데 사용된다.
역사
메트로폴리탄 미술관이 소유한 약 1596년경 작성된 책은 각 페이지에 목판 인쇄로 인쇄된 격자가 있다. 소유자는 이 격자를 사용하여 흑백 및 컬러로 일종의 픽셀아트를 만들었다.[1]
일반적으로 영국 출신의 닥터 벅스턴(Dr. Buxton)이 최초로 모눈종이(coordinate paper)를 상업적으로 출판했다고 본다. 그는 1794년에 직사각형 좌표 격자가 인쇄된 종이에 특허를 받았다.[2] 한 세기 후, 시카고 대학교의 저명한 수학자 E. H. 무어(E. H. Moore)는 고등학생과 대학생들이 '눈금선'이 있는 종이나 연습장을 사용할 것을 권장했다.[3] H. S. 홀(H. S. Hall)과 S. R. 나이트(S. R. Knight)의 1906년판 《초급 대수학》(Algebra for Beginners)에는 "눈금 용지는 좋은 품질이어야 하며 인치 및 10분의 1인치 단위로 정확하게 선이 그어져 있어야 한다. 경험상으로 '밀리미터' 용지처럼 더 작은 단위는 초보자의 손에는 사실상 가치가 없다"는 단호한 언급이 포함되어 있다.[4]
영문 표기에 대해서, '그래프 용지(graph paper)'라는 용어는 미국에서 빠르게 퍼지지 않았다. H. S. 홀과 F. H. 스티븐스(F. H. Stevens)의 1919년작 《학교 산수》(A School Arithmetic)에는 '격자 용지(squared paper)'를 사용한 그래프에 대한 장이 있었다. W. A. 윌슨(W. A. Wilson)과 J. A. 트레이시(J. A. Tracey)의 1937년작 《해석 기하학》(Analytic Geometry)에서는 '좌표 용지(coordinate paper)'라는 문구를 사용했다. '격자 용지(squared paper)'라는 용어는 영국에서 더 오래 사용되었는데, 예를 들어 W. M. 베이커(W. M. Baker)와 A. A. 본(A. A. Bourne)이 런던에서 출판한 2023년판 《공립 학교 산수》(Public School Arithmetic)에서 사용되었다.[4]
Remove ads
형식
요약
관점
- 쿼드 용지(Quad paper) 또는 쿼드릴 용지(quadrille paper)라고도 불리는데, 이는 큰 사각형이란 뜻의 프랑스어 'quadrillé'에서 유래했다.[5] 연한 파란색이나 회색으로 인쇄된 격자가 종이 가장자리까지 있는 일반적인 형태의 모눈종이다. 미국과 캐나다에서는 크게 세부적이지 않은 작업을 위해 인치 당 2칸, 4칸 또는 5칸이 있는 경우가 많다. 유럽에서는 보통 5 밀리미터 x 5 밀리미터 칸이 수학 연습장과 연구노트에 사용된다.
- 점 종이는 격자선 대신 교차점에 점을 사용한다. 불렛 저널에 자주 사용된다.
- 공학 용지 또는 공학 도면은[6] 전통적으로 연한 녹색 또는 황갈색의 반투명 종이에 인쇄되고, 인치 당 4, 5 또는 10칸이 있을 수 있다. 격자선은 각 페이지 뒷면에 인쇄되어 앞면에 희미하게 비친다. 각 페이지에는 인쇄되지 않은 여백이 있다. 복사하거나 스캔할 때 격자선은 일반적으로 결과물에 나타나지 않아 결과물이 깔끔하고 정돈된 모습으로 보인다. 미국과 캐나다에서는 일부 공학 교수들은 학생들이 숙제를 공학 용지에 작성하도록 한다.[6][7]
- 밀리미터 용지는 센티미터당 10칸이며 제도에 사용된다.
- 육각형 용지는 사각형 대신 정육각형을 보여준다. 이는 기하학적 타일링 또는 테셀레이션 디자인을 그리는 등 다양한 용도로 사용될 수 있다.
- 등측 투영 용지 또는 3D 모눈종이는 작은 삼각형으로 이루어진 60° 격자로 된 세 줄의 안내선을 사용하는 삼각형 모눈종이이다. 삼각형은 여섯 개씩 묶여 육각형을 이룬다. 이름에서 알 수 있듯이 등축 투영도 또는 3차원처럼 보이도록 그리는 데 사용된다. 다른 기능 외에도 삼각 자수 디자인에 사용될 수 있다. 각도를 정확하게 그리는 데 사용할 수 있다.
- 로그 용지는 로그 눈금에 해당하는 다양한 너비의 사각형이 그려져 있어 반대수 그래프 또는 양대수 그래프에 사용된다.
- 정규 확률 용지는 다양한 너비의 사각형이 있는 또 다른 모눈종이다. 정규 분포 함수의 그래프가 직선으로 표시되도록 설계되었으며, 즉 정규 확률을 매핑할 때 사용될 수 있다.[8]
- 극좌표 용지는 동심원이 작은 호 또는 '파이 조각'으로 나뉘어 있어 극좌표에서 그래프를 그릴 수 있다.
- 삼원 (삼각형) 모눈종이는 정삼각형으로 되어 있으며, 각 변이 보통 10개 이상 나눠진 작은 정삼각형으로 나뉘어 있다. 이는 세 가지 구성 요소 또는 세 가지 차원이 있는 시스템에서 구성 백분율을 매핑하는 데 사용된다. (삼원도 참조)
일반적으로 격자를 표시하는 그래프는 사각형을 데카르트 좌표계에 측정값을 표시하는 데 사용할 수 있기 때문에 데카르트 그래프라고도 불린다.
Remove ads
예시
- 일반 모눈종이
- 양대수 모눈종이
- 반대수 모눈종이
- 정규 확률 용지
- 등각 투영 용지
- 극좌표 용지
- 공학 용지
- 삼원 모눈종이
- 두 가지 스타일의 낱장 모눈종이
같이 보기
- 괘지
- 시험지
각주
외부 링크
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads











