밀도 반전

물리학, 특히 통계역학에서 밀도 반전(population inversion) 또는 반전 분포는 원자나 분자의 집합과 같은 열역학계가 하위의 비여기 에너지 준위보다 상위의 들뜬 상태에 더 많은 구성원이 존재하는 상태에 있을 때 발생한다. 이는 열평형 상태에 있는 많은 익숙하고 흔히 접하는 물리계에서는 불가능하므로 "반전"이라고 불린다. 이 개념은 표준 레이저의 작동에 밀도 반전 생성이 필수적인 단계이기 때문에 레이저 물리학에서 근본적으로 중요하다.

조건

밀도 반전의 개념을 이해하려면 일부 열역학과 빛이 물질과 상호 작용하는 방식을 이해해야 한다. 이를 위해 활성 레이저 매질을 형성하는 매우 간단한 원자 집합을 고려하는 것이 유용하다.

N개의 원자 그룹이 있다고 가정해 보자. 각 원자는 다음 두 가지 에너지 준위 중 하나에 있을 수 있다.

1. 에너지 E₁을 갖는 바닥 상태 또는
2. 에너지 E₂를 갖는 들뜬 상태 (E₂ > E₁)

바닥 상태에 있는 원자의 수는 N₁로 주어지고, 들뜬 상태에 있는 원자의 수는 N₂로 주어진다. 총 N개의 원자가 있으므로,

${\displaystyle N_{1}+N_{2}=N}$

두 상태 사이의 에너지 차이는 다음과 같이 주어진다.

${\displaystyle \Delta E_{12}=E_{2}-E_{1},}$

이는 원자와 상호 작용하는 빛의 특성 진동수 ${\textstyle \nu _{12}}$를 결정한다. 이는 다음 관계에 의해 주어진다.

${\displaystyle E_{2}-E_{1}=\Delta E_{12}=h\nu _{12},}$

여기서 h는 플랑크 상수이다.

만약 원자 그룹이 열평형 상태에 있다면, 맥스웰-볼츠만 통계로부터 각 상태에 있는 원자 수의 비율이 두 볼츠만 분포의 비율, 즉 볼츠만 인자로 주어진다는 것을 알 수 있다.

${\displaystyle {\frac {N_{2}}{N_{1}}}={\frac {g_{2}}{g_{1}}}\exp {\frac {-(E_{2}-E_{1})}{kT}},}$

여기서 T는 원자 그룹의 열역학 온도, k는 볼츠만 상수, g₁과 g₂는 각 상태의 축퇴 에너지 수준이다.

실온 (T ≈ 300 K)에서 가시광선 주파수 (ν ≈ 5×10¹⁴ Hz)에 해당하는 빛의 에너지 차이 ΔE에 대한 두 상태의 개체수 비율을 계산할 수 있다. 이 경우 ΔE = E₂ − E₁ ≈ 2.07 eV이고, kT ≈ 0.026 eV이다. E₂ − E₁ ≫ kT이므로, 위 방정식에서 지수의 인수는 큰 음수이며, 따라서 N₂/N₁은 매우 작아진다. 즉, 들뜬 상태에는 거의 원자가 없다. 열평형 상태에서는 낮은 에너지 상태가 높은 에너지 상태보다 더 많이 채워져 있으며, 이것이 시스템의 정상 상태이다. T가 증가함에 따라 고에너지 상태의 전자 수(N₂)는 증가하지만, 열평형 상태의 시스템에서는 N₂가 N₁을 초과하지 않는다. 오히려 무한 온도에서는 N₂와 N₁의 개체수가 같아진다. 다시 말해, 열평형 상태의 시스템에서는 밀도 반전(N₂/N₁ > 1)이 결코 존재할 수 없다. 따라서 밀도 반전을 달성하려면 시스템을 비평형 상태로 밀어 넣어야 한다.

빛과 물질의 상호 작용

원자 시스템과 빛 사이에는 세 가지 유형의 상호 작용이 있다.

흡수

 이 부분의 본문은 흡수 (광학)입니다.

만약 진동수 ν₁₂의 빛 (광자)이 원자 그룹을 통과하면, 바닥 상태에 있는 전자에 의해 빛이 흡수되어 전자가 더 높은 에너지 상태로 들뜨게 될 가능성이 있다. 흡수율은 빛의 복사 밀도에 비례하며, 또한 현재 바닥 상태에 있는 원자의 수 N₁에 비례한다.

자연 방출

 이 부분의 본문은 자연 방출입니다.

원자가 들뜬 상태에 있다면, 들뜬 상태에 있는 원자의 수 N₂에 비례하는 속도로 바닥 상태로의 자발적인 붕괴 현상이 일어날 것이다. 두 상태 사이의 에너지 차이 ΔE₂₁는 위에서 설명한 진동수-에너지 관계에 따라 진동수 ν₂₁의 광자로 원자에서 방출된다.

광자는 추계학적으로 방출되며, 들뜬 원자 그룹에서 방출되는 광자들 사이에는 고정된 위상 관계가 없다. 다시 말해, 자연 방출은 비결맞음이다. 다른 과정이 없을 때, 시간 t에서의 들뜬 상태 원자 수는 다음과 같이 주어진다.

${\displaystyle N_{2}(t)=N_{2}(0)\exp {\frac {-t}{\tau _{21}}},}$

여기서 N₂(0)는 시간 t = 0에서의 들뜬 원자 수이며, τ₂₁는 두 상태 사이의 전이의 평균 수명이다.

유도 방출

 이 부분의 본문은 유도 방출입니다.

원자가 이미 들뜬 상태에 있다면, 들뜬 상태에서 바닥 상태로의 전이 에너지 차이 ΔE에 해당하는 진동수 ν₂₁를 가진 광자가 통과하면서 자극을 받을 수 있다. 이 경우, 들뜬 원자는 바닥 상태로 이완하고, 두 번째 진동수 ν₂₁를 가진 광자를 생성한다. 원래 광자는 원자에 흡수되지 않으므로, 결과적으로 동일한 진동수를 가진 두 개의 광자가 발생한다. 이 과정을 유도 방출이라고 한다.

구체적으로, 들뜬 원자는 외부 전계에 의해 진동하는 작은 전기 쌍극자처럼 행동한다. 이 진동의 결과 중 하나는 전자가 가장 낮은 에너지 상태로 붕괴되도록 유도한다는 것이다. 광자의 전자기장 존재로 인해 이러한 일이 발생하면, "자극하는" 광자와 동일한 위상과 방향으로 광자가 방출되며, 이를 유도 방출이라고 한다.

유도 방출이 발생하는 속도는 들뜬 상태에 있는 원자의 수 N₂와 빛의 복사 밀도에 비례한다. 단일 들뜬 원자에서 광자가 유도 방출을 유발할 기본 확률은 알베르트 아인슈타인에 의해 바닥 상태에 있는 원자에 의해 광자가 흡수될 확률과 정확히 같다는 것이 밝혀졌다. 따라서 바닥 상태와 들뜬 상태의 원자 수가 같을 때, 유도 방출 속도는 주어진 복사 밀도에 대한 흡수 속도와 같다.

유도 방출의 핵심적인 특징은 유도된 광자가 입사 광자와 동일한 진동수와 위상을 가진다는 것이다. 다시 말해, 두 광자는 결맞음이다. 광 증폭과 레이저 시스템의 생산을 가능하게 하는 것이 바로 이 속성이다. 레이저 작동 중에는 위에서 설명한 세 가지 빛-물질 상호 작용이 모두 발생한다. 처음에는 아래에서 설명할 펌핑이라는 과정을 통해 원자가 바닥 상태에서 들뜬 상태로 에너지를 받는다. 이 원자 중 일부는 자연 방출을 통해 붕괴하여 진동수 ν의 광자 형태의 비결맞음 빛을 방출한다. 이 광자들은 일반적으로 광공진기를 통해 레이저 매질로 다시 공급된다. 이 광자 중 일부는 바닥 상태의 원자에 흡수되어 레이저 과정에서 손실된다. 그러나 일부 광자는 들뜬 상태의 원자에서 유도 방출을 일으켜 또 다른 결맞음 광자를 방출한다. 사실상 이는 광 증폭을 초래한다.

단위 시간당 증폭되는 광자의 수가 흡수되는 광자의 수보다 많으면, 그 결과는 지속적으로 증가하는 광자 수가 생성되는 것이다. 이때 레이저 매질은 단위보다 큰 이득을 가진다고 말한다.

위에서 흡수와 유도 방출에 대한 설명에서, 이 두 과정의 속도가 각각 바닥 상태와 들뜬 상태의 원자 수 N₁과 N₂에 비례한다는 것을 상기하자. 만약 바닥 상태가 들뜬 상태보다 더 많은 개체수를 가지고 있다면 (N₁ > N₂), 흡수 과정이 지배적이어서 광자의 순 감쇠가 발생한다. 만약 두 상태의 개체수가 같다면 (N₁ = N₂), 빛의 흡수 속도가 방출 속도와 정확히 균형을 이룬다. 이때 매질은 광학적으로 투명하다고 말한다.

만약 높은 에너지 상태가 낮은 에너지 상태보다 더 많은 개체수를 가진다면 (N₁ < N₂), 방출 과정이 지배적이며 시스템 내의 빛은 순 강도 증가를 겪는다. 따라서 흡수보다 더 빠른 유도 방출 속도를 생성하려면 두 상태의 개체수 비율이 다음을 만족해야 한다는 것이 분명하다. N₂/N₁ > 1; 다시 말해, 레이저 작동을 위해서는 밀도 반전이 필요하다.

선택규칙

 이 부분의 본문은 선택규칙입니다.

전자기 복사를 포함하는 많은 전이들은 양자 역학에 의해 엄격히 금지된다. 허용되는 전이들은 복사 전이가 허용되는 조건을 설명하는 소위 선택규칙에 의해 설명된다. 예를 들어, 전이들은 시스템의 총 스핀 각운동량인 ΔS = 0인 경우에만 허용된다. 실제 재료에서는 결정 격자와의 상호 작용과 같은 다른 효과들이 대체 메커니즘을 제공하여 형식적인 규칙을 우회한다. 이러한 시스템에서는 금지된 전이가 발생할 수 있지만, 일반적으로 허용된 전이보다 느린 속도로 발생한다. 고전적인 예로는 S = 0인 바닥 상태, S = 0인 들뜬 상태, S = 1인 중간 상태를 갖는 재료의 인광이 있다. 중간 상태에서 빛 방출에 의한 바닥 상태로의 전이는 선택 규칙 때문에 느리다. 따라서 외부 조명이 제거된 후에도 방출이 계속될 수 있다. 대조적으로 재료의 형광은 외부 조명이 제거되면 방출이 멈추는 특징이 있다.

복사의 흡수 또는 방출을 포함하지 않는 전이들은 선택 규칙의 영향을 받지 않는다. 들뜬 S = 0 및 S = 1 상태와 같은 준위 간의 비복사 전이는 S = 0 개체수 중 일부가 자발적으로 바닥 상태로 돌아가기 전에 충분히 빠르게 진행될 수 있다.

재료에 중간 상태가 존재한다는 것은 레이저의 광학 펌핑 기술에 필수적이다 (아래 참조).

생성

레이저 작동을 위해서는 밀도 반전이 필요하지만, 열평형 상태에 있는 위에서 설명한 이론적인 두 에너지 준위 원자 그룹에서는 달성할 수 없다. 사실, 원자를 바닥 상태에서 들뜬 상태로 직접적이고 지속적으로 여기시키는 어떤 방법 (예: 광학 흡수)이라도 결국 자발 및 유도 방출이라는 역여기 과정과 평형에 도달할 것이다. 최선으로 두 상태의 동일한 개체수, N₁ = N₂ = N/2를 달성할 수 있으며, 이는 광학 투명성을 초래하지만 순 광학 이득은 없다. 지속적인 비평형 조건을 달성하려면 들뜬 상태를 채우는 간접적인 방법을 사용해야 한다.

레이저에서

3준위 레이저에서

3준위 레이저 에너지 다이어그램.

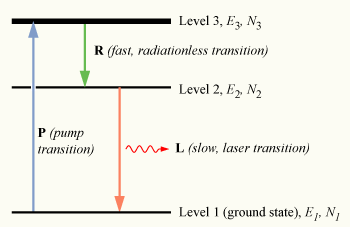
3준위 레이저는 밀도 반전을 달성할 수 있다. 이것은 N개의 원자 그룹으로 구성되며, 각 원자는 에너지 E₁, E₂, E₃를 갖는 세 가지 에너지 상태, 즉 준위 1, 2, 3 중 하나에 존재할 수 있고, 각각 N₁, N₂, N₃의 개체수를 갖는다. E₁ < E₂ < E₃이다. 즉, 준위 2의 에너지는 준위 1과 준위 3의 에너지 사이에 있다. 준위 1은 또한 바닥 상태라고도 불린다.

초기에 원자 시스템은 열평형 상태에 있으며, 대부분의 원자는 바닥 상태에 있다. 즉, N₁ ≈ N, N₂ ≈ N₃ ≈ 0이다. 원자는 준위 1에서 준위 3으로 여기될 수 있으며, 이 행위를 펌핑이라고 한다. 원자가 진동수 ${\displaystyle \scriptstyle \nu _{13}\,=\,{\frac {1}{h}}\left(E_{3}-E_{1}\right)}$의 빛에 노출될 때 발생할 수 있으며, 광학 흡수 과정은 전자를 준위 1에서 준위 3으로 여기시킨다. 직접적으로 빛 흡수를 포함하지 않는 방법도 있다. 예를 들어 전기 방전이나 화학 반응이 있다. 준위 3은 때때로 펌프 준위 또는 펌프 띠라고 불리며, 에너지 전이 E₁ → E₃는 펌프 전이(오른쪽 그림에서 P로 표시된 전이)라고 불린다.

매체를 펌핑하면 상당수의 원자가 준위 3으로 전이하여 N₃ > 0이 된다. 레이저 작동에 적합한 매체를 갖기 위해서는 이 들뜬 원자들이 빠르게 준위 2로 붕괴되어야 한다. 이 전이에서 방출되는 에너지는 광자(자연 방출)로 방출될 수 있다. 그러나 실제로는 3 → 2 전이는 일반적으로 비복사성(도표에서 R로 표시된 전이)이며, 광자 생성 없이 에너지가 원자를 둘러싼 호스트 물질의 진동 운동(열)으로 전달된다. 이 현상을 오제 효과라고 한다.

준위 2의 전자는 자연 방출을 통해 준위 1로 붕괴될 수 있으며, 진동수 ν₁₂의 광자(주어진 E₂ − E₁ = hν₁₂)를 방출하는데, 이를 레이저 전이(도표에서 L로 표시된 전이)라고 한다. 이 전이의 수명 τ₂₁이 비복사성 3 → 2 전이 τ₃₂의 수명보다 훨씬 길다면(만약 τ₂₁ ≫ τ₃₂, 즉 유리한 수명 비율로 알려진 경우), E₃의 개체수는 본질적으로 0이 되고(N₃ ≈ 0), 들뜬 상태 원자의 개체수가 준위 2에 축적될 것이다(N₂ > 0). 만약 N개의 원자 중 절반 이상이 이 상태에 축적될 수 있다면, 이는 바닥 상태 N₁의 개체수를 초과할 것이다. 따라서 준위 1과 2 사이에 밀도 반전(N₂ > N₁)이 달성되었으며, 진동수 ν₂₁에서 광 증폭을 얻을 수 있다.

밀도 반전을 얻으려면 원자의 절반 이상을 바닥 상태에서 들뜬 상태로 여기시켜야 하므로 레이저 매질을 매우 강하게 펌핑해야 한다. 이 때문에 3준위 레이저는 발견된 최초의 레이저 유형임에도 불구하고 (1960년 시어도어 마이먼이 루비 레이저 매질을 기반으로 발견), 비효율적이다. 3준위 시스템은 또한 준위 3과 2 사이에 복사 전이가 있고 준위 2와 1 사이에 비복사 전이가 있을 수 있다. 이 경우 펌핑 요구 사항이 약해진다. 실제로 대부분의 레이저는 아래에서 설명하는 4준위 레이저이다.

4준위 레이저에서

4준위 레이저 에너지 다이어그램.

4준위 레이저에는 에너지 E₁, E₂, E₃, E₄를 가지는 네 개의 에너지 준위(준위 1, 2, 3, 4)와 각각 N₁, N₂, N₃, N₄의 개체수가 존재한다. 각 준위의 에너지는 E₁ < E₂ < E₃ < E₄를 만족한다.

이 시스템에서 펌핑 전이 P는 원자를 준위 1에서 준위 4(펌프 준위)로 여기시킨다. 준위 4에서 원자는 빠른 비복사 전이 Ra를 통해 준위 3으로 붕괴한다. 레이저 전이 L의 수명이 Ra의 수명보다 길기 때문에(τ₃₂ ≫ τ₄₃), 준위 3(상위 레이저 준위)에 개체수가 축적되며, 이는 자발 방출 또는 유도 방출을 통해 준위 2(하위 레이저 준위)로 이완될 수 있다. 이 준위 또한 준위 1로 빠른 비복사 붕괴 Rb를 가진다.

3준위 레이저와 마찬가지로 빠른 비복사성 붕괴 전이의 존재로 인해 펌프 띠의 개체수가 빠르게 고갈된다(N₄ ≈ 0). 4준위 시스템에서는 준위 2(하위 레이저 준위)에 있는 모든 원자도 빠르게 탈여기되어 해당 상태의 개체수가 무시할 만하게 된다(N₂ ≈ 0). 이는 준위 3(상위 레이저 준위)에 상당한 개체수가 축적될 경우 준위 2에 대해 밀도 반전을 형성하기 때문에 중요하다. 즉, N₃ > 0인 한, N₃ > N₂가 되므로 밀도 반전이 달성된다. 따라서 광학 증폭 및 레이저 작동은 주파수 ν₃₂ (E₃ − E₂ = hν₃₂)에서 발생할 수 있다.

상위 레이저 준위로 몇 개의 원자만 여기되어도 밀도 반전이 형성될 수 있으므로^[왜?], 4준위 레이저는 3준위 레이저보다 훨씬 효율적이며, 대부분의 실용적인 레이저는 이 유형이다. 실제로는 레이저 과정에 4개보다 훨씬 많은 에너지 준위가 관여할 수 있으며, 이러한 준위들 사이에서 복잡한 여기 및 이완 과정이 발생한다. 특히, 펌프 띠는 여러 개의 별개의 에너지 준위 또는 연속적인 준위로 구성될 수 있으며, 이는 넓은 파장 범위에 걸쳐 매질의 광학 펌핑을 가능하게 한다.

특성

3준위 및 4준위 레이저 모두에서 펌핑 전이의 에너지가 레이저 전이의 에너지보다 크다는 점에 유의한다. 이는 레이저가 광학적으로 펌핑되는 경우 펌핑 빛의 진동수가 결과적인 레이저 빛의 진동수보다 커야 함을 의미한다. 다시 말해, 펌프 파장은 레이저 파장보다 짧다. 일부 매질에서는 여러 낮은 에너지 전이 간의 다중 광자 흡수를 사용하여 펌프 준위에 도달하는 것이 가능하며, 이러한 레이저를 업컨버전 레이저라고 한다.

많은 레이저에서 레이저 과정은 위 모델에서 설명된 바와 같이 원자들 간의 서로 다른 전자 에너지 상태 전이를 포함하지만, 이것이 레이저 작동을 유발할 수 있는 유일한 메커니즘은 아니다. 예를 들어, 레이저 매질이 완전한 분자로 구성되고 에너지 상태가 분자의 진동 및 회전 모드에 해당하는 많은 일반적인 레이저(색소 레이저, 이산화탄소 레이저 등)가 있다. 이는 물 메이저, 자연에서 발생하는 경우와 같다.

일부 매질에서는 추가적인 광학 또는 마이크로파 장을 가함으로써 양자 결맞음 효과를 사용하여 바닥 상태에서 들뜬 상태로의 전이 가능성을 줄일 수 있다. 밀도 반전 없는 레이저로 알려진 이 기술은 두 상태 간에 밀도 반전을 생성하지 않고도 광 증폭을 가능하게 한다.

메이저에서

유도 방출은 전자기 스펙트럼의 마이크로파 영역에서 처음 관찰되었으며, 마이크로파 복사 유도 방출 증폭(Microwave Amplification by Stimulated Emission of Radiation)의 약어로 MASER가 탄생했다. 마이크로파 영역에서는 에너지 상태 사이의 분자 볼츠만 분포가 실온에서 모든 상태가 거의 동일하게 채워진다.

이러한 조건에서 밀도 반전을 생성하려면 특성 차이에 따라 시스템에서 일부 원자나 분자를 선택적으로 제거해야 한다. 예를 들어, 수소 메이저에서는 외로운 전자가 핵 스핀과 평행한 스핀 상태에서 반평행한 스핀 상태로 뒤집히는 원자 수소의 잘 알려진 21cm 파동 전이를 사용하여 밀도 반전을 생성할 수 있다. 이는 평행 상태가 자기 모멘트를 가지고 있고 반평행 상태는 그렇지 않기 때문이다. 강한 불균일 자기장은 혼합 상태 원자 빔에서 고에너지 상태의 원자를 분리할 것이다. 분리된 개체수는 유도 방출을 나타낼 수 있는 밀도 반전을 나타낸다.

같이 보기

• 레이저 구조
• 음의 온도
• 양자 전자공학

각주

• Svelto, Orazio (1998). Principles of Lasers, 4th ed. (trans. David Hanna), Springer. ISBN 0-306-45748-2