볼록 집합

기하학에서 볼록 집합(영어: convex set)은 임의의 두 점을 잇는 선분을 포함하는, 유클리드 공간의 부분 집합이다.

볼록 집합

볼록 집합이 아닌 집합

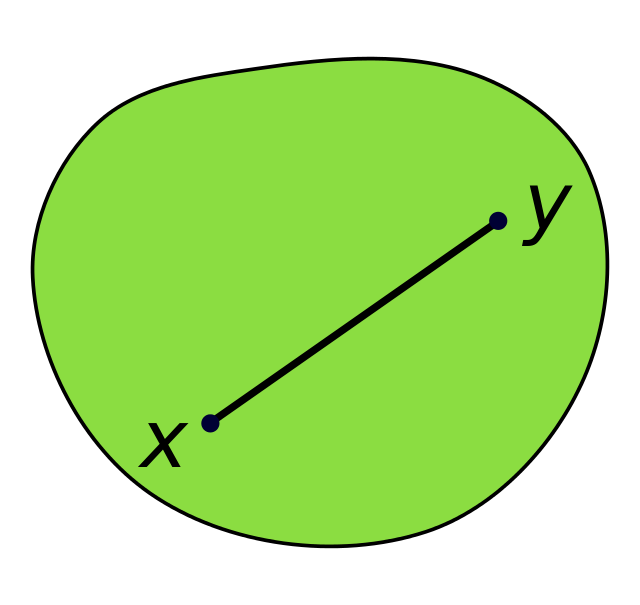
정의

${\displaystyle K\in \{\mathbb {R} ,\mathbb {C} \}}$가 실수체 또는 복소수체라고 하자. ${\displaystyle K}$-위상 벡터 공간 ${\displaystyle V}$의 부분 집합 ${\displaystyle S\subseteq V}$가 다음 조건을 만족시키면, 볼록 집합이라고 한다.

• 임의의 ${\displaystyle u,v\in S}$ 및 ${\displaystyle t\in [0,1]}$에 대하여, ${\displaystyle (1-t)u+tv\in S}$

국소 볼록 집합(영어: locally convex set)은 임의의 점이 (그 부분 집합에서의) 볼록 근방을 갖는 부분 집합이다.

다각 연결 집합

실수 위상 벡터 공간 ${\displaystyle V}$의 부분 집합 ${\displaystyle S\subseteq V}$가 다음 조건을 만족시키면, 다각 연결 집합(영어: polygonally connected set)이라고 한다.

• 임의의 ${\displaystyle u,v\in S}$에 대하여, 다음 세 조건을 만족시키는 자연수 ${\displaystyle n\in \mathbb {N} }$ 및 ${\displaystyle u_{0},u_{1},u_{2},\dotsc ,u_{n}\in S}$가 존재한다.
  • ${\displaystyle u_{0}=u}$
  • ${\displaystyle u_{n}=v}$
  • 각 ${\displaystyle i\in \{1,2,\dots ,n\}}$ 및 임의의 ${\displaystyle t\in [0,1]}$에 대하여, ${\displaystyle (1-t)u_{i-1}+tu_{i}\in S}$

위 정의에서 ${\displaystyle n}$을 어떤 자연수로 고정하면, ${\displaystyle n}$-다각 연결 집합(영어: ${\displaystyle n}$-polygonally connected set)의 정의를 얻는다. 이 경우, 볼록 집합은 1-다각 연결 집합과 동치이다.

성질

연산에 대한 닫힘

볼록 집합들의 교집합은 볼록 집합이다. 볼록 집합들의 상향 집합의 합집합은 볼록 집합이다. (더 일반적인 결과는 성립하지 않는다. 예를 들어, 서로 만나는 두 직선의 합집합은 볼록 집합이 아니다.) 볼록 집합의 폐포·내부는 볼록 집합이다.

함의 관계

모든 다각 연결 집합은 경로 연결 공간이다. 모든 ${\displaystyle n}$-다각 연결 집합은 다각 연결 집합이다. (그러나 다각 연결 집합은 어떤 ${\displaystyle n}$에 대하여 ${\displaystyle n}$-다각 연결 집합일 필요가 없다.) 모든 별모양 집합은 2-다각 연결 집합이다. 모든 (공집합이 아닌) 볼록 집합은 별모양 집합이다.

실수 노름 공간의 연결 열린집합은 항상 다각 연결 집합이다.^{[1]:81, Exercise 3.4.2}

유클리드 공간 ${\displaystyle \mathbb {R} ^{n}}$의 부분 집합 ${\displaystyle S\subseteq \mathbb {R} ^{n}}$에 대하여, 만약 ${\displaystyle S}$가 닫힌집합이며, 연결 공간이며, 국소 볼록 집합이라면, ${\displaystyle S}$는 볼록 집합이다 (티체-나카지마 정리, 영어: Tietze–Nakajima theorem).^[2]:1306 보다 일반적으로, 만약 ${\displaystyle S}$가 닫힌집합이며, 연결 집합이며, ${\displaystyle n}$개 이하의 국소 비볼록점을 갖는다면, ${\displaystyle S}$는 ${\displaystyle (n+1)}$-다각 연결 집합이다.^{[2]:1305, Theorem 1} 보다 일반적으로, 만약 ${\displaystyle S}$가 닫힌집합이며, 연결 집합이며, ${\displaystyle S}$의 국소 비볼록점의 집합이 (서로소일 필요가 없는) ${\displaystyle n}$개의 볼록 집합의 합집합이라면, ${\displaystyle S}$는 ${\displaystyle (2n+1)}$-다각 연결 집합이다.^{[2]:1305, Theorem 2}

부분 집합의 극대 볼록 집합

실수 위상 벡터 공간 ${\displaystyle V}$의 부분 집합 ${\displaystyle S\subseteq V}$가 주어졌다고 하자. ${\displaystyle S}$의 볼록 집합들은 포함 관계에 따라 부분 순서 집합을 이룬다. 그 극대 원소를 ${\displaystyle S}$의 볼록 성분(영어: convex component)이라고 한다. ${\displaystyle S}$의 임의의 볼록 집합은 ${\displaystyle S}$의 볼록 성분에 포함되며, 임의의 볼록 성분은 연결 집합이므로, ${\displaystyle S}$의 유일한 연결 성분에 포함된다. 그러나 연결 성분과 달리, 볼록 성분들은 서로소일 필요가 없다. 다시 말해, ${\displaystyle S}$의 주어진 볼록 집합을 포함하는 극대 볼록 집합은 유일하지 않을 수 있다.

만약 ${\displaystyle S}$가 닫힌집합이라면, 모든 볼록 성분 역시 닫힌집합이다.

실수 위상 벡터 공간 ${\displaystyle V}$의 부분 집합 ${\displaystyle S\subseteq V}$가 가산 개의 ${\displaystyle S}$의 서로소 볼록 닫힌집합 ${\displaystyle S_{i}}$들의 합집합이라면, ${\displaystyle S}$의 볼록 성분들은 정확히 ${\displaystyle S_{i}}$들이며, 특히 ${\displaystyle S}$의 볼록 성분들은 ${\displaystyle S}$의 분할을 이룬다.^{[3]:Theorem 2.10}

예

실수선 ${\displaystyle \mathbb {R} }$의 볼록 집합은 단순히 구간이다.

집합

${\displaystyle \{(x,x^{2})\colon x\in \mathbb {R} \}}$

은 경로 연결 공간이지만, ${\displaystyle \mathbb {R} ^{2}}$의 다각 연결 집합이 아니다.

역사

티체-나카지마 정리는 하인리히 프란츠 프리드리히 티체(독일어: Heinrich Franz Friedrich Tietze, 1880~1964)^[4]와 나카지마(영어: S. Nakajima)^[5]가 모두 1928년 논문에서 독립적으로 증명하였다.

같이 보기

• 크레인-밀만 정리
• 볼록 폐포