슐츠 방법

슐츠 방법(Schulze method)은 1997년 마커스 슐츠가 개발한 선거 제도이다. 이 방법으로 승자들의 정렬된 목록을 만들어낼 수 있다.

예시

후보자가 5명(A, B, C, D, E)이고 투표자가 45명인 예시를 살펴보자.

선호순서	투표자수
ACBED	5
ADECB	5
BEDAC	8
CABED	3
CAEBD	7
CBADE	2
DCEBA	7
EBADC	8
계	45

짝 대결 행렬

	d[*,A]	d[*,B]	d[*,C]	d[*,D]	d[*,E]
d[A,*]		20	26	30	22
d[B,*]	25		16	33	18
d[C,*]	19	29		17	24
d[D,*]	15	12	28		14
d[E,*]	23	27	21	31

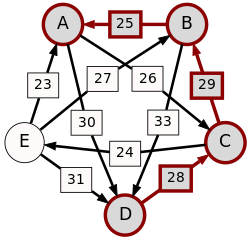
짝 대결 그래프

경로의 강도(strength)는 가장 약한 고리(=노드)의 강도를 말한다. 다음 표는 후보자 각 쌍에 대해 한 후보자 X에서 다른 후보자 Y로 가는 최강 경로를 보여준다. 이들 최강경로에서 가장 약한 고리는 밑줄로 표시되어 있다.

최강경로

	→ A	→ B	→ C	→ D	→ E
A →		A-(30)-D-(28)-C-(29)-B	A-(30)-D-(28)-C	A-(30)-D	A-(30)-D-(28)-C-(24)-E
B →	B-(25)-A		B-(33)-D-(28)-C	B-(33)-D	B-(33)-D-(28)-C-(24)-E
C →	C-(29)-B-(25)-A	C-(29)-B		C-(29)-B-(33)-D	C-(24)-E
D →	D-(28)-C-(29)-B-(25)-A	D-(28)-C-(29)-B	D-(28)-C		D-(28)-C-(24)-E
E →	E-(31)-D-(28)-C-(29)-B-(25)-A	E-(31)-D-(28)-C-(29)-B	E-(31)-D-(28)-C	E-(31)-D

최강경로의 강도

	p[*,A]	p[*,B]	p[*,C]	p[*,D]	p[*,E]
p[A,*]		28	28	30	24
p[B,*]	25		28	33	24
p[C,*]	25	29		29	24
p[D,*]	25	28	28		24
p[E,*]	25	28	28	31

E 후보자는, 모든 다른 후보자 X에 대하여 p[E,X] ≥ p[X,E]이므로 잠재적 승자이다.

• 25 = p[E,A] > p[A,E] = 24이므로 후보자 E는 후보자 A보다 선호된다.
• 28 = p[E,B] > p[B,E] = 24이므로 후보자 E는 후보자 B보다 선호된다.
• 28 = p[E,C] > p[C,E] = 24이므로 후보자 E는 후보자 C보다 선호된다.
• 31 = p[E,D] > p[D,E] = 24이므로 후보자 E는 후보자 D보다 선호된다.
• 28 = p[A,B] > p[B,A] = 25이므로 후보자 A는 후보자 B보다 선호된다.
• 28 = p[A,C] > p[C,A] = 25이므로 후보자 A는 후보자 C보다 선호된다.
• 30 = p[A,D] > p[D,A] = 25이므로 후보자 A는 후보자 D보다 선호된다.
• 29 = p[C,B] > p[B,C] = 28이므로 후보자 C는 후보자 B보다 선호된다.
• 29 = p[C,D] > p[D,C] = 28이므로 후보자 C는 후보자 D보다 선호된다.
• 33 = p[B,D] > p[D,B] = 28이므로 후보자 B는 후보자 D보다 선호된다.

그러므로 슐츠 순위는 E > A > C > B > D 순이다.

구현

후보자 수를 C라고 하자. 그러면 플로이드-워셜 알고리듬으로 가장 강력한 경로의 강도를 계산할 수 있다. 아래의 파스칼 유사코드는 그러한 경로 판단을 나타낸 것이다.

• 입력: d[i,j]는 i후보를 j후보보다 강력하게 선호하는 투표자 수이다.
• 출력: p[i,j]는 i후보에서 j후보로 가는 가장 강력한 경로의 강도이다.

for i : = 1 to C
begin
   for j : = 1 to C
   begin
      if ( i ≠ j ) then
      begin
         if ( d[i,j] > d[j,i] ) then
         begin
            p[i,j] : = d[i,j]
         end
         else
         begin
            p[i,j] : = 0
         end
      end
   end
end

for i : = 1 to C
begin
   for j : = 1 to C
   begin
      if ( i ≠ j ) then
      begin
         for k : = 1 to C
         begin
            if ( i ≠ k ) then
            begin
               if ( j ≠ k ) then
               begin
                  p[j,k] : = max ( p[j,k], min ( p[j,i], p[i,k] ) )
               end
            end
         end
      end
   end
end

외부 링크

• 위키미디어 공용에 슐츠 방법 관련 미디어 분류가 있습니다.