쌍곡선

쌍곡선(雙曲線, 영어: hyperbola)은 평면 위에 있는 두 정점으로부터의 거리의 차가 일정한 점들의 집합으로 만들어지는 곡선을 말한다. 이때 기준이 되는 두 정점을 초점이라 한다.

쌍곡선

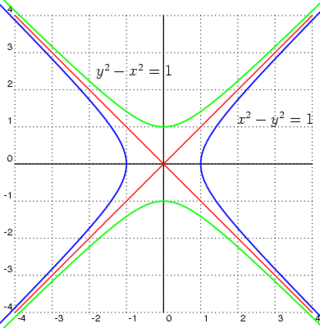
한초점이 극히 멀어질수록 쌍곡선은 포물선에 가까워진다. 한편 쌍곡선은 초점에서 멀어질수록 점근선이라고 불리는 직선에 가까워지며, 쌍곡선의 점근선은 두 개가 있다.

직교 좌표계상의 성질

쌍곡선은 두 개의 빨간색으로 나타낸 곡선을 말한다. 파란 점선으로 그려진 직선을 쌍곡선의 점근선(asymptotes)이라하며, 두 점근선은 쌍곡선의 중심 “C”에서 만난다. 두 초점은 각각 F₁ 과 F₂로 표시하였고, 이 두 초점을 연결하는 얇은 검은색 직선을 횡단축(traverse axis)이라 한다. 횡단축과 수직이며 쌍곡선의 중심을 지나는 검은색 얇은 직선을 켤레축(conjugate axis)이라 한다. 켤레축에 나란한(횡단축에 수직인) 두 개의 검은색 두꺼운 직선을 주선(directrices)라고 하며, 각각 D₁과 D₂로 표시되었다. 이심율(eccentricity) e는 쌍곡선 위의 한 점 P로부터, 한 초점까지의 거리와 주선까지의 거리의 비(녹색선 참고)와 같다. 두 꼭짓점은 각각 횡단축의 중심으로부터 ±’’a’’ 만큼 떨어져 있다. 다음은 변수들에 대한 설명이다:
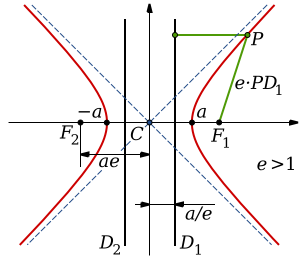
a — 중심 ‘’C’’로부터 꼭짓점 까지의 거리
b — 꼭짓점에서 횡단축에 수직하게 점근선까지 그은 선분의 길이
c — 중심 ‘’C’’에서 초점, F₁ 또는 F₂까지의 거리
θ — 점근선과 횡단축이 이루는 각.

초점이 ${\displaystyle x}$축 위에 있고, 원점을 중심으로 대칭인 쌍곡선은 직교 좌표계로 표현하면 다음과 같은 식이 된다.

${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}$

여기서 ${\displaystyle a,b}$는 고정된 상수값이다. ${\displaystyle \textstyle c={\sqrt {a^{2}+b^{2}}}}$일 때, 초점의 좌표는 다음과 같다.

${\displaystyle (-c,0),(c,0)}$

쌍곡선의 이심률(Eccentricity)은 다음과 같이 정의된다.

${\displaystyle {\frac {c}{a}}={\frac {\sqrt {a^{2}+b^{2}}}{a}}}$

쌍곡선의 점근선은 다음과 같게 된다.

${\displaystyle y=\pm {\frac {b}{a}}x}$

즉, 두 개의 직선이 된다.

이와 별도로, 두 축을 점근선으로 하는 쌍곡선은 다음과 같은 식으로 표현가능하다.

${\displaystyle xy=k}$

이 때, ${\displaystyle k}$는 고정된 상수이다.

쌍곡선과 이차 방정식

쌍곡선은 직교좌표계에서 이차방정식

${\displaystyle A_{xx}x^{2}+2A_{xy}xy+A_{yy}y^{2}+2B_{x}x+2B_{y}y+C=0}$

을 이용하여 정의할 수도 있다. 위의 이차 방정식의 계수 A_xx, A_xy, A_yy, B_x, B_y, and C 가

${\displaystyle D={\begin{vmatrix}A_{xx}&A_{xy}\\A_{xy}&A_{yy}\end{vmatrix}}<0\,}$

를 만족하면 위의 이차방정식은 쌍곡선을 나타낸다. 쌍곡선의 특별한 형태로 “퇴화 쌍곡선(degenerate hyperbola)를 들 수 있다.

퇴화 쌍곡선은 교차하는 두 직선으로 이루어지며, 위의 이차방정식의 계수를 원으로 하는 아래의 행렬식이

${\displaystyle \Delta$ :={\begin{vmatrix}A_{xx}&A_{xy}&B_{x}\\A_{xy}&A_{yy}&B_{y}\\B_{x}&B_{y}&C\end{vmatrix}}=0}

을 만족하면 위의 이차 방정식은 퇴화 쌍곡선을 나타낸다. 위의 행렬식 Δ를 원뿔곡선의 판별식이라 부르기도 한다.^[1]

쌍곡선의 중심 (x_c, y_c)은 식

${\displaystyle x_{c}=-{\frac {1}{D}}{\begin{vmatrix}B_{x}&A_{xy}\\B_{y}&A_{yy}\end{vmatrix}}}$

${\displaystyle y_{c}=-{\frac {1}{D}}{\begin{vmatrix}A_{xx}&B_{x}\\A_{xy}&B_{y}\end{vmatrix}}}$

에 의해 구할 수 있다.

쌍곡선의 중심이 원점이 되도록 평행이동하여 얻은 새로운 좌표계, ξ = x − x_c and η = y − y_c를 이용하여 쌍곡선의 방정식은

${\displaystyle A_{xx}\xi ^{2}+2A_{xy}\xi \eta +A_{yy}\eta ^{2}+{\frac {\Delta }{D}}=0}$

로 쓸 수 있다. 쌍곡선의 주축은 양의 ‘’x’’-축과 Φ의 각을 이룬다. 여기서 Φ는 다음과 같이 구할 수 있다.

${\displaystyle \tan 2\Phi ={\frac {2A_{xy}}{A_{xx}-A_{yy}}}}$

좌표축을 회전하여 ‘’x’’-축이 횡단축과 일치하도록 하면 앞의 이차방정식은 쌍곡선의 표준형 방정식

${\displaystyle {\frac {{x}^{2}}{a^{2}}}-{\frac {{y}^{2}}{b^{2}}}=1}$

으로 바꿀 수 있다.

기하학적 성질

쌍곡선 위의 모든 점은 두 초점과의 거리의 차가 일정하다.

다음은 직교 좌표계에서 어렵지 않게 증명가능하다.

• 쌍곡선 위의 모든 점은 두 초점과의 거리의 차가 일정하다.
• 한 초점에서 나온 빛은 쌍곡선에 반사되면 다른 초점에서 나온 빛처럼 보인다.
• 쌍곡선 위의 점에서 점근선에 수선의 발을 내리면 그 길이의 곱은 일정하다.
• 쌍곡선 위의 한 점을 지나며 두 점근선에 평행한 두 개의 직선과 두 점근선으로 이루어진 평행사변형의 면적은 일정하다.
• 초점이 일치하는 쌍곡선과 타원은 교점에서 각각의 접선이 수직이다.

접선의 방정식

쌍곡선 ${\displaystyle \textstyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}$ 위의 한 점 ${\displaystyle (x_{1},y_{1})}$에서의 접선의 방정식은 다음과 같다.

${\displaystyle {\frac {xx_{1}}{a^{2}}}-{\frac {yy_{1}}{b^{2}}}=1}$

또한, 기울기 ${\displaystyle m}$이 주어질 때의 접선의 방정식은 다음과 같다.

${\displaystyle y=mx\pm {\sqrt {a^{2}m^{2}-b^{2}}}}$