에지워스 박스

경제학에서 에지워스 박스(영어: Edgeworth box)는 때때로 에지워스-볼리 박스(영어: Edgeworth-Bowley box)라고도 불리며, 두 가지 상품 X와 Y, 그리고 두 명의 소비자로만 구성된 시장을 그래픽으로 표현한 것이다. 박스의 크기는 두 상품의 총량 Ω_x와 Ω_y이다.

그림 1. 에지워스 박스

소비자를 옥타비오(Octavio)와 애비(Abby)라고 하자. 박스의 오른쪽 상단 모서리는 옥타비오가 모든 상품을 소유하는 배분을 나타내고, 왼쪽 하단 모서리는 애비가 모든 상품을 소유하는 배분에 해당한다. 박스 내의 점들은 두 소비자 간에 상품을 배분하는 방식을 나타낸다.

시장의 행동은 소비자의 무차별 곡선에 의해 결정된다. 도표의 파란색 곡선은 옥타비오의 무차별 곡선을 나타내며, 그의 관점(즉, 왼쪽 하단에서 볼 때)에서 볼록하게 표시된다. 주황색 곡선은 애비에게 적용되며, 오른쪽 상단에서 볼 때 볼록하다. 오른쪽 위로 이동하면 옥타비오의 배분이 증가하고, 그는 더 바람직한 무차별 곡선으로 이동하는 반면, 애비는 덜 바람직한 무차별 곡선으로 이동한다.

볼록한 무차별 곡선은 일반적인 경우로 간주된다. 이는 각 상품이 다른 상품에 비해 수확 체감을 나타내는 것에 해당한다.

시장 내 교환은 초기 배분, 즉 부존자원(endowment)에서 시작된다.

에지워스 박스의 주요 용도는 일반균형이론의 주제들을 그래픽으로 시각화할 수 있는 형태로 소개하는 것이다. 이는 또한 쌍방 독점이 존재하는 상황에서 효율적인 결과로 나아가는 어려움을 보여줄 수도 있다.^[1] 후자의 경우, 이는 고유한 수치적 해를 허용하는 게임 이론의 교섭 문제의 전조 역할을 한다.^[2][3]

역사

에지워스 박스의 개발

에지워스 박스는 프랜시스 에지워스의 이름을 따서 명명되었으며,^[4] 그는 1881년 그의 저서 《Mathematical Psychics: An Essay on the Application of Mathematics to the Moral Sciences》에서 이를 발표했다.^[5] 에지워스의 원래 두 축 묘사는 빌프레도 파레토가 1906년 《정치경제학 매뉴얼》(Manual of Political Economy)에서 현재 익숙한 박스 다이어그램으로 발전시켰고, 이후 아서 라이언 볼리에 의해 대중화되었다. 이 다이어그램의 현대적 버전은 일반적으로 에지워스-볼리 박스라고 불린다.^[6]

경제 균형의 수학 이론

시장 경제에서의 균형에 대한 개념적 틀은 레옹 발라스^[7]에 의해 개발되었고 빌프레도 파레토에 의해 더욱 확장되었다.^[8] 이는 아브라함 왈드,^[9] 폴 새뮤얼슨,^[10] 케네스 애로, 제라르 드브뢰와 같은 20세기 수학 경제학자들에 의해 일반성과 엄격성에 주의를 기울여 연구되었다.^[11] 이는 왈드가 결정 이론에 더 큰 엄격함을 가져오려 했고 많은 수학자들이 선택 공리에 대한 의존도를 최소화하는 데 집중했던 더 넓은 운동의 일부였다.

왈라스적 시장 이론은 주어진 결론을 얻을 수 있는 가장 일반적인 전제를 찾는 데 많은 노력을 기울여 왔다. 전제를 강화하거나 약화시킬 수 있는 영역은 다음과 같다.

• 함수가 미분 가능한지 여부
• 무차별 곡선이 원시적인지 또는 효용 함수에서 파생될 수 있는지 여부
• 무차별 곡선이 볼록한지 여부

더 기술적인 성격의 가정도 이루어진다(예: 비가역성, 국소 비포화성, 등).

엄격함을 추구하는 것이 항상 이해하기 쉬운 것은 아니다. 이 글에서는 무차별 곡선을 원시적인 것으로 취급할 것이다. 처음에는 무차별 곡선을 볼록하고 미분 가능한 것으로 보고 내부 균형에 집중하겠지만, 이후 이러한 가정을 완화할 것이다.

시장 균형

그림 2. 에지워스 박스 시장

상품이 두 개뿐이므로 유효 가격은 상품 간의 교환 비율이다. 우리의 목표는 주어진 부존자원으로부터 더 이상 거래가 원치 않는 지점, 즉 시장 균형이 달성될 수 있는 가격을 찾는 것이다. 이 수량들은 그림 2에 나타난 두 소비자의 무차별 곡선에 의해 결정될 것이다.

매일 옥타비오와 애비가 시장에 나와 두 상품의 부존자원 (ω_x,ω_y )와 (Ω_x – ω_x , Ω_y – ω_y )를 가지고 온다고 가정한다. 이는 도표의 ω 위치에 해당한다. 두 소비자는 경쟁 시장 행동 하에서 서로 교환할 것이다. 이 가정은 완전 경쟁의 조건(무한한 수의 소비자를 포함)이 충족되지 않으므로, 어느 정도 불신을 유보해야 한다.

X 두 개가 Y 한 개와 교환된다면, 옥타비오와 애비의 거래는 예산선(budget line)이라고 불리는 실선 회색 선을 따라 어떤 지점으로 그들을 데려갈 것이다. (더 정확히 말하면, 예산선은 특정 가격에서의 교환을 통해 얻을 수 있는 배분을 나타내는, 부존자원 지점을 통과하는 직선으로 정의될 수 있다.) 다른 몇몇 가격에 대한 예산선도 그림 2에 점선과 파선으로 표시되어 있다.

그림 3. 에지워스 박스에서의 균형

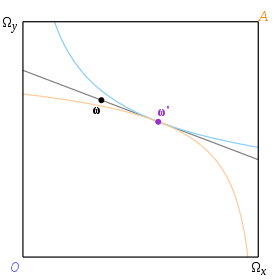
주어진 부존자원 ω에 해당하는 균형은 공통 접선을 가지며 이 접선이 ω를 통과하는 한 쌍의 무차별 곡선에 의해 결정된다. 우리는 '가격선'(price line)이라는 용어를 두 무차별 곡선의 공통 접선을 나타내는 데 사용할 것이다. 따라서 균형은 가격선이기도 한 예산선에 해당하며, 균형에서의 가격은 그 선의 기울기이다. 그림 3에서 ω는 부존자원이고 ω'는 균형 배분이다.

이러한 추론의 배경은 다음과 같다.

그림 4. 교차하는 무차별 곡선에 의한 이웃 분할

첫째, 박스 안의 어떤 지점도 애비의 무차별 곡선 중 하나와 옥타비오의 무차별 곡선 중 하나에 정확히 놓여야 한다. 곡선이 교차한다면(그림 4 참조), 즉각적인 인근 지역을 네 개의 영역으로 나누며, 그 중 하나(옅은 녹색으로 표시된)는 두 소비자 모두에게 더 바람직하다. 따라서 무차별 곡선이 교차하는 지점은 균형일 수 없으며, 균형은 접점이어야 한다.

둘째, 접점에서 시장에 존재할 수 있는 유일한 가격은 접선의 기울기에 의해 주어진 가격이다. 왜냐하면 오직 이 가격에서만 소비자들이 극히 작은 교환을 받아들일 의향이 있기 때문이다.

셋째(가장 어려운 점), 소비자들을 ω에서 균형으로 이끄는 경로상의 모든 교환은 동일한 가격으로 이루어져야 한다. 만약 이것이 받아들여진다면, 그 가격은 접점에서 작용하는 가격이어야 하고, 그 결과가 도출된다.

두 사람 경제에서는 모든 교환이 동일한 가격으로 이루어질 것이라는 보장은 없다. 그러나 에지워스 박스의 목적은 경쟁이 없을 때 발생할 수 있는 가격 결정(price fixing)을 설명하는 것이 아니라, 최소한의 경우에 경쟁 경제를 설명하는 것이다. 따라서 우리는 단 한 명의 애비와 옥타비오가 아니라, 각각의 무한한 복제본이 다른 시간에 동일한 부존자원을 가지고 시장에 와서 점진적으로 균형을 향해 협상하는 것을 상상할 수 있다. 새로 도착한 옥타비오는 균형에 가까워진 애비와 시장 가격으로 교환할 수 있으며, 새로 도착한 애비가 거의 만족한 옥타비오와 교환하는 한 숫자는 균형을 이룰 것이다. 대규모 경쟁 경제에서 교환이 작동하려면 동일한 가격이 모두에게 적용되어야 한다. 따라서 교환은 우리가 정의한 가격선을 따라 배분을 이동시켜야 한다.^[12]

따라서 경쟁 균형을 찾는 작업은 주어진 점을 통과하는 접선을 갖는 두 무차별 곡선 간의 접점을 찾는 작업으로 귀결된다. 제안 곡선의 사용(아래 설명)은 이를 수행하는 체계적인 절차를 제공한다.

파레토 집합

그림 5. 두 접하는 무차별 곡선에 의한 박스 분할

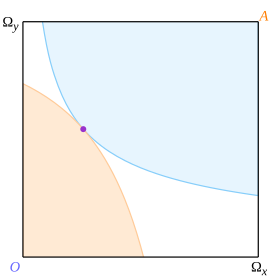
어떤 상품 배분이 다른 배분보다 한 소비자에게는 더 바람직하고 다른 소비자에게는 나쁘지 않을 경우, 그 배분은 다른 배분을 '파레토 우위'한다고 말한다. 어떤 배분이 다른 어떤 배분도 파레토 우위하지 않을 경우, 그 배분은 '파레토 최적'(또는 '파레토 효율적')이라고 말한다. 파레토 최적 배분들의 집합은 파레토 집합(Pareto set, 또는 '효율적 궤적')이라고 알려져 있다.

그림 5에 나타난 바와 같이 각 소비자에 대한 한 쌍의 접하는 곡선을 고려하자. 접점은 보라색 점으로 표시되어 있다. 그러면 볼록성은 곡선이 접점 이외의 지점에서 교차할 수 없음을 보장하며, 따라서 박스는 3개의 영역으로 나뉜다. 옅은 파란색 영역은 옥타비오에게는 접점보다 더 바람직하지만 애비에게는 더 나쁘다. 옅은 주황색 영역은 애비에게는 더 바람직하지만 옥타비오에게는 더 나쁘다. 그리고 흰색 영역은 둘 다에게 더 나쁘다. 경계에도 유사한 고려 사항이 적용된다. 따라서 접점은 파레토 최적이다.

그림 6. 에지워스 박스의 파레토 집합 (보라색 선)

따라서 파레토 집합은 곡선들의 접점들의 궤적이다. 이는 옥타비오의 원점(O)과 애비의 원점(A)을 연결하는 선이다. 그림 6에 예시가 나와 있으며, 보라색 선은 두 소비자의 무차별 곡선에 해당하는 파레토 집합이다.

에지워스 박스의 여러 대상을 설명하는 용어는 다양하게 사용된다. 파레토 집합 전체를 때때로 계약 곡선이라고 부르기도 하지만, 마스-콜렐 외(Mas-Colell et al.)는 계약 곡선의 정의를 파레토 집합 중 애비와 옥타비오 모두에게 초기 부존자원만큼 혹은 그 이상으로 나은 점들로 제한한다. 마틴 오스본(Martin Osborne)과 아리엘 루빈스타인(Ariel Rubinstein)^[13]과 같이 게임 이론적 성향이 강한 다른 저자들은 파레토 집합의 해당 부분을 각 소비자에게 초기 부존자원만큼 혹은 그 이상으로 좋은 부분에 대해 핵심이라는 용어를 사용한다.

파레토 집합은 소비자의 무차별 곡선이 접하는 점들의 집합이므로, 각 소비자의 한계대체율이 다른 사람의 한계대체율과 동일한 점들의 집합이기도 하다.^[14]

후생경제학의 제1 기본 정리

무차별 곡선의 접점이 파레토 최적점이라는 것을 보았지만, 이전에 경제 균형이 무차별 곡선이 공통 가격선에 접하는 점이라는 것도 보았다. 따라서 균형은 정확히 파레토 최적점이다.

이 주장은 곡선이 미분 불가능하거나 균형이 경계에 있더라도 하나의 제약하에 적용된다. 균형 조건은 더 이상의 교환이 일어나지 않는 것이고, 더 이상의 교환이 일어나지 않는 조건은 한 소비자를 해치지 않고 다른 소비자에게 이득을 주는 움직임의 방향이 없다는 것이다. 이것은 파레토 최적의 정의와 동등하다.^[15]

제약은 균형이 국소적 개선이 불가능하다는 것을 의미한다는 점이다. 즉, 그 지점이 '국소적으로' 파레토 최적이라는 것이다. 그러나 파레토 최적은 오늘날 정의상 전역적인 것으로 간주된다.^[16] 따라서 무차별 곡선의 특성이 비전역적 최적점(볼록한 경우에는 발생할 수 없음)이 발생하도록 허용한다면, 균형이 파레토 최적이 아닐 수도 있다.

완전 경쟁은 이 정리의 전제 조건이 아니다. 소비자들이 자유롭게 교환할 수 있고, 상호 수용 가능한 교환이 없을 때까지 계속 그렇게 한다면 균형에 도달할 것이고 (적어도 '국소적으로') 파레토 최적이 될 것이다.^[17]

후생경제학의 제2 기본 정리

그림 7. 제2 후생정리

이제 그림 7에 표시된 것처럼 소비자들이 부존자원 ω를 가진 경제를 고려해 보자. 자유 시장은 스스로 그들을 ω'로 이끌 것이다. 하지만 박스 내의 다른 위치, 예를 들어 α'가 사회적으로 더 바람직하다고 간주된다고 가정해 보자. 우리는 사회적으로 바람직한 위치가 파레토 최적이라고 가정할 수 있다.

(도표에 점선으로 표시된) 가격선을 실질 소득의 다른 분배에 해당하는 것으로 생각할 수 있으며, 그 선을 따라 이동하는 것은 소득이 고정된 상태에서 자원의 재할당으로 볼 수 있다.

그렇다면 사회를 원하는 지점 α'에 재배치하기 위해 정부가 옥타비오가 (α'_x,α'_y)를 소유하고 애비가 나머지를 소유하는 방식으로 자원을 재분배할 필요는 없다. 대신, 경제를 α'를 통과하는 가격선 상의 어떤 지점(예: α)으로 자원을 재할당한 다음, 시장이 스스로 균형을 찾도록 두는 것으로 충분하다. 실제로, 정부가 바람직한 소득 분배를 인식하는 한, 자원의 최적 배분에 대한 어떤 아이디어를 가질 필요도 없다.

더 일반적인 경제에 대한 진술에서, 이 정리는 α'가 화폐 이전(monetary transfer) 후 시장 교환의 자유로운 작용을 통해 도달될 수 있다고 말하는 것으로 받아들여질 것이다. 그러나 에지워스 박스에는 화폐가 없다.

두 번째 기본 정리는 사회의 문제를 해결하기 위한 청사진을 제공하지 않는다. 정부는 옥타비오와 애비 간에 자원을 재할당하여 그들을 ω에서 α로 이동시킬 수 있으며, 그 결과 손해를 보는 사람은 다음 날 시장에 덜 내놓기로 결정할 수 있다. 두 번째 기본 정리는 재할당으로 인해 발생하는 왜곡을 고려하지 않는다.^[18]

제안 곡선

그림 8. 다른 예산선에서 선호되는 지점들

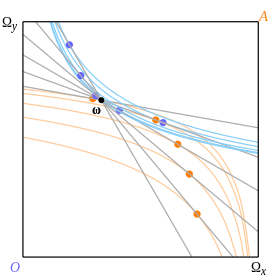
제안 곡선(Offer curve)은 균형점을 찾는 수단을 제공하며, 균형점의 존재 및 유일성을 조사하는 데도 유용하다.

두 소비자에 대해 각각 하나씩, 부존자원에 따라 달라지는 두 개의 곡선을 박스 안에 그릴 수 있다. 우리는 예산선을 ω를 중심으로 회전시키고, 그림 8의 색깔 있는 점들로 표시된 대로 두 소비자가 선을 따라 가장 선호하는 점들을 추적한다. 이 점들은 선이 그들 자신의 무차별 곡선에 접하는 점들이다.

그림 9. 제안 곡선

소비자가 가장 선호하는 점들의 궤적이 바로 그의 제안 곡선이다. 그림 9는 옥타비오의 제안 곡선을 짙은 파란색으로, 애비의 제안 곡선을 갈색으로 보여준다. 이들은 지점 ω'에서 만나고, 회색으로 그려진 균형 예산선은 이 지점을 통과하는 선이다. 두 소비자의 ω'를 통과하는 무차별 곡선은 더 옅은 색으로 표시되어 있다.

제안 곡선은 반드시 부존자원 점 ω를 통과한다. 애비를 예로 들면, 그녀의 무차별 곡선 중 하나가 ω를 통과해야 하고, 예산선은 이곳에서 무차별 곡선과 동일한 기울기를 가지도록 선택될 수 있으며, 따라서 ω는 이 선에 대해 가장 선호되는 점이 된다.

결과적으로 두 소비자의 제안 곡선은 필연적으로 ω에서 교차한다. 그러나 이러한 현상을 가능하게 하는 속성은 ω가 서로 다른 기울기를 가진 예산선과 일치하는 유일한 가능한 교차점이라는 것이며, 따라서 반드시 균형을 구성하는 것은 아니다.

ω 이외의 지점에서 제안 곡선이 교차하면 안정적인 균형이 결정된다. 두 제안 곡선이 부존자원 지점에서 접한다면, 이 지점은 실제로 균형이며 그들의 공통 접선은 해당 예산선이다.^[19]

제안 곡선에 대한 용어

제안 곡선은 빌프레도 파레토가 처음 사용했다. 그의 《Manuale/Manuel》 3장 §97을 참조하라. 그는 이를 '교환 곡선'(linee dei baratti / lignes des échanges)이라고 불렀으며, 옥타비오가 예산선을 따라 선호하는 배분을 '균형점'이라고 불렀다.

이 선호 배분은 오늘날 때때로 옥타비오의 '수요'라고 불리는데, 이는 대칭적인 사실을 비대칭적으로 기술하는 것이다. 배분은 옥타비오의 보유량뿐만 아니라 애비의 보유량도 결정하므로, 수요만큼이나 공급이기도 하다.

'Offre'는 프랑스어로 '공급'을 의미하므로, 제안 곡선을 수요의 궤적이라고 부르는 것은 공급 곡선을 수요의 궤적이라고 부르는 것과 마찬가지이다.

균형의 유일성

그림 10. 다중 균형이 있는 에지워스 박스

그림 11. 다중 균형이 있는 에지워스 박스 (상세)

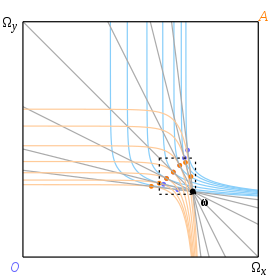
경제적 고려 사항에 따르면 주어진 부존자원을 통해 공유 접선이 존재하고 무차별 곡선의 형태가 병리적이지 않다면 접점은 유일할 것이라고 가정할 수 있다. 그러나 이는 사실이 아닌 것으로 밝혀졌다. 균형의 유일성 조건은 광범위한 연구의 대상이었다. 일반균형이론을 참조하라.

그림 9와 10은 Mas-Colell 등의 예시를 보여주며, 이 예시에서는 부존자원 지점 ω에 세 가지 다른 균형이 해당한다. 무차별 곡선은 다음과 같다.

${\displaystyle \quad x-{\tfrac {1}{8}}y^{-8}=u}$ (옥타비오)

${\displaystyle \quad y-{\tfrac {1}{8}}x^{-8}=u}$ (애비).

무차별 곡선은 박스를 채우지만, 몇몇 대표적인 예산선에 접하는 경우에만 표시된다. 그림 11에 그려진 제안 곡선은 큰 회색 점으로 표시된 세 지점에서 교차하며, 이는 각각 1⁄2, 1, 2의 교환율에 해당한다.

일반화

균형의 속성에 대한 초기 검토는 접선이라는 암묵적 정의에 기반을 두었고, 볼록성은 암묵적으로 가정된 것으로 보인다.^[20] 균형이 달성될 것이라는 데는 의심의 여지가 없었다. 경사 하강법은 균형으로 이끌 것이다. 그러나 결과는 일반성을 결여했다.

경계 균형과 미분 불가능한 곡선

그림 12. 경계 균형이 있는 박스의 가격선

케네스 애로와 제라르 드브뢰는 1951년에 독립적으로 논문을 발표하여 균형 정리의 미분 증명에 대한 한계에 주목했다.^[21] 애로는 특히 경계에서의 균형으로 인한 어려움을 언급했고, 드브뢰는 미분 불가능한 무차별 곡선 문제를 언급했다.

포괄적인 설명을 목표로 하지 않고도, 이러한 경우에 우리의 방법을 어떻게 확장할 수 있는지 직관적으로 쉽게 알 수 있다. 우리는 곡선에 접하는 모든 선을 포함하도록 접선의 개념을 확장해야 한다. 즉, 미분 미적분학의 의미가 아닌 어원학적 의미의 접선이다. 그림 12의 예시에서 접점(point of contact)을 통과하는 합법적인 가격선의 호가 있는데, 각 선은 박스 안에서 무차별 곡선을 자르지 않고 접하며, 따라서 주어진 부존자원에 대해 가능한 균형의 범위가 존재한다.

경쟁 균형

그림 12의 균형은 곡선들이 서로 진정한 접선을 이루는 지점이 아니다. 그러나 이들은 접선을 통한 정의를 일반화하는 속성을 가지고 있는데, 그것은 두 곡선이 직선에 의해 국소적으로 분리될 수 있다는 것이다.

애로와 드브뢰는 1951년의 (독립적인) 논문에서 서로 동일한 방식으로 균형을 정의했으며, 그들의 정의에 대한 출처나 근거를 제공하지 않았다. 그들은 1954년의 공동 논문(균형의 존재에 관한)에서 그들의 정의를 유지했다.^[22] 새로운 정의는 수학적 기법을 미분 미적분학에서 볼록 집합 이론으로 변경해야 했다.

그들의 정의는 사실상 다음과 같았다: 부존자원 ω로부터 달성 가능한 균형은 배분 x와 x와 ω를 통과하는 예산선으로 구성되며, 이 예산선을 따라 어느 소비자도 x보다 (엄격하게) 선호하는 지점이 없어야 한다. 이 속성을 만족하는 배분과 선의 쌍을 '왈라스 균형' 또는 경쟁 균형이라고 한다.

그림 13. '국소적' 균형

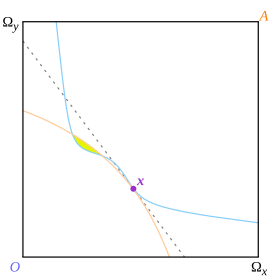
이 정의의 예산선은 두 소비자의 무차별 곡선을 분리하는 선이지만, 국소적으로가 아니라 전역적으로 분리한다. 애로와 드브뢰는 왜 전역적 분리를 요구하는지 설명하지 않는데, 이는 그들의 증명을 더 쉽게 만들었을 수도 있지만 예상치 못한 결과를 초래할 수 있다. 그림 13에서 지점 x는 접점이며, 무차별 곡선이 점선 가격선에 의해 국소적으로 분리되는 지점이기도 하다. 그러나 전역적으로 분리되지 않으므로, 애로와 드브뢰의 정의에 따르면 이 지점은 균형이 아니다.

그림 14. '경쟁 균형'이 아닌 파레토 최적

그림 14에서 지점 x는 경쟁 균형의 정의를 만족하지 않는 파레토 최적이다. 경제가 그러한 지점에 정착할 것인지에 대한 질문은 주어진 균형 정의를 만족하는지 여부와는 완전히 별개이다. 분명히 이 경우 경제는 실제로 그 지점에 정착할 것이다.

애로와 드브뢰는 항상 무차별 곡선의 볼록성을 그들의 '가정'에 포함했다. '가정'이라는 용어는 정의와 정리의 기초가 되는 전제, 또는 후자에만 필요한 전제를 의미할 수 있는 모호한 용어이다. 그들의 정의가 곡선이 비볼록할 때 존재할 수 있는 모든 균형을 포함하지 않는다는 점을 고려하면, 그들이 볼록성 가정을 전자 의미로 의도했을 가능성이 있다. 그렇든 아니든, 이 정의는 영역의 제한 없이 널리 채택되었다.

때때로 증명에서 볼록성을 가정하지 않고도 그들의 정의하에서 결과가 도출될 수 있음이 밝혀졌다 (후생경제학의 제1 기본 정리가 그 예이다).

경쟁 균형의 존재

일부 경제에서는 균일한 가격으로 교환하여 주어진 부존자원으로부터 도달할 수 있는 정착점이 없을 것이다. 따라서 경쟁 균형의 정의를 만족하는 정착점은 존재하지 않는다. 그림 14와 같은 패턴의 곡선 군이 그 예시이다.

후생경제학의 기본 정리

균형이 '경쟁 균형'으로 정의되면, 무차별 곡선이 볼록할 필요가 없어도 제1 기본 정리를 증명할 수 있다. 즉, 어떤 경쟁 균형이든 (전역적으로) 파레토 최적이다. 그러나 증명은 더 이상 명확하지 않으며, 후생경제학의 기본 정리에 대한 문서를 참조해야 한다.

동일한 결과는 균형의 접선 정의 하에서는 (비볼록 무차별 곡선과 함께) 성립하지 않는 것으로 간주되었을 것이다. 그림 13의 지점 x는 노란색 영역이 파레토 우위하므로 (전역적으로) 최적이 아닌 균형으로 간주되었을 것이다.

균형의 달성 가능성이 의심스러워졌기 때문에 결과가 강화되었다고는 할 수 없다. 그림 13에서 지점 x는 '경쟁 균형'이 아닐 수 있지만, 경제는 그곳에 갇혀 '진정한'(그리고 파레토 최적의) 균형에 도달하지 못할 수 있다.

균형이 실제로 달성될 것이라는 점은 항상 제1 후생정리의 핵심으로 간주되었다. 러너(Lerner)의 정리에 대한 해석은 "다행히도 상품의 최적 배분은 자동으로 달성될 수 있다"는 것이었다.^[23] 그러나 국소 최적점이 존재할 때 전역 최적점이 달성될 것이라고 보장할 수 있는 것은 없다. 만약 균형의 개념이 x와 같은 국소 최적점을 포함한다면, 균형은 달성 가능하지만 차선책일 수 있다. 만약 그러한 점들이 제외된다면, 균형은 최적일 수 있지만 달성 불가능할 수 있다.

비볼록성으로 인한 차이는 제2 기본 정리를 살펴볼 때 더욱 깊어진다. 모든 파레토 최적점이 경쟁 균형인 것은 아니다 (비록 여전히 경제의 정착점일 수 있더라도). 결과적으로 이 정리는 선호의 볼록성을 전제로 하거나, '균형'이 위에서 정의한 '경쟁 균형'으로 이해되지 않도록 명시되어야 한다.