정규 언어

정규 언어(regular language), 합리적 언어(rational language)^[1][2]는 이론 전산학, 형식 언어 이론에서 정규 표현식을 이용하여 표현할 수 있는 형식 언어이다.

정규 언어는 유한 상태 기계가 인지하는 언어로 정의할 수도 있다. 정규 표현식과 유한 상태 기계의 등가성은 클레이니의 정리로 알려져 있다.^[3] 촘스키 위계에서 정규 언어는 3형 문법(정규 문법)에 의해 생성되는 언어로 정의된다.

정규 언어는 입력 구문 분석(파싱)과 프로그래밍 언어 설계에 매우 유용하다.

정의

 정규 표현식 문서를 참고하십시오.

알파벳 Σ 위의 정규 언어의 집합은 다음과 같이 재귀적으로 정의할 수 있다.

• 공집합 Ø은 정규 언어이다.
• 각 글자 a ∈ Σ에 대해 한원소집합 {a}는 정규 언어이다.
• A가 정규 언어이면, 클레이니 스타를 붙인 A^*도 정규 언어이다. (따라서 빈 문자열로만 이루어진 {ε}도 정규 언어이다.)
• A와 B가 정규 언어이면, 합집합 A ∪ B와 문자열 연결 AB도 정규 언어이다.
• 그 밖의 언어는 정규 언어가 아니다.

예시

유한한 언어는 모두 정규 언어이다. 특히 {ε} = Ø^*도 정규 언어이다. 알파벳 {a, b} 위의 정규 언어의 예로는 a를 짝수 개 포함하는 모든 문자열의 집합이나, a 여러 개 뒤에 b 여러 개가 오는 꼴인 모든 문자열의 집합 따위가 있다.

정규 언어가 아닌 언어의 예로 { aⁿbⁿ | n ≥ 0 }이 있다.^[4] 직관적으로 설명하면, 유한 상태 기계의 기억력은 유한하기 때문에 a가 몇 번 나왔는지 정확히 기억할 수 없으므로, 유한 상태 기계는 이 언어를 인지할 수 없기 때문이다.

동등한 형식화

형식언어 L이 정규 언어라는 것은 다음과 동치이다.

1. L은 정규 표현식으로 나타낼 수 있다. (위의 정의)
2. L은 비결정적 유한 상태 기계가 인지하는 언어이다.^[a][b]
3. L은 결정적 유한 상태 기계가 인지하는 언어이다.^[c][d]
4. L은 정규 문법이 생성하는 언어이다.^[e][f]
5. L은 교대 유한 상태 기계(alternating finite automaton)가 인지하는 언어이다.
6. L은 양쪽 유한 상태 기계(two-way finite automaton)가 인지하는 언어이다.
7. L은 접두사 문법(prefix grammar)이 생성하는 언어이다.
8. L은 읽기 전용 튜링 기계가 인지하는 언어이다.
9. L은 일변수(monadic) 2차 논리에서 정의할 수 있는 언어이다. (뷔히-엘고트-트라크텐브로트 정리)^[5]

닫힘 성질

정규 언어의 집합은 여러 연산에 대해 닫혀 있다. K와 L이 정규 언어라면, 다음도 정규 언어이다.

• 불 연산: 합집합 K ∪ L, 교집합 K ∩ L, 여집합 L, 차집합 K - L.^[6]
• 정규식 연산: K ∪ L, 문자열 연결 KL, 클레이니 스타 L^*.^[7]
• h가 문자열 준동형사상일 때, h(L)과 h^-1(L).
• 임의의 언어 B에 대해, (오른쪽) 몫 B/L.
• 거울상 L^R.^[8]

결정 가능성

결정적 유한 상태 기계 A와 B가 주어졌을 때, 두 기계가 같은 언어를 인지하는지 결정할 수 있다.^[9] 따라서 위의 닫힘 성질을 이용하면 두 기계가 인지하는 정규 언어 L_A와 LB에 대해 다음 문제를 결정할 수 있다.

• 포함: L_A ⊆ L_B인가?^[g]
• 서로소: L_A ∩ L_B = Ø인가?
• 공집합: L_A = Ø인가?
• 전체집합: L_A = Σ^*인가?
• 소속: 주어진 a ∈ Σ^*에 대해, a ∈ L_A인가?

촘스키 위계에서의 위치

촘스키 위계에서 정규 언어의 위치

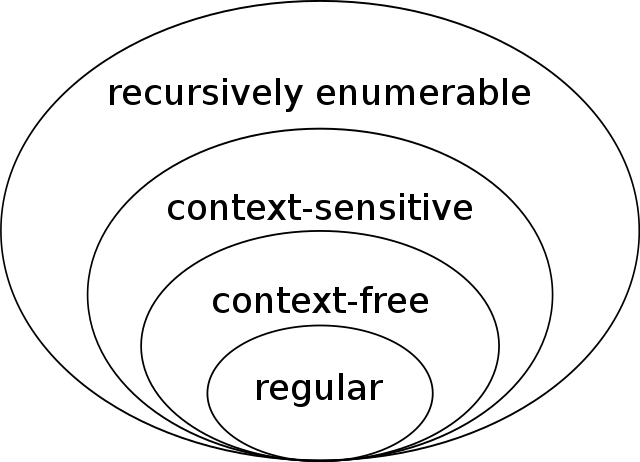
모든 정규 언어는 문맥 자유 언어이다. 그러나 반대는 성립하지 않는다. { aⁿbⁿ | n ≥ 0 }는 문맥 자유 언어이지만 정규 언어가 아닌 예이다.

주어진 언어가 정규 언어인지 알아보려면 흔히 마이힐-네로드 정리나 펌핑 보조정리를 사용한다. 그 밖에 정규 언어의 닫힘 성질이나 콜모고로프 복잡도를 사용하는 방법도 있다.^[10]

내용주

1. 1 ⇒ 2: 톰슨 구성
2. 2 ⇒ 1: 클레이니 알고리즘 또는 아덴 보조정리
3. 2 ⇒ 3: 멱집합 구성
4. 3 ⇒ 2: 모든 결정적 유한 상태 기계는 비결정적 유한 상태 기계이므로.
5. 2 ⇒ 4: Hopcroft, Ullman (1979), Theorem 9.2, p.219 참조
6. 4 ⇒ 2: Hopcroft, Ullman (1979), Theorem 9.1, p.218 참조
7. L_A ∩ L_B = L_A인지 확인하면 된다.