정적 단일 대입 형식

컴파일러 설계에서 정적 단일 대입 형식(Static single-assignment form, SSA 형식 또는 단순히 SSA로 약칭)은 각 변수가 정확히 한 번 할당되는 중간 표현 (IR)의 한 유형이다. SSA는 LLVM, GNU 컴파일러 모음 및 많은 상업용 컴파일러를 포함하여 명령형 언어에 대한 대부분의 고품질 최적화 컴파일러에서 사용된다.

프로그램을 SSA 형식으로 변환하기 위한 효율적인 알고리즘이 있다. SSA로 변환하기 위해 원래 IR의 기존 변수들은 버전으로 분할되며, 일반적으로 원래 이름에 아래첨자가 붙어 각 정의가 고유한 버전을 갖도록 한다. 두 제어 흐름 경로의 조인 지점에 변수의 새 버전에 할당하는 추가 문도 도입해야 할 수 있다. SSA 형식에서 기계 코드로 변환하는 것도 효율적이다.

SSA는 변수의 사용을 볼 때 변수가 값을 받을 수 있는 곳이 한 곳뿐이므로 사용-정의 체인 결정과 같이 최적화에 필요한 수많은 분석을 쉽게 수행할 수 있도록 한다. 대부분의 최적화는 SSA 형식을 유지하도록 조정될 수 있으므로 추가 분석 없이 한 최적화를 다른 최적화 후에 수행할 수 있다. SSA 기반 최적화는 일반적으로 비SSA 형식의 이전 최적화보다 효율적이고 강력하다.

스킴 및 ML과 같은 함수형 언어 컴파일러에서는 일반적으로 연속 전달 방식(CPS)이 사용된다. SSA는 비지역 제어 흐름을 제외한 CPS의 잘 정돈된 부분 집합과 형식적으로 동일하므로, 한 방식으로 공식화된 최적화 및 변환은 일반적으로 다른 방식에도 적용된다. CPS를 중간 표현으로 사용하는 것은 고차 함수 및 프로시저 간 분석에 더 자연스럽다. 또한 CPS는 call/cc를 쉽게 인코딩할 수 있는 반면, SSA는 그렇지 않다.^[1]

역사

SSA는 1980년대에 IBM의 여러 연구원들에 의해 개발되었다. 팀의 핵심 멤버인 케네스 제이덱(Kenneth Zadeck)은 개발이 계속됨에 따라 브라운 대학교로 자리를 옮겼다.^[2][3] 1986년 논문에서는 변수가 단일 정적 할당을 갖도록 birthpoints, identity assignment, 그리고 변수 이름 변경을 소개했다.^[4] 잔 페란테와 로널드 사이트론(Ronald Cytron)의 1987년 후속 논문^[5]에서는 이전 논문에서 수행된 이름 변경이 스칼라에 대한 모든 잘못된 의존성을 제거한다는 것을 증명했다.^[3] 1988년에 배리 로젠(Barry Rosen), 마크 N. 웨그먼, 케네스 제이덱은 identity assignment를 Φ-함수로 대체하고 "정적 단일 할당 형식"이라는 이름을 도입했으며, 현재 널리 사용되는 SSA 최적화를 시연했다.^[6] Φ-함수라는 이름은 로젠이 "가짜 함수"(phony function)의 더 출판 가능한 버전으로 선택했다.^[3] 알페른(Alpern), 웨그먼, 제이덱은 또 다른 최적화를 제시했지만, "정적 단일 할당"이라는 이름을 사용했다.^[7] 마지막으로 1989년에 로젠, 웨그먼, 제이덱, 사이트론, 페란테는 프로그램을 SSA 형식으로 변환하는 효율적인 방법을 찾아냈다.^[8]

장점

SSA의 주요 유용성은 변수의 속성을 단순화하여 다양한 컴파일러 최적화의 결과를 동시에 단순화하고 개선하는 방식에 있다. 예를 들어, 다음 코드를 고려해보자:

y := 1
y := 2
x := y

사람은 첫 번째 할당이 불필요하며, 세 번째 줄에서 사용되는 y의 값은 y의 두 번째 할당에서 비롯된다는 것을 알 수 있다. 프로그램은 이를 결정하기 위해 도달 정의 분석을 수행해야 한다. 하지만 프로그램이 SSA 형식이라면 이 두 가지는 즉각적으로 알 수 있다:

y1 := 1
y2 := 2
x1 := y2

SSA 사용으로 가능해지거나 크게 향상된 컴파일러 최적화 알고리즘은 다음과 같다:

• 상수 폴딩 – 계산을 런타임에서 컴파일 시간으로 변환하는 것. 예를 들어, a=3*4+5; 명령을 a=17;처럼 처리한다.
• 값 범위 전파^[9] – 계산이 가질 수 있는 잠재적 범위를 미리 계산하여 분기 예측을 미리 생성할 수 있게 한다.
• 희소 조건부 상수 전파 – 일부 값의 범위 확인을 통해 테스트가 가장 가능성 있는 분기를 예측할 수 있도록 한다.
• 데드 코드 제거 – 결과에 영향을 미치지 않는 코드를 제거한다.
• 전역 값 번호 매기기 – 동일한 결과를 생성하는 중복 계산을 대체한다.
• 부분 중복성 제거 – 프로그램의 일부 분기에서 이전에 수행된 중복 계산을 제거한다.
• 강도 감소 – 비용이 많이 드는 작업을 더 저렴하지만 동등한 작업으로 대체하는 것. 예를 들어, 2의 거듭제곱으로 정수 곱셈 또는 나눗셈을 잠재적으로 더 저렴한 왼쪽 시프트(곱셈용) 또는 오른쪽 시프트(나눗셈용)로 대체한다.
• 레지스터 할당 – 제한된 수의 기계 레지스터를 계산에 어떻게 사용할 수 있는지 최적화한다.

SSA로 변환

일반 코드를 SSA 형식으로 변환하는 것은 주로 각 할당의 대상(target)을 새 변수로 교체하고, 변수의 각 사용을 해당 지점에 도달하는 변수의 "버전"으로 교체하는 문제이다. 예를 들어, 다음 제어 흐름 그래프를 고려해 보자:

SSA로 변환하기 전의 제어 흐름 그래프 예시

"x ${\displaystyle \leftarrow }$ x - 3"의 왼쪽에 있는 이름을 변경하고 x의 다음 사용을 그 새 이름으로 변경해도 프로그램은 변경되지 않는다. 이것은 SSA에서 두 개의 새로운 변수 x₁과 x₂를 생성하여 활용될 수 있는데, 각각 한 번만 할당된다. 마찬가지로, 다른 모든 변수에 식별하는 아래첨자를 부여하면 다음과 같다:

부분적으로 SSA로 변환된 제어 흐름 그래프 예시

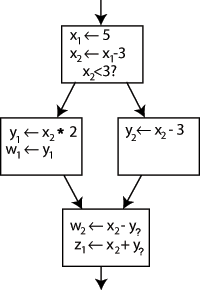
각 사용이 어떤 정의를 참조하는지 명확하지만, 한 가지 경우를 제외하고는 명확하다. 즉, 아래 블록의 y의 두 사용은 제어 흐름이 어떤 경로를 택했는지에 따라 y₁ 또는 y₂를 참조할 수 있다.

이 문제를 해결하기 위해 마지막 블록에 Φ(Phi) 함수라는 특수 문을 삽입한다. 이 문은 과거의 제어 흐름에 따라 y₁ 또는 y₂를 "선택"하여 y₃이라는 y의 새로운 정의를 생성한다.

완전히 SSA로 변환된 제어 흐름 그래프 예시

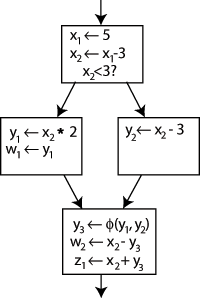
이제 마지막 블록은 간단히 y₃을 사용하고, 어떤 방식으로든 올바른 값이 얻어질 것이다. x에 대한 Φ 함수는 필요하지 않다. x의 한 가지 버전, 즉 x₂만 이 위치에 도달하고 있으므로 문제가 없다(다시 말해, Φ(x₂,x₂)=x₂).

임의의 제어 흐름 그래프가 주어졌을 때, Φ 함수를 어디에 어떤 변수에 삽입해야 할지 파악하기 어려울 수 있다. 이 일반적인 질문에는 지배 프론티어(dominance frontiers)라는 개념을 사용하여 효율적으로 계산할 수 있는 해결책이 있다(아래 참조).

Φ 함수는 대부분의 기계에서 기계 연산으로 구현되지 않는다. 컴파일러는 각 선행 블록의 끝에 "이동(move)" 연산을 삽입하여 Φ 함수를 구현할 수 있다. 위 예시에서 컴파일러는 중간 왼쪽 블록의 끝에 y₁에서 y₃으로의 이동을, 중간 오른쪽 블록의 끝에 y₂에서 y₃으로의 이동을 삽입할 수 있다. 이러한 이동 연산은 컴파일러의 레지스터 할당 절차에 따라 최종 코드에 포함되지 않을 수도 있다. 그러나, 와이드 이슈 머신에서 발생할 수 있는 것처럼 동시 작업이 투기적으로 Φ 함수의 입력을 생성하는 경우에는 이 접근 방식이 작동하지 않을 수 있다. 일반적으로 와이드 이슈 머신은 컴파일러가 Φ 함수를 구현하기 위해 이러한 상황에서 사용하는 선택 명령어를 가지고 있다.

지배 프론티어를 이용한 최소 SSA 계산

제어 흐름 그래프에서, 노드 A가 다른 노드 B를 엄격히 지배한다고 하는 것은 A를 거치지 않고는 B에 도달하는 것이 불가능하다는 것을 의미한다. 다시 말해, 노드 B에 도달하면 A가 실행되었다고 가정할 수 있다. A가 B를 지배한다(또는 B가 A에 지배된다)고 하는 것은 A가 B를 엄격히 지배하거나 A=B인 경우를 말한다.

노드 A에게 제어를 전달하는 노드는 A의 직접 선행자라고 불린다.

노드 A의 지배 프론티어는 A가 B를 엄격히 지배하지 않지만, B의 직접 선행자 중 일부를 지배하는 노드 B의 집합이다. 이들은 여러 제어 경로가 다시 하나의 경로로 합쳐지는 지점이다.

예를 들어, 다음 코드에서:

[1] x = random()
if x < 0.5
    [2] result = "heads"
else
    [3] result = "tails"
end
[4] print(result)

노드 1은 노드 2, 3, 4를 엄격히 지배하며 노드 4의 직접 선행자는 노드 2와 3이다.

지배 프론티어는 Φ 함수가 필요한 지점을 정의한다. 위 예시에서, 제어가 노드 4로 전달될 때, 사용되는 result의 정의는 제어가 노드 2 또는 3에서 전달되었는지에 따라 달라진다. Φ 함수는 지배자에서 정의된 변수에는 필요하지 않다. 적용될 수 있는 유일한 정의만 있기 때문이다.

각 노드의 지배 프론티어를 찾는 효율적인 알고리즘이 있다. 이 알고리즘은 1991년 론 사이트론(Ron Cytron), 잔 페란테(Jeanne Ferrante) 등이 쓴 "Efficiently Computing Static Single Assignment Form and the Control Graph"에서 처음으로 설명되었다.^[10]

라이스 대학교의 키스 D. 쿠퍼(Keith D. Cooper), 티모시 J. 하비(Timothy J. Harvey), 켄 케네디(Ken Kennedy)는 그들의 논문 "A Simple, Fast Dominance Algorithm"에서 한 알고리즘을 설명한다.^[11]

for each node b
    dominance_frontier(b) := {}
for each node b
    if the number of immediate predecessors of b ≥ 2
        for each p in immediate predecessors of b
            runner := p
            while runner ≠ idom(b)
                dominance_frontier(runner) := dominance_frontier(runner) ∪ { b }
                runner := idom(runner)

위 코드에서 idom(b)는 b의 직접 지배자(immediate dominator)로, b를 엄격히 지배하지만 b를 엄격히 지배하는 다른 어떤 노드도 엄격히 지배하지 않는 유일한 노드이다.

Φ 함수의 수를 줄이는 변형

"최소" SSA는 각 이름이 정확히 한 번 값을 할당받고, 원래 프로그램에서 이름의 각 참조(사용)가 여전히 고유한 이름을 참조할 수 있도록 하는 데 필요한 최소한의 Φ 함수를 삽입한다. (후자의 요구 사항은 컴파일러가 각 연산에서 각 피연산자에 대한 이름을 기록할 수 있도록 하는 데 필요하다.)

그러나 이러한 Φ 함수 중 일부는 죽은 코드일 수 있다. 이러한 이유로 최소 SSA가 특정 절차에 필요한 가장 적은 수의 Φ 함수를 생성하는 것은 아니다. 일부 유형의 분석에서는 이러한 Φ 함수가 불필요하며 분석을 덜 효율적으로 실행시킬 수 있다.

가지치기된 SSA

가지치기된 SSA 형식은 간단한 관찰에 기반한다. Φ 함수는 Φ 함수 후에 "활성화"(live)된 변수에만 필요하다. (여기서 "활성화"는 값이 문제의 Φ 함수에서 시작하는 특정 경로를 따라 사용된다는 의미이다.) 변수가 활성화되어 있지 않으면 Φ 함수의 결과는 사용될 수 없으며 Φ 함수에 의한 할당은 죽은 코드이다.

가지치기된 SSA 형식을 구성할 때는 Φ 함수 삽입 단계에서 활성 변수 정보를 사용하여 주어진 Φ 함수가 필요한지 여부를 결정한다. 원래 변수 이름이 Φ 함수 삽입 지점에서 활성화되어 있지 않으면 Φ 함수는 삽입되지 않는다.

가지치기를 데드 코드 제거 문제로 취급하는 또 다른 가능성도 있다. 이 경우 Φ 함수는 입력 프로그램의 모든 사용이 해당 함수로 다시 작성되거나, 다른 Φ 함수의 인수로 사용될 경우에만 활성화된다. SSA 형식으로 들어갈 때 각 사용은 해당 사용을 지배하는 가장 가까운 정의로 다시 작성된다. 그런 다음 Φ 함수는 적어도 하나의 사용을 지배하는 가장 가까운 정의이거나, 활성 Φ 함수의 적어도 하나의 인수일 경우 활성으로 간주된다.

부분적으로 가지치기된 SSA

부분적으로 가지치기된 SSA 형식^[12]은 활성 변수 정보를 계산하는 상대적으로 높은 비용을 들이지 않고 Φ 함수의 수를 줄이려는 시도이다. 이 형식은 다음과 같은 관찰을 기반으로 한다. 변수가 기본 블록에 진입할 때 활성화되지 않으면 Φ 함수가 필요하지 않다. SSA 구성 중에 "블록 로컬" 변수에 대한 Φ 함수는 생략된다.

블록 로컬 변수 집합을 계산하는 것은 전체 활성 변수 분석보다 간단하고 빠른 절차이므로, 부분적으로 가지치기된 SSA 형식을 계산하는 것이 가지치기된 SSA 형식보다 효율적이다. 반면에 부분적으로 가지치기된 SSA 형식은 더 많은 Φ 함수를 포함하게 된다.

블록 인수

블록 인수는 Φ 함수의 대안이며 표현상 동일하지만 실제로는 최적화 과정에서 더 편리할 수 있다. 블록은 이름이 지정되고 함수 매개변수처럼 표기되는 블록 인수 목록을 취한다. 블록을 호출할 때 블록 인수는 지정된 값에 바인딩된다. MLton, 스위프트 SIL, LLVM MLIR은 블록 인수를 사용한다.^[13]

SSA 형식에서 벗어나기

SSA 형식은 일반적으로 직접 실행에 사용되지 않으며(SSA를 해석하는 것이 가능하긴 하지만^[14]), 종종 직접적으로 대응하는 다른 IR "위에" 사용된다. 이는 기존 IR의 부분(기본 블록, 명령어, 피연산자 등)과 SSA 대응 부분 사이를 매핑하는 일련의 함수로 SSA를 "구성"함으로써 달성할 수 있다. SSA 형식이 더 이상 필요 없을 때, 이러한 매핑 함수는 버려져서 이제 최적화된 IR만 남게 된다.

SSA 형식에서 최적화를 수행하면 일반적으로 얽힌 SSA 웹이 발생하며, 이는 피연산자가 모두 동일한 루트 피연산자를 갖지 않는 Φ 명령어가 있음을 의미한다. 이러한 경우 컬러아웃(color-out) 알고리즘이 SSA에서 벗어나기 위해 사용된다. 순진한 알고리즘은 Φ에 다른 루트 심볼의 소스를 놓는 각 선행 경로를 따라 복사본을 도입한다. 복사본을 적게 사용하여 SSA에서 벗어나는 여러 알고리즘이 있으며, 대부분은 간섭 그래프 또는 그 근사치를 사용하여 복사본 병합을 수행한다.^[15]

확장

SSA 형식에 대한 확장은 두 가지 범주로 나눌 수 있다.

이름 변경 방식 확장은 이름 변경 기준을 변경한다. SSA 형식은 값이 할당될 때마다 각 변수의 이름을 변경한다. 대안적인 방식으로는 정적 단일 사용 형식(각 변수가 사용될 때마다 각 문에서 이름을 변경함)과 정적 단일 정보 형식(각 변수가 값이 할당될 때마다, 그리고 후지배 프론티어에서 이름을 변경함)이 있다.

기능별 확장은 변수의 단일 할당 속성을 유지하면서 추가 기능을 모델링하기 위한 새로운 의미론을 통합한다. 일부 기능별 확장은 배열, 객체 및 별칭 포인터와 같은 고수준 프로그래밍 언어 기능을 모델링한다. 다른 기능별 확장은 투기와 예측과 같은 저수준 아키텍처 기능을 모델링한다.

SSA 형식을 사용하는 컴파일러

오픈 소스

• 모노는 미니라고 불리는 JIT 컴파일러에서 SSA를 사용한다.
• 웹킷은 JIT 컴파일러에서 SSA를 사용한다.^[16][17]
• 스위프트는 LLVM IR 위에 SIL(Swift Intermediate Language)이라는 자체 SSA 형식을 정의한다.^[18][19]
• 얼랭 컴파일러는 OTP 22.0에서 "정적 단일 할당(SSA)을 기반으로 한 중간 표현을 내부적으로 사용"하도록 재작성되었으며, 향후 릴리스에서 SSA를 기반으로 한 추가 최적화가 계획되어 있다.^[20]
• LLVM 컴파일러 인프라는 기본 코드 표현에서 모든 스칼라 레지스터 값(메모리를 제외한 모든 것)에 대해 SSA 형식을 사용한다. SSA 형식은 컴파일 과정 후반(종종 링크 타임에) 레지스터 할당이 발생할 때만 제거된다.
• GNU 컴파일러 모음 (GCC)은 버전 4 (2005년 4월 출시)부터 SSA를 광범위하게 사용한다. 프론트엔드는 "GENERIC" 코드를 생성하며, 이는 "gimplifier"에 의해 "GIMPLE" 코드로 변환된다. 그런 다음 "GIMPLE"의 SSA 형식에 고수준 최적화가 적용된다. 결과적으로 최적화된 중간 코드는 RTL로 번역되며, 여기서 저수준 최적화가 적용된다. 아키텍처별 백엔드는 마지막으로 RTL을 어셈블리어로 변환한다.
• Go (1.7: x86-64 아키텍처만 해당; 1.8: 지원되는 모든 아키텍처).^[21][22]
• IBM의 오픈 소스 적응형 자바 가상 머신, Jikes RVM은 SSA의 확장인 Extended Array SSA를 사용한다. 이는 스칼라, 배열, 객체 필드를 통합된 프레임워크에서 분석할 수 있게 해준다. Extended Array SSA 분석은 최대 최적화 수준에서만 활성화되며, 이는 가장 자주 실행되는 코드 부분에 적용된다.
• 모질라 모질라 파이어폭스 스파이더몽키 자바스크립트 엔진은 SSA 기반 IR을 사용한다.^[23]
• 크로미엄 V8 자바스크립트 엔진은 2010년 12월에 발표된 대로 Crankshaft 컴파일러 인프라에 SSA를 구현한다. 발표됨
• PyPy는 JIT 컴파일러에서 트레이스를 위한 선형 SSA 표현을 사용한다.
• 안드로이드 런타임^[24] 및 달빅 가상 머신은 SSA를 사용한다.^[25]
• 스탠다드 ML 컴파일러 MLton은 중간 언어 중 하나로 SSA를 사용한다.
• LuaJIT은 SSA 기반 최적화를 많이 사용한다.^[26]
• PHP 및 핵 컴파일러 HHVM은 IR에서 SSA를 사용한다.^[27]
• OCaml 컴파일러는 CMM IR(C--의 약자)에서 SSA를 사용한다.^[28]
• libFirm은 컴파일러의 중간 및 백엔드로 사용되는 라이브러리이며, SSA를 인식하는 레지스터 할당기를 사용하여 코드 생성 전까지 모든 스칼라 레지스터 값에 대해 SSA 형식을 사용한다.^[29]
• NIR을 통한 다양한 메사 드라이버, 셰이딩 언어를 위한 SSA 표현.^[30]

상업용

• 오라클의 핫스팟 자바 가상 머신은 JIT 컴파일러에서 SSA 기반 중간 언어를 사용한다.^[31]
• 마이크로소프트 Visual C++ 컴파일러 백엔드(Visual Studio 2015 Update 3에서 사용 가능)는 SSA를 사용한다.^[32]
• 벌칸 그래픽스 API 및 커널 언어인 OpenCL 컴퓨트 API를 위한 셰이딩 언어 표준인 SPIR-V는 SSA 표현이다.^[33]
• C, C++ 및 Fortran을 포함하는 IBM XL 컴파일러 제품군.^[34]
• CUDA^[35]

연구 및 폐기

• ETH Oberon-2 컴파일러는 SSA의 변형인 "GSA"를 통합한 최초의 공개 프로젝트 중 하나였다.
• Open64 컴파일러는 전역 스칼라 최적화 프로그램에서 SSA 형식을 사용했지만, 코드는 SSA 형식으로 변환된 후 다시 SSA 형식에서 벗어났다. Open64는 SSA 형식의 확장을 사용하여 스칼라 값뿐만 아니라 메모리도 SSA 형식으로 표현한다.
• 2002년, 연구원들은 IBM의 JikesRVM(당시 Jalapeño라고 불림)을 수정하여 표준 자바 바이트코드와 타입 안전 SSA(SafeTSA) 바이트코드 클래스 파일을 모두 실행하도록 했고, SSA 바이트코드를 사용하는 것이 상당한 성능 향상을 가져온다는 것을 입증했다.
• jackcc는 학술 명령어 집합 Jackal 3.0용 오픈 소스 컴파일러이다. 이 컴파일러는 중간 표현을 위해 SSA와 함께 간단한 3-피연산자 코드를 사용한다. 흥미로운 변형으로, Φ 함수를 소위 SAME 명령어로 대체하는데, 이는 레지스터 할당기에게 두 개의 활성 범위(live range)를 동일한 물리적 레지스터에 배치하도록 지시한다.
• 1994년경 일리노이 콘서트 컴파일러(Illinois Concert Compiler)^[36]는 SSU(Static Single Use)라는 SSA 변형을 사용했는데, 이는 각 변수에 값이 할당될 때마다 그리고 해당 변수가 사용되는 각 조건부 문맥에서 이름을 변경한다. 이는 본질적으로 위에서 언급된 정적 단일 정보 형식이다. SSU 형식은 존 플레비악(John Plevyak)의 박사 논문에 문서화되어 있다.
• COINS 컴파일러는 여기에서 설명된 바와 같이 SSA 형식 최적화를 사용한다.
• 리저버 랩스(Reservoir Labs)의 R-스트림(R-Stream) 컴파일러는 비-SSA(쿼드 리스트), SSA 및 SSI(Static Single Information^[37]) 형식을 지원한다.^[38]
• 컴파일러는 아니지만, Boomerang 디컴파일러는 내부 표현에 SSA 형식을 사용한다. SSA는 표현 전파, 매개변수 및 반환 식별, 보존 분석 등을 단순화하는 데 사용된다.
• DotGNU Portable.NET은 JIT 컴파일러에서 SSA를 사용했다.