Описна статистика - Типови податоци

Номинални податоци

Тука обележијето е чисто квалитативно. Можните исходи се зборови-имиња и истите се самите категории, односно класи при групирање.  Со вакви податоци не можеме да правиме никакви математички операции.

Важно: Номинални податоци секогаш се групираат.

---

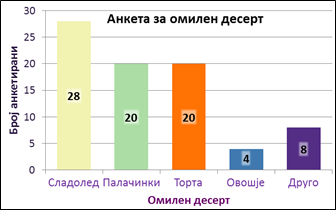
Пример Д-1: Анкетирани се 80 луѓе за нивниот омилен десерт (види Табела 17).

Анкета „Кој ти е омилен десерт?“ С С Д П Т С С Д Т П Т Д П С С С П О О Д П П О С С П Т С П Т Т Т С Т С С Т П П П Т Т С С С П Т Т С Т П Д С П С С С Т П Т Т Т С С Т С Т С П П Д С Д О Д П С П С П

Легенда C=Сладолед П=Палачинки Т=Торта О=Овошје Д=Друго

Табела 17: Резултати од анкета

Решение: Обележјето е „омилен десерт“ и можните исходи тука се {С, П, Т, О, Д}, односно {Сладолед, Палачинки, Торта, Овошје, Друго}.  Јасно е дека се имиња. Тие се и самите класи при групирање.  Значи, податоците се номинални и треба да се групираат по класи = имиња на десерт. Ја најдеме честотата на секој тип на десерт (проверувајќи дека честотите се собираат до N=80). Во Табела 18 е соодветната честотна табела.

Класа	Сладолед	Палачинки	Торта	Овошје	Друго	Проверка
Честота f	28	20	20	4	8	Σf=80=N

Табела 18: Номинални податоци – организирани за обработка во честотна табела

Ги претставиме овие податоци со столбест дијаграм (види Слика 13).

Слика 13: Столбест дијаграм за анкетата за омилен десерт

Класите тука се имиња и не може математички да се работат ништо со нив. Меѓутоа, честотите се броеви и може да се пресмета процентот кој припаѓа во секоја класа, односно да се преметат т.н. релативни честоти.

---

Релативна честота = процент = f/N

Ја делиме честотата со вкупниот број на честотите, т.е. со големината на податоци N. Потоа, овој резултат го помножиме со 100% за да добиме процент.

---

Во пример Д-1, вкупниот број на честотите е N=80. Ја делиме секоја честота со N=80 за да ја добиеме релативна честотна табела (види Табела 19 ).
Симболот за честота е f, а симболот за релативна честота е f/N.

Класа	честота f	Релативна честота f/N(број)	Релативна честота f/N %
Сладолед	28	28⁄80=0.35	0.35•100%=35%
Палачинки	20	20⁄80=0.25	0.25•100%=25%
Торта	20	22⁄80=0.25	0.25•100%=25%
Овошје	4	2⁄80=0.05	0.05•100%=5%
Друго	8	8⁄80=0.1	0.1•100%=10%
Проверка	Σf=80=N	Σf/N =1	Σf/N =100%

Табела 19: Релативна честотна табела

Релативна честотна табела може графички да се претстави со столбест или со секторски дијаграм како во Слика 16 и Слика 17. Забележете ги разликите помеѓу двата столбест дијаграми Слика 13 и Слика 16.  Секторски дијаграм секогаш е релативна!

Слика 14: Столбест дијаграм со релативни честоти

Слика 15: Секторски дијаграм