Тороид

Во математиката, тороид е површина на револуција со дупка во средината. Оската на вртење минува низ дупката и така не ја пресекува површината.^[1] На пример, кога правоаголникот се врти околу оската напоредна на еден од неговите рабови, тогаш се создава шуплив прстен со пресек на правоаголник. Ако се врти фигурата е круг, тогаш предметот е наречен тор.

Тороид кој користи квадрат.

Торот е еден вид тороид.

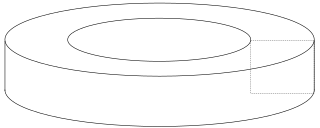
Поимот тороид е користен и за опишување на тороидален полиедар. Во овој контекст, тороидот не мора да биде кружен и може да има кој било број на дупки. Тороид со дупка како „g“ може да биде гледан како приближување на површината на тор со тополошки род, „g“, од 1 или поголем. Ојлеровата одлика χ на тороидот со g дупка е 2(1- g ).^[2]

Торот е пример за тороид, кој е површина на крофна. Крофните се пример за цврст тор создаден со вртење на дискот и не треба да бидат мешани со тороиди.

Тороидалните структури се јавуваат и во природни и во синтетички материјали.^[3]

Равенки

Тороидот е одредуван со радиусот на вртење R измерен од средината на вртливиот дел. За симетрични пресеци може да бидат пресметани волуменот и површината на телото (со обем C и плоштина А на делот):

Квадратен тороид

Волуменот (V) и површината (S) на тороид се дадени со следните равенки, каде што A е плоштината на квадратниот пресек на страната, а R е радиусот на вртење.

${\displaystyle V=2\pi RA}$

${\displaystyle S=2\pi RC}$

Кружен тороид

Волуменот (V) и површината (S) на тороид се дадени со следните равенки, каде што r е радиусот на кружниот пресек, а R е радиусот на целокупниот облик.

${\displaystyle V=2\pi ^{2}r^{2}R}$

${\displaystyle S=4\pi ^{2}rR}$

Поврзано

• Тороидни индуктори и трансформатори
• Тороидни пропелери
• Анулус
• Соленоид
• Хеликс