സമഭുജത്രികോണം

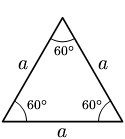
മൂന്നു വശങ്ങളും മൂന്നു കോണളവുകളും തുല്യമായ ത്രികോണങ്ങളാണ് സമഭുജ ത്രികോണങ്ങൾ. ആയതിനാൽ ഓരോ കോണളവും 60 ഡിഗ്രീ വീതമായിരിയ്ക്കും.

സമഭുജത്രികോണം

സമഭുജത്രികോണം

സമഭുജ ത്രികോണം

ഒരു വശം ${\displaystyle a\,}$യും ലംബശീർ‌ഷം ${\displaystyle h\,}$ഉം തന്നിരുന്നാൽ സമഭുജത്രികോണത്തിന്റെ വിസ്തീർ‌ണ്ണം കാണുന്നതിന് ${\displaystyle {\frac {1}{2}}ah\,}$ എന്ന സൂത്രവാക്യം ഉപയോഗിയ്ക്കുന്നു.

${\displaystyle a\,}$ വശമായുള്ള സമഭുജത്രികോണം ആധാരമാക്കി വരയ്ക്കുന്ന:

• ${\displaystyle r\,}$ ആരമായുള്ള അന്തർ‌വൃത്തത്തിന്റെ വിസ്തീർ‌ണ്ണം ${\displaystyle \pi r^{2}\,}$ അഥവാ ${\displaystyle {\frac {1}{12}}\pi a^{2}\,}$ എന്ന സൂത്രവാക്യം ഉപയോഗിച്ചും
• ${\displaystyle R\,}$ ആരമായുള്ള പരിവൃത്തത്തിന്റെ വിസ്തീർ‌ണ്ണം ${\displaystyle \pi R^{2}\,}$ അഥവാ ${\displaystyle {\frac {1}{3}}\pi a^{2}}$ എന്ന സൂത്രവാക്യം ഉപയോഗിച്ചും കണ്ടെത്താം.
• സമഭുജതികോണത്തിന്റെ തുല്യ വശങ്ങളെ aഎന്നു അടയാളപ്പെടുത്തിയാൽ, പൈത്ഗോറസ് തത്ത്വം ഉപ്യോഗിച്ച്,
  • വിസ്തീർണ്ണം ${\displaystyle A={\frac {\sqrt {3}}{4}}a^{2}}$

• • ചുറ്റളവ് ${\displaystyle p=3a\,\!}$

• • പരിവൃത്തത്തിന്റെ ആരം ${\displaystyle R={\frac {a}{\sqrt {3}}}}$
  • ആന്തരവൃത്തത്തിന്റെ ആരം ${\displaystyle r={\frac {\sqrt {3}}{6}}a}$ or ${\displaystyle r={\frac {R}{2}}}$

• • പരിവൃത്തത്തിന്റെ കേന്ദ്രവും ആന്തര വൃത്തത്തിന്റെ കേന്ദ്രവും ത്രികോണത്തിന്റെ ജ്യാമിതീയ കേന്ദ്രവും ഒന്നു തന്നെ ആയിരിക്കും. 

• • ഏതു വശത്തു നിന്നുമുള്ള ഉയരം, ${\displaystyle h={\frac {\sqrt {3}}{2}}a}$.  പരിവൃത്തത്തിന്റെ ആരം R, ആണെങ്കിൽത്രികോണമിതി ഉപയോഗിച്ച്,
  • ത്രികോണത്തിന്റെ വിസ്തീർണ്ണം ${\displaystyle \mathrm {A} ={\frac {3{\sqrt {3}}}{4}}R^{2}}$ പല പരിമാണങ്ങൾക്കും ശീർഷത്തിൽ നിന്നും എതിർവാശത്തേക്കുള്ള ഉന്നതി ("h") ന് ബന്ധങ്ങളുണ്ട്:
  • വിസ്തീർണ്ണം   ${\displaystyle A={\frac {h^{2}}{\sqrt {3}}}}$

• • ഓരോ വശത്തുനിന്നും കേന്ദ്രത്തിലേക്കുള്ള അകലം  ${\displaystyle {\frac {h}{3}}}$

• • പരിവൃത്തത്തിന്റെ ആരം  ${\displaystyle R={\frac {2h}{3}}}$

• • ആന്ത്ര വൃത്തത്തിന്റെ ആരം  ${\displaystyle r={\frac {h}{3}}}$  ഒരു സമഭുജ ത്രികോണത്തിൽ, ഉന്നതി, കോണിന്റെ സമഭാജികൾ, ലംബസമഭാജികൾ, മാധ്യമം എന്നിവ ഒന്നായിരിക്കും.
• == സവിശേഷതകൾ == ABC എന്ന ത്രികോണത്തിന്റെ വശങ്ങൾ a, b, c, അർദ്ധചുറ്റളവ് s, വിസ്തീർണ്ണം T, പരിവൃത്തത്തിന്റെ ആരങ്ങൾ r_a, r_b, r_c (തൊടുവര യഥാക്രമം a, b, c ), പരിവൃത്തത്തിൻടേയും ആന്ത്രവൃത്തത്തിൻടേയും ആരങ്ങൾ യഥാക്രമം R and rആവുംപ്പോൾ, സമഭുജമാവണമെങ്കിൽ താഴെ പറയുന്ന ഒമ്പത് ഇനങ്ങളിൽ ഒന്നെങ്കിലും ശരിയാവണം. ഈ വിശേഷതകൾ സമഭുജത്രികോണത്തിന്റെ മാത്രം പ്രത്യേകതയാണ്. 

നിർ‌മ്മിതി

സമഭുജ ത്രികോണത്തിന്റെ നിർമ്മിതി

ആരമായുള്ള ഒരു വൃത്തം നിർ‌മിയ്ക്കുക. ഇതേ ആരത്തിൽ തന്നെ കോം‌പസ്സുപയോഗിച്ച് വേറൊരു വൃത്തം നിർമ്മിച്ച്, വൃത്തകേന്ദ്രങ്ങളേയും വൃത്തങ്ങൾ തമ്മിൽ സന്ധിയ്ക്കുന്ന ബിന്ദുക്കളേയും യോജിപ്പിച്ചാൽ സമഭുജത്രികോണം ലഭിയ്ക്കും.