മാട്രിക്സ്
From Wikipedia, the free encyclopedia
Remove ads
ഗണിതശാസ്ത്രത്തിൽ ചതുരാകൃതിയിൽ സംഖ്യകളെ വിന്യസിക്കുന്ന രീതിയാണ് മാട്രിക്സ്.സംഖ്യകളെ വരികളും നിരകളും ആയാണ് വിന്യസിക്കുന്നത്.നിരകളുടേയും വരികളുടേയും എണ്ണം തുല്യമാവണമെന്നില്ല.ഒരു മട്രിക്സിന് സാരണികത്തെപ്പോലെ(Determinent) സംഖ്യാത്മകമൂല്യം കണ്ടെത്താനാവില്ല.സംഖ്യകളെ മൊത്തത്തിൽ ബ്രാക്കറ്റിനുള്ളിലായാണ് വിന്യസിക്കുന്നത്.
കോടി
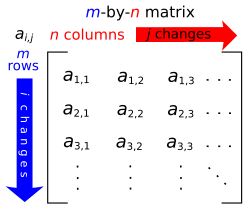
ഒരു മാട്രിക്സിന്റെ കോടി(Order) നിർണ്ണയിക്കുന്നത് അതിന്റെ നിരയേയും വരിയേയും അടിസ്ഥാനപ്പെടുത്തിയാണ്.ഒരു മാട്രിക്സിലെ വരികളുടേയും നിരകളുടേയും എണ്ണത്തേയാണ് കോടി എന്നു പറയുന്നത്.m അക്ഷരം വരിയുടെ എണ്ണത്തേയും n എന്ന അക്ഷരം നിരയുടെ എണ്ണത്തേയും സൂചിപ്പിച്ചാൽ കോടി mXn (m ബൈ n) ആണെന്ന് പറയാം.
വിവിധതരം മാട്രിക്സുകൾ
നിര മട്രിക്സ്
ഒരു നിര മാത്രമുള്ള മാട്രിക്സാണ് നിര മാട്രിക്സ്(row matrix)
വരി മാട്രിക്സ്
ഒരു വരി മാത്രമുള്ള മാട്രിക്സാണ് വരി മാട്രിക്സ്(column matrix)
സമചതുര മാട്രിക്സ്
ഒരു മാട്രിക്സിന്റെ നിരയുടെ എണ്ണവും വരിയുടെ എണ്ണവും തുല്യമായാൽ അത്തരം മാട്രിക്സാണ് സമചതുരമാട്രിക്സ്(Square matrix).ഇവിടെ m=n ആയിരിയ്ക്കും
വികർണ്ണ മാട്രിക്സ്
വികർണ്ണപദങ്ങളൊഴികെ എല്ലാപദങ്ങളും പൂജ്യം ആയ മാട്രിക്സ് ആണ് വികർണ്ണമാട്രിക്സ്(Diagonal matrix).ഇത് ഒരു സമചതുരമാട്രിക്സ് ആയിരിയ്ക്കുക കൂടി വേണം.
തൽസമക മാട്രിക്സ്
ഒരു വികർണ്ണമാട്രിക്സിലെ വികർണ്ണങ്ങളെല്ലാം 1ഉം ബക്കിയെല്ലാം പൂജ്യവും ആയ മാട്രിക്സ് ആണിത്(Identity matrix).ഇതിനെ യൂണിറ്റ് മാട്രിക്സ് എന്നുകൂടി പറയുന്നു.
Remove ads
പക്ഷാന്തരിതം
ഒരു മാട്രിക്സിലെ വരികളെ നിരകളായും നിരകളെ വരികളായും മാറ്റിയെഴുതുമ്പോൾ കിട്ടുന്ന പുതിയ മാട്രിക്സ് ആണ് പക്ഷാന്തരിതം(Transpose).mXn കോടിയുള്ള ഒരു മാട്രിക്സിന്റെ പക്ഷാന്തരിതത്തിന്റെ കോടി nXm ആയിരിക്കും.
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads
