ഋണസംഖ്യ
From Wikipedia, the free encyclopedia
Remove ads
പൂജ്യത്തിൽ കുറവായ വാസ്തവികസംഖ്യകളെ ഋണസംഖ്യ എന്ന് പറയുന്നു.നഷ്ടത്തിന്റെയോ അസാന്നിദ്ധ്യത്തിന്റെയോ അളവ് സൂചിപ്പിക്കാനാണ് ഇവ മിക്കപ്പോഴും ഉപയോഗിക്കുന്നത്. ഉദാഹരണത്തിന് കടത്തെ ഋണസംഖ്യയാൽ കുറിക്കുന്ന മുതലായി കണക്കാക്കാം,എന്തിന്റെയെങ്കിലും അളവിലുണ്ടാകുന്ന കുറവിനെ ഋണസംഖ്യകൊണ്ട് കുറിക്കുന്ന വർദ്ധനയായി കണക്കാക്കാം. ഋണസംഖ്യയാണെന്ന് സൂചിപ്പിക്കാൻ സംഖ്യക്കു മുൻപിൽ ഒരു ഋണ ചിഹ്നം ഇടുന്നു. ഉദാ -128. പൂജ്യം ഒരു ഋണസംഖ്യയോ ധനസംഖ്യയോ അല്ല. താഴെക്കാണുന്ന വാസ്തവികസംഖ്യരേഖ ഋണസംഖ്യ, പൂജ്യം, ധനസംഖ്യ എന്നിവ തമ്മിലുള്ള ബന്ധത്തെ കാണിക്കുന്നു.
ചൈനയിലെ ഹാൻ രാജവംശത്തിന്റെ കാലത്ത് (ബി.സി.ഇ 202 - സി.ഇ 220)എഴുതപ്പെട്ട 'ഗണിതശാസ്ത്ര കലയെക്കുറിച്ചുള്ള ഒമ്പത് അധ്യായങ്ങളിൽ' നെഗറ്റീവ് സംഖ്യകൾ ഉപയോഗിച്ചിട്ടുണ്ട്.[1] ലിയു ഹുയി (ഏകദേശം മൂന്നാം നൂറ്റാണ്ട്) നെഗറ്റീവ് സംഖ്യകൾ കൂട്ടുന്നതിനും കുറയ്ക്കുന്നതിനുമുള്ള നിയമങ്ങൾ പ്രമാണീകരിച്ചു.[2] ഏഴാം നൂറ്റാണ്ടോടെ, ബ്രഹ്മഗുപ്തനെപ്പോലുള്ള ഇന്ത്യൻ ഗണിതശാസ്ത്രജ്ഞർ നെഗറ്റീവ് സംഖ്യകളുടെ ഉപയോഗം വിവരിച്ചു. ഇസ്ലാമിക ഗണിതശാസ്ത്രജ്ഞർ നെഗറ്റീവ് സംഖ്യകൾ കുറയ്ക്കുന്നതിനും ഗുണിക്കുന്നതിനുമുള്ള നിയമങ്ങൾ വികസിപ്പിക്കുകയും നെഗറ്റീവ് ഗുണകങ്ങളുള്ള ഗണിതപ്രശ്നങ്ങൾക്ക് ഉത്തരം കണ്ടെത്തുകയും ചെയ്തു.[3]
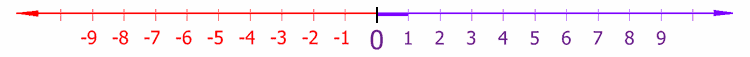
Remove ads
ഋണസംഖ്യയുടെ സ്വഭാവഗുണങ്ങൾ (properties of negative numbers)
- ഒരു സംഖ്യയിൽ നിന്ന് ഒരു ഋണസംഖ്യ വ്യവകലനം ചെയ്യുമ്പോൾ അത് ഫലത്തിൽ സങ്കലനമാവുന്നു ഉദാ : (+8) - (-2) = (+10).
- ഒരു ഋണസംഖ്യയും ധനസംഖ്യയുമായുള്ള ഗുണിക്കുമ്പോൾ കിട്ടുന്നഫലം ഋണസംഖ്യയായിരിക്കും ഉദാ : (+8) x (-2) = (-16)
- ഋണസംഖ്യകൾ മറ്റൊരു സംഖ്യയുമായി ഹരണം ചെയ്യുമ്പോൾ ഫലം ഋണമായിരിക്കും ഉദാ : (+8) ÷ (-2) = (-4)
അവലംബം
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads