ਗੁਣਕ ਪ੍ਰਬੰਧ
From Wikipedia, the free encyclopedia
Remove ads
ਰੇਖਾ-ਗਣਿਤ ਵਿੱਚ, ਗੁਣਕ ਪ੍ਰਬੰਧ ਜਾਂ ਕੋਆਰਡੀਨੇਟ ਸਿਸਟਮ ਉਹ ਪ੍ਰਬੰਧ ਹੁੰਦਾ ਹੈ ਜੋ ਕਿਸੇ ਬਿੰਦੂ ਜਾਂ ਹੋਰ ਰੇਖਕੀ ਅੰਸ਼ ਦੀ ਸਥਿਤੀ ਮਾਪਣ ਲਈ ਇੱਕ ਜਾਂ ਜ਼ਿਆਦਾ ਅੰਕ ਜਾਂ ਗੁਣਕ ਵਰਤਦਾ ਹੈ।[1][2] ਇਹਨਾਂ ਗੁਣਕਾਂ ਦੀ ਤਰਤੀਬ ਬਹੁਤ ਜ਼ਰੂਰੀ ਹੈ ਅਤੇ ਇਹ ਕਈ ਵਾਰ ਤਰਤੀਬੀ ਤਿਗੜੀ ਵਿੱਚ ਆਪਣੀ ਸਥਿਤੀ ਤੋਂ ਜਾਂ ਕਈ ਵਾਰ ਇੱਕ ਅੱਖਰ, ਜਿਵੇਂ ਕਿ x-ਗੁਣਕ, ਤੋਂ ਜਾਣੇ ਜਾਂਦੇ ਹਨ। ਇਹ ਗੁਣਕ ਮੁੱਢਲੇ ਗਣਿਤ ਵਿੱਚ ਹਕੀਕੀ (ਰੀਅਲ) ਮੰਨੇ ਜਾਂਦੇ ਹਨ ਪਰ ਅਮੂਰਤ ਪ੍ਰਬੰਧਾਂ ਵਿੱਚ ਬੇਹਕੀਕੀ (ਕੰਪਲੈਕਸ) ਵੀ ਹੋ ਸਕਦੇ ਹਨ। ਇਸ ਗੁਣਕ ਪ੍ਰਬੰਧ ਦੀ ਵਰਤੋਂ ਨਾਲ਼ ਜਿਆਮਤੀ ਦੇ ਪ੍ਰਸ਼ਨਾਂ ਨੂੰ ਅੰਕ-ਸੰਬੰਧੀ ਸੁਆਲਾਂ ਵਿੱਚ ਬਦਲਿਆ ਜਾਂ ਸਕਦਾ ਹੈ ਜਾਂ ਇਸ ਦੇ ਉਲਟ ਵੀ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ; ਇਹ ਵਿਸ਼ਲੇਸ਼ਣੀ ਰੇਖਾ-ਗਣਿਤ ਦਾ ਅਧਾਰ ਹੈ।[3]
Remove ads
ਗਿਣਤੀ ਰੇਖਾ
ਕਿਸੇ ਗੁਣਕ ਪ੍ਰਬੰਧ ਦੀ ਸਭ ਤੋਂ ਸਰਲ ਮਿਸਾਲ ਹੈ ਗਿਣਤੀ ਰੇਖਾ ਰਾਹੀਂ ਕਿਸੇ ਰੇਖਾ ਉੱਤੇ ਹਕੀਕੀ ਅੰਕਾਂ ਦੀ ਮਦਦ ਨਾਲ਼ ਬਿੰਦੂ ਦਾ ਪਤਾ ਲਾਉਣਾ। ਇਸ ਪ੍ਰਬੰਧ ਵਿੱਚ ਇੱਕ ਮਨ ਮੰਨਿਆ ਬਿੰਦੂ O (ਓਰਿਜਿਨ ਜਾਂ ਸਰੋਤ ਬਿੰਦੂ) ਦਿੱਤੀ ਗਈ ਰੇਖਾ ਉੱਤੇ ਚੁਣ ਲਿਆ ਜਾਂਦਾ ਹੈ। ਬਿੰਦੂ P ਦਾ ਗੁਣਕ O ਤੋਂ P ਤੱਕ ਦੇ ਨਿਸ਼ਾਨ ਸਮੇਤ ਫ਼ਾਸਲੇ ਨੂੰ ਕਿਹਾ ਜਾਂਦ ਹੈ ਜਿਸ ਵਿੱਚ ਨਿਸ਼ਾਨਯੁਕਤ ਫ਼ਾਸਲੇ ਦਾ ਭਾਵ ਹੈ ਕਿ ਉਹ ਫ਼ਾਸਲਾ ਜੋ P ਦੇ ਰੇਖਾ ਉਤਲੇ ਪਾਸੇ ਮੁਤਾਬਕ ਪਾਜ਼ਟਿਵ ਜਾਂ ਰਿਣ ਰਾਸ (ਨੈਗਟਿਵ) ਹੋਵੇ। ਹਰੇਕ ਬਿੰਦੂ ਨੂੰ ਇੱਕ ਅਨੂਠਾ ਗੁਣਕ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ਅਤੇ ਹਰੇਕ ਹਕੀਕੀ ਅੰਕ ਕਿਸੇ ਅਨੂਠੇ ਬਿੰਦੂ ਦਾ ਗੁਣਕ ਹੁੰਦਾ ਹੈ।[4]
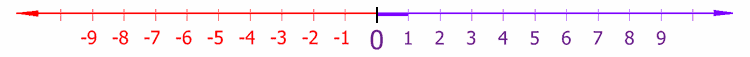
Remove ads
ਕਾਰਤੀਸੀ ਗੁਣਕ ਪ੍ਰਬੰਧ

ਗੁਣਕ ਪ੍ਰਬੰਧ ਦੀ ਇੱਕ ਮੂਲ ਰੂਪੀ ਮਿਸਾਲ ਕਾਰਤੀਸੀ ਗੁਣਕ ਪ੍ਰਬੰਧ ਹੈ। ਇੱਕ ਤਲ ਉੱਤੇ ਦੋ ਲੰਬ-ਰੂਪੀ ਰੇਖਾਵਾਂ ਚੁਣ ਲਈਆਂ ਜਾਂਦੀਆਂ ਹਨ ਅਤੇ ਕਿਸੇ ਬਿੰਦੂ ਦੇ ਗੁਣਕ ਇਹਨਾਂ ਰੇਖਾਵਾਂ ਤੋਂ ਉਸ ਦੇ ਨਿਸ਼ਾਨੀਦਾਰ ਫ਼ਾਸਲੇ ਲਏ ਜਾਂਦੇ ਹਨ।

ਤਿੰਨ ਆਯਾਮਾਂ ਵਿੱਚ ਤਿੰਨ ਲੰਬਮਾਪੀ ਰੇਖਾਵਾਂ ਲਈਆਂ ਜਾਂਦੀਆ ਹਨ ਅਤੇ ਬਿੰਦੂ ਦੇ ਤਿੰਨ ਗੁਣਕ ਹਰੇਕ ਤਲ ਤੋਂ ਬਿੰਦੂ ਦੇ ਨਿਸ਼ਾਨੀਯੁਕਤ ਫ਼ਾਸਲੇ ਹੁੰਦੇ ਹਨ। ਇਸੇ ਤਰ੍ਹਾਂ ਕਿਸੇ ਵੀ n-ਆਯਾਮੀ ਯੂਕਲਿਡੀ ਖ਼ਲਾਅ ਵਿੱਚ ਕਿਸੇ ਬਿੰਦੂ ਦੇ ਗੁਣਕ ਕੱਢੇ ਜਾ ਸਕਦੇ ਹਨ।
Remove ads
ਹਵਾਲੇ
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads