Koło (teoria grafów)

Koło – w teorii grafów, graf powstały z cyklu poprzez dodanie nowego wierzchołka połączonego krawędzią z każdym wierzchołkiem tego cyklu. Koło o ${\displaystyle n}$ wierzchołkach oznacza się symbolem ${\displaystyle W_{n}}$^[1].

Ten artykuł dotyczy klasy grafów. Zobacz też: inne znaczenia tego słowa.

Przykłady kół

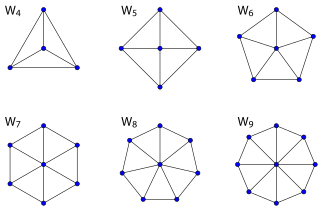
Koło o ${\displaystyle n}$ wierzchołkach jest grafem ostrosłupa o podstawie ${\displaystyle (n-1)}$-kąta^[2].

Graf ${\displaystyle W_{n}}$ ma ${\displaystyle n}$ wierzchołków i ${\displaystyle 2(n-1)}$ krawędzi. Koło o czterech wierzchołkach jest izomorficzne z grafem pełnym o tej samej liczbie wierzchołków. Z kolei ${\displaystyle W_{5}}$ jest izomorficzne z pełnym grafem trójdzielnym ${\displaystyle K_{1,2,2}}$^[2].

Własności

Koła o nieparzystej liczbie wierzchołków są 3-chromatyczne, a koła o parzystej liczbie wierzchołków mają liczbę chromatyczną równą 4^[1].

Wszystkie koła są planarne. Każde koło jest izomorficzne ze swoim grafem dualnym^[1].

Każde koło jest grafem hamiltonowskim. Co więcej, graf ${\displaystyle W_{n}}$ zawiera dokładnie ${\displaystyle n-1}$ cykli Hamiltona^[3].

Graf ${\displaystyle W_{7}}$ jest jedynym kołem, które można narysować na płaszczyźnie tak, aby każda krawędź była jednostkowej długości. Przy zachowaniu tej reguły, pozostałe koła można narysować w przestrzeni trójwymiarowej^[4].

Dla każdego ${\displaystyle k,}$ wszystkie grafy 3-spójne o odpowiednio wielu wierzchołkach zawierają ${\displaystyle W_{k}}$ lub ${\displaystyle K_{3,k}}$ jako minor^[5][6].