Półprosta

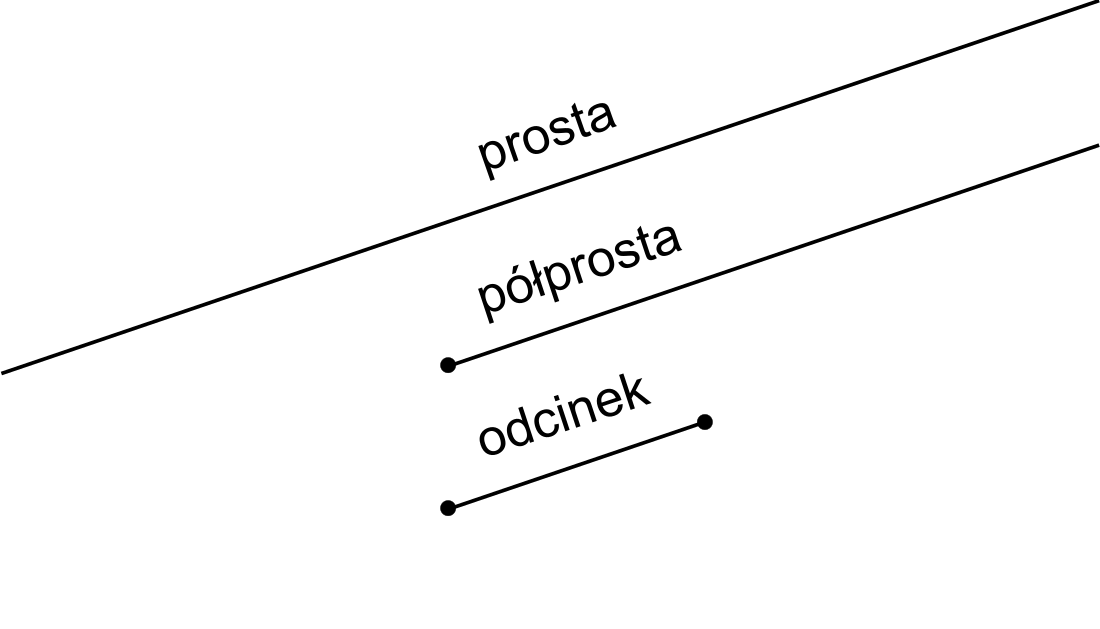
Półprosta – figura geometryczna składająca się z punktów prostej leżących po jednej stronie pewnego punktu tej prostej^[1]. Punkt ten jest nazywany początkiem półprostej^[a]. Bardzo często do tak określonej półprostej dołącza się początek półprostej – mówimy wówczas o półprostej domkniętej (z początkiem)^[2]. W przeciwnym wypadku mówimy o półprostej otwartej (bez początku).

Prosta, półprosta i odcinek. Dla prostej i półprostej widać tylko fragment mieszczący się na rysunku. Wypełnione kółeczka (tzw. nulki) symbolizują punkty na końcach odcinka i na początku półprostej, które także do odcinka i półprostej należą.

Półprostą o początku w punkcie ${\displaystyle A}$ i przechodzącą przez punkt ${\displaystyle B}$ oznaczamy jako półprostą ${\displaystyle AB.}$

Niekiedy półprostą nazywa się promieniem^[3]. Często wygodnie jest oznaczać przez ${\displaystyle A/B}$ promień otwarty wychodzący z punktu ${\displaystyle A}$ i nieprzechodzący przez punkt ${\displaystyle B}$^[4]. Inaczej mówiąc, promień ${\displaystyle A/B}$ składa się z tych punktów prostej ${\displaystyle AB,}$ które leżą po przeciwnej stronie punktu ${\displaystyle A}$ niż punkt ${\displaystyle B.}$

Inne definicje półprostej

• Półprostą (domkniętą) o początku w punkcie ${\displaystyle A}$ można też zdefiniować jako maksymalny podzbiór prostej przechodzącej przez punkt ${\displaystyle A,}$ taki że punkt ${\displaystyle A}$ należy do tego podzbioru, ale nie leży on między żadnymi dwoma innymi punktami tego podzbioru.
• Półprostą (domkniętą) ${\displaystyle AB}$ można również zdefiniować jako sumę mnogościową wszystkich odcinków o końcu w punkcie ${\displaystyle A}$ zawierających punkt ${\displaystyle B}$^[5].

Własności

• Zbiór rzędnych punktów danej półprostej jest albo zbiorem jednopunktowym (gdy półprosta jest zawarta w prostej prostopadłej do osi rzędnych), albo przedziałem nieskończonym. To samo można powiedzieć o zbiorze odciętych punktów półprostej^[b].
• Dla każdych dwóch różnych punktów ${\displaystyle A}$ i ${\displaystyle B}$ półproste ${\displaystyle A/B}$ i ${\displaystyle B/A}$ są rozłączne. Suma mnogościowa tych promieni i odcinka ${\displaystyle {\overline {AB}}}$ jest równa prostej ${\displaystyle AB{:}}$

${\displaystyle A/B\cup {\overline {AB}}\cup B/A={\text{prosta }}AB.}$

• Na zbiorze półprostych (promieni) zawartych w danej prostej można określić relację równoważności ${\displaystyle R_{k}.}$ Promienie ${\displaystyle p_{1}}$ i ${\displaystyle p_{2}}$ są w niej równoważne, jeśli jeden z nich jest zawarty w drugim:

${\displaystyle p_{1}R_{k}p_{2}\Leftrightarrow p_{1}\subset p_{2}\vee p_{2}\subset p_{1},}$

Relacja ta ma dwie klasy równoważności nazywane kierunkami promieni na tej prostej.

Zobacz też

Zobacz hasło półprosta w Wikisłowniku

• prosta
• odcinek
• kąt

Uwagi

1. Dwa punkty ${\displaystyle A}$ i ${\displaystyle B}$ prostej ${\displaystyle AB}$ leżą po jednej stronie punktu ${\displaystyle C}$ leżącego na tej prostej, jeśli punkt ${\displaystyle C}$ nie leży między tymi punktami, to znaczy nie zachodzi relacja ${\displaystyle [ACB]}$ z geometrii uporządkowania.
2. Własność nieprawdziwa w geometrii hiperbolicznej. W niej rzut półprostej może być odcinkiem.