Função racional

Em matemática, uma função racional é qualquer função que pode ser expressa como uma razão (quociente) de polinômios, i.e. uma fração algébrica^[1]. Para uma simples variável ${\displaystyle x}$, uma típica função racional é, portanto:^[2]

Gráfico de 1/x, um exemplo de função racional.

$${\displaystyle f(x)={\frac {P(x)}{Q(x)}}}$$

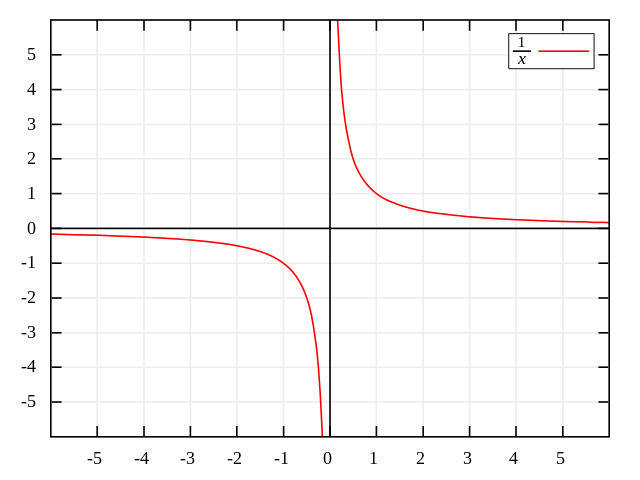
As funções racionais são classificadas em próprias, se o grau do polinômio do numerador for inferior ao grau do polinômio do denominador, e impróprias, se o grau do numerador for maior ou igual ao grau do denominador.

• Exemplos de funções racionais próprias:

${\displaystyle \left({\frac {4s-1}{s^{2}+s-2}}\right)}$

${\displaystyle \left({\frac {5x-7}{3x^{3}+2x-5}}\right)}$

• Exemplos de funções racionais impróprias:

${\displaystyle \left({\frac {2y^{3}-3y}{y^{2}-5y+6}}\right)}$

${\displaystyle \left({\frac {3s^{2}+4s-1}{s^{2}+s-2}}\right)}$^[3]

Assíntotas

Ver artigo principal: Assintota

Assíntotas verticais

O gráfico da função racional ${\displaystyle f(x)={\frac {P(x)}{Q(x)}}}$ terá uma assíntota vertical em ${\displaystyle x=a}$ se algum dos limites ${\displaystyle \lim _{x\to a^{\pm }}f(x)=\pm \infty }$ se verifica. Tal função ${\displaystyle f(x)}$ pode ter múltiplas assíntotas verticais na forma ${\displaystyle x=a}$ para todos os valores de ${\displaystyle a}$ que validem ${\displaystyle Q(x)=0}$ e não sejam descontinuidades removíveis (descontinuidade em um ponto apenas)^[4].

Assíntota horizontal

O gráfico da função racional ${\displaystyle f(x)={\frac {P(x)}{Q(x)}}}$ terá uma assíntota horizontal em ${\displaystyle y=b}$ se algum dos limites ${\displaystyle \lim _{x\to \pm \infty }f(x)=b}$ se verifica^[4].

Seja ${\displaystyle m}$ o grau do polinômio ${\displaystyle P(x)}$ e ${\displaystyle n}$ o grau do polinômio ${\displaystyle Q(x)}$, podemos ter três situações:

• ${\displaystyle f(x)}$ terá uma assíntota horizontal em ${\displaystyle y=b}$ se ${\displaystyle m=n}$.
• ${\displaystyle f(x)}$ terá uma assíntota horizontal em ${\displaystyle y=0}$ se ${\displaystyle m<n}$.
• ${\displaystyle f(x)}$ não terá uma assíntota horizontal se ${\displaystyle m>n}$.

Referências

1. «Definition of RATIONAL FUNCTION». www.merriam-webster.com (em inglês). Consultado em 25 de setembro de 2020
2. Bizelli 2019.
3. Almeida, Luís Borges (Março de 2012). «Decomposição em Frações Simples» (PDF). ISR - Instituto de Sistemas e Robótica | Lisboa. Consultado em 25 de setembro de 2020
4. «Funções Racionais». www.educ.fc.ul.pt. Instituto de Educação - Universidade de Lisboa. 2000. Consultado em 25 de setembro de 2020