Top Qs
Linha do tempo
Chat
Contexto
Sete pontes de Königsberg
problema clássico na teoria dos grafos Da Wikipédia, a enciclopédia livre
Remove ads
Sete pontes de Königsberg, ou, na sua forma portuguesa, de Conisberga, é um famoso problema histórico da matemática resolvido por Leonhard Euler em 1736, cuja solução negativa originou a teoria dos grafos.[1]
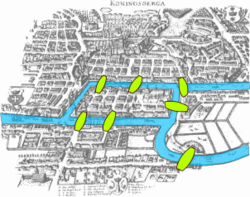


O problema é baseado na cidade de Königsberg (território da Prússia até 1945, atual Kaliningrado), que é cortada pelo Rio Prególia, onde há duas grandes ilhas que, juntas, formam um complexo que na época continha sete pontes, conforme mostra a figura ao lado. Das sete pontes originais, uma foi demolida e reconstruída em 1935, duas foram destruídas durante a Segunda Guerra Mundial - especificamente durante o bombardeamento de Königsberg, em agosto de 1944.[2] e outras duas foram demolidas para dar lugar a uma única via expressa. Atualmente apenas duas pontes são da época de Leonhard Euler.
Discutia-se nas ruas da cidade a possibilidade de atravessar todas as pontes sem repetir nenhuma. Havia-se tornado uma lenda popular a possibilidade da façanha quando Euler, em 1736, provou que não existia caminho que possibilitasse tais restrições.
Euler usou um raciocínio muito simples. Transformou os caminhos em linhas e suas intersecções em pontos, criando possivelmente o primeiro grafo da história. Então percebeu que só seria possível atravessar o caminho inteiro passando uma única vez em cada ponte se houvesse exatamente zero ou dois pontos de onde saísse um número ímpar de caminhos. A razão de tal coisa é que de cada ponto deve haver um número par de caminhos, pois será preciso um caminho para "entrar" e outro para "sair". Os dois pontos com caminhos ímpares referem-se ao início e ao final do percurso, pois estes não precisam de um para entrar e um para sair, respectivamente. Se não houver pontos com número ímpar de caminhos, pode-se (e deve-se) iniciar e terminar o trajeto no mesmo ponto, podendo esse ser qualquer ponto do grafo. Isso não é possível quando temos dois pontos com números ímpares de caminhos, sendo obrigatoriamente um o início e outro o fim.
Remove ads
As sete pontes
Ver também
Referências
- Peter Taylor (2000). Australian Mathematics Trust, ed. «What Ever Happened to Those Bridges?». Consultado em 12 de abril de 2010. Arquivado do original em 19 de março de 2012
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads







