5-celule

În geometrie 5-celule^[a] este un obiect din spațiul cvadridimensional mărginit de 5 celule tetraedrice. Este, de asemenea, cunoscut sub numele de C₅.^[1] Este 4-simplexul, politopul ${\displaystyle \alpha _{4}}$ al lui Coxeter,^[2] cel mai simplu posibil 4-politop regulat convex, fiind analogul 4-dimensional al tetraedrului din trei dimensiuni și al triunghiului din două dimensiuni. Un 5-celule este o piramidă 4-dimensională cu o bază tetraedrică.

5-celule regulat (4-simplex, pentatop)
Diagramă Schlegel (vârfuri și laturi)
Tip	4-politop regulat convex
Simbol Schläfli	{3,3,3}
Diagramă Coxeter
Celule	5 {3,3}
Fețe	10 {3}
Laturi	10
Vârfuri	5
Figura vârfului	(tetraedru)
Poligon Petrie	pentagon
Grup Coxeter	A4, [3,3,3]
Dual	autodual
Proprietăți	convex, izogonal, izotoxal, izoedric
Index uniform	1

Figura vârfului: tetraedru

Desfășurată

Un 5-celule regulat este mărginit de 5 tetraedre regulate și este unul dintre cele șase 4-politopuri regulate convexe, având simbolul Schläfli {3,3,3}.

5-celule este o soluție la problema: Faceți 10 triunghiuri echilaterale, toate de aceeași dimensiune, folosind 10 bețișoare identice, unde fiecare latură a fiecărui triunghi este exact un singur bețișor”. Nu există nicio soluție în trei dimensiuni.

Anvelopa convexă a unui 5-celule și a dualului său (presupunând că sunt congruente) este 30-celule bisfenoidal, dual al 5-celule bitrunchiat.

Geometrie

5-celule este un politop autodual, iar figura vârfului său este un tetraedru. Intersecția sa maximă cu spațiul tridimensional este prisma triunghiulară. Unghiul diedru al acestuia este cos⁻¹(1/4), sau aproximativ 75,52°.

Configurație

Matricea sa de configurație este prezentată mai jos. Rândurile și coloanele corespund vârfurilor, laturilor, fețelor și [[celulă (geometrie) |celulelor. Numerele diagonale spun câte din fiecare element apar în întregul 5-celule. Celelalte numere spun câte elemente ale coloanei apar în sau la elementul rândului. Deoarece este un politop autodual, matricea sa este identică după rotirea sa cu 180 de grade.^[3]

${\displaystyle {\begin{bmatrix}{\begin{matrix}5&4&6&4\\2&10&3&3\\3&3&10&2\\4&6&4&5\end{matrix}}\end{bmatrix}}}$

Construcție

5-celule poate fi construit dintr-un tetraedru adăugând un al 5-lea vârf astfel încât să fie echidistant de toate celelalte vârfuri ale tetraedrului. (5-celule este o piramidă 4-dimensională cu o bază tetraedrică și patru fețe tetraedrice.)

Cel mai simplu set ce coordonate este: (2,0,0,0), (0,2,0,0), (0,0,2,0), (0,0,0,2), (φ,φ,φ,φ), cu lungimea laturii de 2√2, unde φ este secțiunea de aur.^[4]

Coordonatele carteziene ale vârfurilor unui 5-celule regulat centrate în origine având lungimea laturii 2 și raza √1,6 sunt:

${\displaystyle \left({\frac {1}{\sqrt {10}}},\ {\frac {1}{\sqrt {6}}},\ {\frac {1}{\sqrt {3}}},\ \pm 1\right)}$

${\displaystyle \left({\frac {1}{\sqrt {10}}},\ {\frac {1}{\sqrt {6}}},\ {\frac {-2}{\sqrt {3}}},\ 0\right)}$

${\displaystyle \left({\frac {1}{\sqrt {10}}},\ -{\sqrt {\frac {3}{2}}},\ 0,\ 0\right)}$

${\displaystyle \left(-2{\sqrt {\frac {2}{5}}},\ 0,\ 0,\ 0\right)}$

Alt set de coordonate centrate în origine în 4-spațiu poate fi văzut ca o hiperpiramidă cu o bază tetraedrică regulată în 3-spațiu, cu lungimea laturii 2√2 și raza √3,2:

${\displaystyle \left(1,1,1,{\frac {-1}{\sqrt {5}}}\right)}$

${\displaystyle \left(1,-1,-1,{\frac {-1}{\sqrt {5}}}\right)}$

${\displaystyle \left(-1,1,-1,{\frac {-1}{\sqrt {5}}}\right)}$

${\displaystyle \left(-1,-1,1,{\frac {-1}{\sqrt {5}}}\right)}$

${\displaystyle \left(0,0,0,{\frac {4}{\sqrt {5}}}\right)}$

Vârfurile unui 4-simplex (cu latura √2 și raza 1) pot fi construite mai simplu pe un hiperplan în 5-spațiu, ca permutări (distincte) de (0,0,0,0,1) sau (0,1,1,1,1); în aceste poziții este o fațetă, a unui 5-ortoplex (sau a 5-simplexului rectificat).

Elicea Boerdijk–Coxeter

Desfășurata 2D și poligonul Petrie al 5-celule

Un 5-celule poate fi construit ca elicea Boerdijk–Coxeter a cinci tetraedre înlănțuite, pliate într-un inel 4-dimensional. Cele 10 fețe triunghiulare pot fi văzute într-o desfășurată 2D într-o pavare triunghiulară, cu 6 triunghiuri în jurul fiecărui vârf, deși plierea în 4-spațiu face ca laturile să coincidă. Laturile violete sunt poligonul Petrie al 5-celulei.

Proiecții

Un 5-celule se proiectează în planul Coxeter A₄ ca un pentagon regulat și pentagramă.
Format:4-simplex Coxeter plane graphs

Proiecții în tridimensional
Proiecție stereografică tip cadru de sârmă (laturi proiectate pe o 3-sferă)	Proiecție 3D a unui 5-celule executând o rotație simplă
Proiecția unui 5-celule cu un vârf în față are o anvelopă vizibilă tetraedrică. Vârful cel mai apropiat al 5-celule este cel din centrul tetraedrului, cu roșu. Cea mai îndepărtată celulă se proiectează pe anvelopa tetraedrică propriu-zisă, în timp ce celelalte 4 celule se proiectează pe cele 4 regiuni tetraedrice, aplatizate (degenerate în proiecția 3D), care înconjoară vârful central.	Proiecția unui 5-celule cu o latură în față este o bipiramidă triunghiulară a anvelopei. Cea mai apropiată latură (cu roșu) se proiectează pe axa bipiramidei, cele trei celule care o înconjoară unt proiectate în 3D ca 3 volume tetraedrice dispuse în jurul acestei axe la 120 de grade unul față de celălalt. Restul de 2 celule se proiectează pe cele două jumătăți ale bipiramidei și se află pe fața îndepărtată a politopului.
Proiecția unui 5-celule cu o față în față are, de asemenea, o anvelopă vizibilă de bipiramidă triunghiulară. Cea mai apropiată față este colorată în roșu. Cele două celule care se întâlnesc pe această față se proiectează către cele două jumătăți ale bipiramidei. Celelalte trei celule se află pe partea îndepărtată a politopului 4D și pentru claritate sunt eliminate din imagine. Acestea sunt dispuse în jurul axei centrale a bipiramidei, la fel ca în proiecția cu i latură în față.	Proiecția unui 5-celule cu o celulă în față are o anvelopă tetraedrică. Cea mai apropiată celulă se proiectează pe întreaga anvelopă și în 4D ascunde celelalte 4 celule; prin urmare, nu sunt redate aici.

5-celule neregulat

Există multe forme de simetrie inferioară, inclusiv cele ale figurii vârfului politopului uniform:

Simetrie	[3,3,3] Ordinul 120	[3,3,1] Ordinul 24	[3,2,1] Ordinul 12	[3,1,1] Ordinul 6	[5,2]+ Ordinul 10
Nume	5-celule regulat	Piramidă tetraedrică	Piramidă triunghiular-piramidală		Hiperbisfenoid pentagonal
Schläfli	{3,3,3}	{3,3} ∨ ( )	{3} ∨ { }
Exemple, Figura vârfului	5-simplex	5-simplex trunchiat	5-simplex bitrunchiat	5-simplex cantitrunchiat	Fagure 4-simplex omnitrunchiat

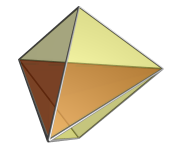
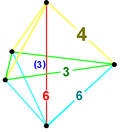
Piramida tetraedrică este un caz particular al unui 5-celule, o piramidă poliedrică având drept bază un tetraedru regulat într-un hiperplan din 3-spațiu și drept apex punctul de deasupra hiperplanului. Cele patru laturi ale piramidei sunt formate din celule tetraedrice.

Multe 5-politopuri uniforme figuri ale vârfului piramida tetraedrică:

Simetrie [3,3,1], ordinul 24

Diagramă Schlegel
Nume Coxeter	{ }×{3,3,3}	{ }×{4,3,3}	{ }×{5,3,3}	t{3,3,3,3}	t{4,3,3,3}	t{3,4,3,3}

Alte 5-politopuri uniforme au figuri ale vârfurilor 5-celule neregulate. Simetria unei figuri a vârfului unui politop uniform este notată prin eliminarea nodurilor inelate ale diagramei Coxeter.

Simetrie	[3,2,1], ordinul 12		[3,1,1], ordinul 6		[2+,4,1], ordinul 8	[2,1,1], ordinul 4
Diagramă Schlegel
Nume Coxeter	t12α5	t12γ5	t012α5	t012γ5	t123α5	t123γ5

Simetrie	[2,1,1], ordinul 2			[2+,1,1], ordinul 2	[ ]+, ordinul 1
Diagramă Schlegel
Nume Coxeter	t0123α5	t0123γ5	t0123β5	t01234α5	t01234γ5

Compuși

Compus de două 5-celule

Compusul de două 5-celule în configurație duală poate fi văzut ca proiecție în planul Coxeter A5, cu vârfurile și laturile celor două 5-celule colorate roșu, respectiv albastru. Acest compus are simetria de ordinul 240 [[3,3,3]]. Intersecția acestor două 5-celule este un 5-celule bitrunchiat uniform. = ∩ .

Acest compus poate fi văzut ca analogul 4D al hexagramei 2D {⁶⁄₂} și al compusului de două tetraedre 3D.

Politopuri și faguri asociați

5 celule este cel mai simplu dintre cele 9 4-politopuri uniforme construite din grupul Coxeter [3,3,3].

Schläfli	{3,3,3}	t{3,3,3}	r{3,3,3}	rr{3,3,3}	2t{3,3,3}	tr{3,3,3}	t0,3{3,3,3}	t0,1,3{3,3,3}	t0,1,2,3{3,3,3}
Diagramă Coxeter
Diagramă Schlegel

Figuri 1k2 în n dimensiuni
Spațiu	Finit						Euclidian	Hiperbolic
n	3	4	5	6	7	8	9	10
Grup Coxeter	E3=A2A1	E4=A4	E5=D5	E6	E7	E8	E9 = ${\displaystyle {\tilde {E}}_{8}}$ = E8+	E10 = ${\displaystyle {\bar {T}}_{8}}$ = E8++
Diagramă Coxeter
Simetrie (ordin)	[3−1,2,1]	[30,2,1]	[31,2,1]	[[32,2,1]]	[33,2,1]	[34,2,1]	[35,2,1]	[36,2,1]
Grup (ordin)	12	120	1 920	103 680	2 903 040	696 729 600	∞
Graf							-	-
Nume	1−1,2	102	112	122	132	142	152	162

Figuri 2k1 în n dimensiuni
Spațiu	Finit						Euclidian	Hiperbolic
n	3	4	5	6	7	8	9	10
Grup Coxeter	E3=A2A1	E4=A4	E5=D5	E6	E7	E8	E9 = ${\displaystyle {\tilde {E}}_{8}}$ = E8+	E10 = ${\displaystyle {\bar {T}}_{8}}$ = E8++
Diagramă Coxeter
Simetrie (ordin)	[3−1,2,1]	[30,2,1]	[[31,2,1]]	[32,2,1]	[33,2,1]	[34,2,1]	[35,2,1]	[36,2,1]
Grup (ordin)	12	120	384	51 840	2 903 040	696 729 600	∞
Graf							-	-
Nume	2−1,1	201	211	221	231	241	251	261

Din secvența 4-politopurilor regulate fac parte: tesseractul {4,3,3} și 120-celule {5,3,3} din 4-spațiul euclidian și fagurele pavare hexagonală {6,3,3} din spațiul hiperbolic. Toate acestea au ca figură a vârfului tetraedrul.

Politopuri {p,3,3}
Spațiu		S3			H3
Formă		Finit			Paracompact	Necompact
Nume		{3,3,3}	{4,3,3}	{5,3,3}	{6,3,3}	{7,3,3}	{8,3,3}	...{∞,3,3}
Imagine
Celule {p,3}		{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

5-celule este unul dintre cele 4-politopuri regulate cu celule tetraedrice, împreună cu 16-celule {3,3,5} și 600-celule {3,3,5} din spațiul euclidian. Fagurele tetraedric de ordinul 6 {3,3,6} din spațiul hiperbolic are și el celule tetraedrice.

Politopuri {3,3,p}
Spațiu	S3			H3
Formă	Finit			Paracompact	Necompact
Nume	{3,3,3}	{3,3,4}	{3,3,5}	{3,3,6}	{3,3,7}	{3,3,8}	... {3,3,∞}
Imagine
Figura vârfului	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}

Politopuri {3,p,3}
Spațiu	S3		H3
Formă	Finit		Compact	Paracompact	Necompact
{3,p,3}	{3,3,3}	{3,4,3}	{3,5,3}	{3,6,3}	{3,7,3}	{3,8,3}	... {3,∞,3}
Imagine
Celule	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	[[{3,∞}
Figura vârfului	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

Faguri regulați {p,3,p}
Spațiu	S3	E3	H3
Formă	Finit	Afin	Compact	Paracompact	Necompact
Nume	{3,3,3}	{4,3,4}	{5,3,5}	{6,3,6}	{7,3,7}	{8,3,8}	...{∞,3,∞}
Imagine
Celule	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}
Figura vârfului	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}

Note explicative

1. „5-celule” este o prescurtare a expresiei din limba română „un politop cvadridimensional format din 5 celule”, plural „două sau mai multe politopuri cvadridimesnsionale formate din câte 5 celule”, expresii care se acordă corespunzător, deci se vorbește despre „un/acel 5-celule”, nu „o/acea 5-celule”, respectiv „unele/acele 5-celule”', nu „unii/acei 5-celule”. La fel la celelalte politopuri ale căror nume este de forma „n-celule”.