Доминирующее множество

В теории графов доминирующее множество для графа G = (V, E) — это подмножество D множества вершин V, такое, что любая вершина не из D смежна хотя бы одному элементу из D. Число доминирования γ(G) — это число вершин в наименьшем доминирующем множестве G.

Доминирующее множество (красные вершины).

Задача о доминирующем множестве заключается в проверке, верно ли неравенство γ(G) ≤ K для заданного графа G и числа K. Задача является классической NP-полной проблемой разрешимости в теории вычислительной сложности^[1]. Таким образом полагают, что не существует эффективного алгоритма для нахождения наименьшего доминирующего множества для заданного графа.

Рисунки (a)-(c) справа показывают три примера доминирующих множеств графа. В этих примерах каждая белая вершина смежна по меньшей мере одной красной вершине и говорят, что белые вершины доминируются красными вершинами. Доминирующее число этого графа равно 2 — примеры (b) и (c) показывают, что существует доминирующее множество с 2 вершинами, и можно проверить, что для данного графа не существует доминирующего множества лишь с одной вершиной.

История

Как заметили Хедееними и Ласкар^[2], задача доминирования изучалась с 1950-х годов, но число исследований по доминированию существенно возросло в середине 1970-х. Их библиография включает более 300 статей, связанных с доминированием на графах.

Границы

Пусть G — граф с n ≥ 1 вершинами, и пусть Δ — максимальная степень графа. Известны следующие границы γ(G)^[3]:

• Одна вершина может доминировать максимум Δ других вершин, поэтому γ(G) ≥ n/(1 + Δ).
• Множество всех вершин является доминирующим множеством в любом множестве, поэтому γ(G) ≤ n.
• Если в графе G нет изолированных вершин, то имеется два раздельных доминирующих множества в G. См. доматическое разложение для деталей. Таким образом, для графов без изолированных вершин выполняется γ(G) ≤ n/2.

Независимая доминация

Доминирующие множества тесно связаны с независимыми множествами — независимое множество является доминирующим тогда и только тогда, когда оно является наибольшим независимым множеством, так что любое наибольшее независимое множество^[4] в графе является также наименьшим доминирующим множеством. Число независимого доминирования i(G) графа G — это размер наименьшего независимого доминирующего множества (или, эквивалентно, минимальный размер наибольших независимых множеств).

Минимальное доминирующее множество в графе не обязательно будет независимым, но размер минимального доминирующего множества всегда меньше либо равен размеру минимального наибольшего независимого множества, то есть γ(G) ≤ i(G).

Существуют семейства графов, в которых минимальное наибольшее независимое множество является минимальным доминирующим множеством. Например, Аллан и Ласкар^[5] показали, что γ(G) = i(G), если G не имеет клешней.

Граф G называется доминантно-совершенным графом, если γ(H) = i(H) в любом порождённом подграфе H графа G. Поскольку порождённый подграф свободного от клешней графа является свободным от клешней, отсюда следует, что любой свободный от клешней граф является доминантно-совершенным^[6].

Примеры

Фигуры (a) и (b) демонстрируют независимые доминантные множества, в то время как фигура (c) демонстрирует множество, не являющееся независимым.

Для любого графа G его рёберный граф L(G) является свободным от клешней, а потому минимальное наибольшее независимое множество в L(G) является также минимальным доминирующим множеством в L(G). Независимое множество в L(G) соответствует паросочетанию в G, а доминирующее множество в L(G) соответствует рёберному доминирующему множеству^[англ.] в G. Таким образом, минимальное наибольшее паросочетание имеет тот же размер, что и минимальное рёберное доминирующее множество.

Алгоритмы и вычислительная сложность

Существует пара L-приведений полиномиального времени между задачей минимального доминирующего множества и задачей о покрытии множества^[7]. Эти редукции (см. ниже) показывают, что эффективный алгоритм для задачи о минимальном доминирующем множестве дал бы эффективный алгоритм для задачи о покрытии множества, и наоборот. Более того, приведения сохраняют аппроксимационный коэффициент — для любого α, α-аппроксимирующий алгоритм полиномиального времени нахождения минимального доминирующих множеств обеспечил бы α-аппроксимирующий алгоритм полиномиального времени для задачи о покрытии множества, и наоборот. Обе задачи, фактически, являются Log-APX-полными^[8].

Задача о покрытии множества является хорошо известной NP-трудной задачей — задача о покрытии множества в варианте проблемы разрешимости была одной из 21 NP-полных задач Карпа, для которой была доказана NP-полнота уже в 1972. Возможность приведения показывает, что задача о доминирующем множестве является также NP-трудной.

Аппроксимируемость задачи о покрытии множества также хорошо понятна — логарифмический множитель аппроксимации может быть найден с использованием простого жадного алгоритма, а нахождение сублогарифмического и логарифмического множителя является NP-трудной задачей. Конкретнее — жадный алгоритм даёт аппроксимирующий множитель 1 + log |V| для минимального доминирующего множества, а Раз и Сафра ^[9] показали, что никакой алгоритм не даст аппроксимирующий множитель лучше C*log |V| для некоторого C > 0, если только не P = NP.

L-приведения

Следующая пара приведений^[7] показывает, что задача о минимальном доминирующего множества и задача о покрытии множества эквивалентны по L-приведению — если дана одна задача, мы можем построить эквивалентную постановку другой задачи.

От доминирующего множества к покрытию множества. Если задан граф G = (V, E) с V = {1, 2, …, n}, строим покрытие множества (U, S) следующим образом: Множество U равно V, а семейство подмножеств равно S = {S₁, S₂, …, S_n}, где S_vсостоит из вершины v и всех вершин, смежных v вершин из G.

Теперь, если D является доминирующим множеством в G, то C = {S_v : v ∈ D} является допустимым решением для задачи покрытия с |C| = |D|. Обратно, если C = {S_v : v ∈ D} является допустимым решением для задачи покрытия, то D является доминирующим множеством для G с |D| = |C|.

Отсюда — размер минимального доминирующего множества для G равен размеру минимального покрытия множества для (U, S). Более того, существует простой алгоритм, который отображает доминирующее множество в покрытие множества того же размера, и наоборот. В частности, эффективный α-аппроксимационный алгоритм для покрытия множества даёт эффективный α-аппроксимационный алгоритм для минимальных доминирующих множеств.

Например, если задан граф G, показанный справа, мы строим покрытие множества с множеством U = {1, 2, …, 6} и подмножествами S₁ = {1, 2, 5}, S₂ = {1, 2, 3, 5}, S₃ = {2, 3, 4, 6}, S₄ = {3, 4}, S₅ = {1, 2, 5, 6} и S₆ = {3, 5, 6}. В этом примере D = {3, 5} является доминирующим множеством для G — оно соответствует покрытию C = {S₃, S₅}. Например, вершина 4 ∈ V доминируется вершиной 3 ∈ D, а элемент 4 ∈ U содержится во множестве S₃ ∈ C.

Из покрытия множества к доминирующему множеству. Пусть (S, U) — решение задачи покрытия множества с совокупностью U и семейством подмножеств S = {S_i : i ∈ I}. Мы предполагаем, что U и множество индексов I не пересекаются. Строим граф G = (V, E) следующим образом. В качестве множества вершин возьмём V = I ∪ U. Определяем ребро {i, j} ∈ E между каждой парой i, j ∈ I, а также ребро {i, u} для каждого i ∈ I и u ∈ S_i. То есть G является расщепляемым графом — I является кликой и U является независимым множеством.

Теперь, если C = {S_i : i ∈ D} является допустимым решением задачи покрытия множества для некоторого подмножества D ⊆ I, тогда D является доминирующим множеством для G с |D| = |C|: Первое, для любой вершины u ∈ U существует i ∈ D, такой, что u ∈ S_i, и, по построению, u и i смежны в G. Отсюда — u доминируется вершиной i. Второе, поскольку D должен быть непустым, любая i ∈ I смежна вершине в D.

Обратно — пусть D является доминирующим множеством для G. Тогда можно построить другое доминирующее множество X, такое, что |X| ≤ |D| и X ⊆ I — просто заменяет каждую вершину u ∈ D ∩ U соседней к u вершиной i ∈ I. Тогда C = {S_i : i ∈ X} является допустимым решением задачи покрытия с |C| = |X| ≤ |D|.

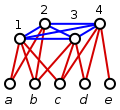
Рисунок справа показывает построение для U = {a, b, c, d, e}, I = {1, 2, 3, 4}, S₁ = {a, b, c}, S₂ = {a, b}, S₃ = {b, c, d}, and S₄ = {c, d, e}.

В этом примере C = {S₁, S₄} является покрытием множества. Оно соответствует доминирующему множеству D = {1, 4}.

D = {a, 3, 4} — другое доминирующее множество для графа G. Ели D задано, мы можем построить доминирующее множество X = {1, 3, 4}, которое не превосходит D и которое является подмножеством I. Доминирующее множество X соответствует покрытию множества C = {S₁, S₃, S₄}.

Специальные случаи

Если граф имеет максимальную степень Δ, то жадный аппроксимационный алгоритм находит O(log Δ)-аппроксимацию минимального доминирующего множества. Также пусть d_g является мощностью доминирующего множества, полученного с помощью жадного аппроксимационного алгоритма, тогда выполняется следующее отношение: d_g ≤ N+1 — ${\displaystyle {\sqrt {2M+1}}}$, где N — число узлов, а M — число рёбер в заданном неориентированном графе ^[10]. Для фиксированного Δ это означает принадлежность задачи поиска доминирующего множества классу APX. Фактически задача является APX-полной^[11].

Алгоритм допускает PTAS для специальных случаев, таких как графы единичных кругов и планарные графы^[12]. Минимальное доминирующее множество может быть найдено за линейное время в параллельно-последовательных графах^[13].

Точные алгоритмы

Минимальное доминирующее множество графа с n вершинами может быть найдено за время O(2ⁿn) путём просмотра всех подмножеств вершин. Фомин, Грандони и Кратч показали^[14], как найти минимальное доминирующее множество за время O(1.5137ⁿ), при использовании экспоненциальной памяти, и за время O(1.5264ⁿ), при использовании полиномиальной памяти. Более быстрый алгоритм, работающий за время O(1.5048ⁿ), был найден фон Роем, Недерлофом и фон Дейком ^[15], которые показали, что число минимальных доминирующих множеств может быть вычислено за указанное время. Число минимальных доминирующих множеств не превосходит 1.7159ⁿ и все такие множества могут быть перечислены за время O(1.7159ⁿ)^[16] .

Параметрическая сложность

Поиск доминирующего множества размера k играет центральную роль в теории параметрической сложности. Задача является наиболее известной W[2]-полной^[англ.] задачей и используется во многих случаях для показа трудноразрешимости задачи путём приведения её к задаче поиска доминирующего множества. В частности, задача не является фиксированно-параметрически разрешимой^[англ.] (ФПР) в том смысле, что не существует алгоритма со временем работы f(k)n^O(1) для любой функции f, разве только W-иерархия не сворачивается в FPT=W[2].

С другой стороны, если входной граф планарен, задача остаётся NP-трудной, но алгоритм с фиксированным параметром известен. Фактически задача имеет ядро с размером, линейным по k^[17], а время работы, экспоненциальное по √k и кубическое по n, может быть достигнуто при применении динамического программирования к разбиению на ветви ядра^[18]. Более обще, задача доминирующего множества и многие варианты задачи являются фиксированно-параметрически разрешимыми, если параметризация проводится как по размеру доминирующего множества, так и по размеру наименьшего запрещённого полного двудольного подграфа. То есть задача является ФПР на графах без биклик, достаточно общего класса разреженных графов, в который входят планарные графы^[19].

Варианты

Гипотеза Визинга связывает число доминирования прямого произведения графов с числами доминирования его множителей.

Имеется множество статей о связном доминирующем множестве. Если S является связным доминирующим множеством, можно образовать остовное дерево графа G, в котором S образует множество нелистовых вершин дерева. Обратно, если T является остовным деревом графа с более чем двумя вершинами, нелистовые вершины T образуют связное доминирующее множество. Таким образом, поиск минимальных связных доминирующих множеств эквивалентен поиску остовных деревьев с максимальным возможным числом листьев.

Полное доминирующее множество — это множество вершин, таких, что все вершины графа (включая вершины самого доминирующего множества) имеют соседей в доминирующем множестве. Рисунок (c) выше показывает доминирующее множество, являющееся связным доминирующим множеством и полным доминирующим множеством одновременно. На рисунках (a) и (b) доминирующие множества не являются ни теми, ни другими.

k-кортежное доминирующее множество — это множество вершин, таких, что каждая вершина в графе имеет по меньшей мере k соседей в множестве. (1+log n)-аппроксимация минимального k-кортежного доминирующего множества может быть найден за полиномиальное время ^[20]. Подобно этому, k-доминирующее множество — это множество вершин, такое, что каждая вершина, не принадлежащая множеству, имеет по меньшей мере k соседей в множестве. В то время как любой граф допускает k-доминирующее множество, только графы с минимальной степенью k-1 допускают k-кортежное доминирующее множество. Однако, даже если граф допускает k-кортежное доминирующее множество, минимальное k-кортежное доминирующее множество может быть почти в k раз больше минимального k-доминирующего множества для того же графа ^[21]. (1.7+log Δ)-аппроксимация минимального k-доминирующего множества может быть найдена также в полиномиальное время.

Доматическое разложение — это разложение вершин на непересекающиеся доминирующие множества. Доматическое число — это максимальный размер доматического разложения.

Вечное доминирующее множество — это динамическая версия доминирования, в которой вершина v в доминирующем множестве D выбирается и заменяется соседней u (u не из D) таким образом, что модифицированное множество D также является доминирующим и этот процесс может быть повторён для любой конечной последовательности выборов вершин v.

См. также

• Задача о покрытии множества
• Число зависимости^[англ.]