Квазистатический процесс

Эта статья — о понятии термодинамики. Об аналогичном понятии в других науках см. Квазистационарный процесс.

Квазистатический процесс в термодинамике — относительно медленный (в пределе — бесконечно медленный) процесс (то есть переход термодинамической системы из одного состояния в другое^[1]), длительность протекания которого намного превышает характерные времена релаксации системы^{[2][K 1]}. При этом система проходит через последовательность бесконечно близких квазиравновесных состояний^[4][5], и квазистатический процесс может также называться квазиравновесным. Совокупность бесконечно малых квазистатических процессов есть конечный квазистатический процесс^{[6][K 2]}.

Образующие цикл Карно квазистатические изотермы (1—2 и 3—4) и адиабаты (2—3 и 4—1) на диаграмме Эндрюса в координатах давление — объём

Значение квазистатических процессов

Т. А. Афанасьева-Эренфест показала (1925), что понятие об обратимости и необратимости процессов имеет лишь косвенное отношение к термодинамике, то есть классическая термодинамика должна, по её мнению, строиться как теория равновесных состояний и квазистатических процессов^[6]. Квазистатические процессы по сию пору иногда называют обратимыми лишь в силу восходящей ко временам Клаузиуса традиции^{[K 3]}, хотя не всякий квазистатический процесс является обратимым или равновесным^{[K 4]}. Однако в классической термодинамике состояний и идеальных процессов (термостатике)^{[K 5]}, термины обратимые процессы и квазистатические процессы часто рассматривают как синонимы^{[12][13][14][15][16][17][18][19][20][21][22][23]}.

Медленность квазистатических процессов служит основанием для того, чтобы не учитывать полагаемые равными нулю скорости протекания таких процессов, то есть использование представления о квазистатичности процессов есть способ исключить время из числа переменных, учитываемых классической термодинамикой состояний и идеальных процессов (термостатикой) и рассматривать процесс, то есть изменение состояния системы во времени^[24] без использования этой физической величины в качестве термодинамической переменной^{[25][26][27][28][29][30][31][32][33][34][35]}. Время, однако, может входить в термостатические соотношения в качестве параметра^[36], например, в формулы вычисления мощности.

Опыт показывает, что число переменных, полностью описывающих равновесное состояние, меньше, чем требуется для описания любого неравновесного состояния^[37][38]. Поэтому допущение о квазистатичности реального процесса и связанное с этим сокращение числа принимаемых во внимание переменных существенно упрощает термодинамический анализ рассматриваемого процесса^{[39][40][41][42][43]}. При этом оказывается, что аппроксимация идущего с конечной скоростью реального нестатического процесса его идеализированной бесконечно медленной квазистатической моделью позволяет проводить вычисления с достаточной точностью для большого класса практических задач^[44][32]. С другой стороны, выводы, получаемые термодинамикой для квазистатических процессов, носят характер своего рода теорем о предельных значениях термодинамических величин — полезной работы, КПД тепловой машины и т. п.^[45]

Условия квазистатичности процесса

Пусть X — некоторая характеризующая процесс термодинамическая величина. В термостатике для получения количественных зависимостей типа X = … рассматривают только квазистатические процессы^[21], тогда как для нестатических процессов термостатика даёт качественные результаты вида X < … или X > … Иными словами, термодинамический процесс является квазистатическим, если характеризующие его величины могут быть найдены методами термостатики^[46].

Квазистатические процессы не реализуются в природе, но являются хорошей моделью для процессов, протекающих достаточно медленно по сравнению с процессами установления термодинамического равновесия в системе. Условие «медленности» относительно, а именно, сравнивают время ${\displaystyle t}$ квазистатического изменения значения некоторой термодинамической переменной ${\displaystyle x}$ на величину ${\displaystyle \Delta x}$ и время релаксации ${\displaystyle \tau }$ после мгновенного изменения этого же значения ${\displaystyle x}$ на величину ${\displaystyle \Delta x}$: при квазистатическом изменении переменной ${\displaystyle t\gg \tau }$^[47].

Графическое изображение квазистатических процессов

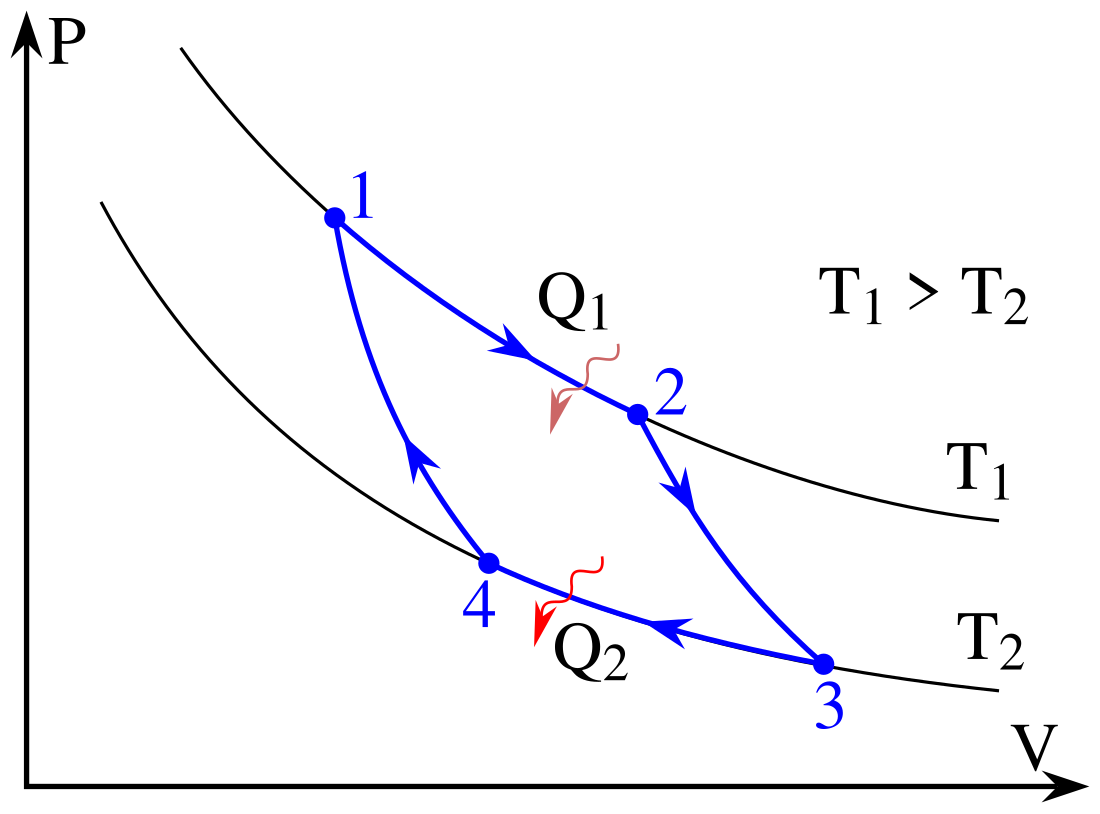
Поскольку для квазистатических процессов время исключено из числа учитываемых переменных, то такой процесс можно геометрически представить в виде непрерывной кривой на термодинамической поверхности^[48][49][50], например на PV-диаграмме Эндрюса^{[51][K 6]}. Изображать графически на термостатических (не содержащих времени термодинамических) диаграммах можно квазиравновесные и только квазиравновесные процессы^[56]; нестатические процессы на термостатических диаграммах отобразить нельзя^{[57][58][55][59]}. Встречающееся в литературе графическое изображение на термостатических диаграммах реальных нестатических процессов, протекающих с конечной скоростью, имеет условный характер^{[60][61][62][63][64]}, когда нестатический процесс аппроксимируют линией (обычно штриховой или пунктирной^{[65][66][67][68][69][70]}), соединяющей два квазиравновесные состояния^[71][67], причём, кроме начальной и конечной, никакая другая точка на этой линии не соответствует промежуточному состоянию термодинамической системы^{[72][73][74][75]}.

Виды квазистатических процессов

В термодинамике наиболее часто рассматриваются следующие виды квазистатических процессов:

• Изохорный процесс — процесс, происходящий при постоянном объёме;
• Изобарный процесс — процесс, происходящий при постоянном давлении;
• Изотермический процесс — процесс, в котором температура остается постоянной;
• Адиабатический процесс Пуассона — процесс, который совершается без подвода или отвода тепла, причем медленно. К примеру, адиабатическое расширение в пустоту не является квазистатическим процессом^{[76][K 7]}. Как и все квазистатические процессы, указанные изменения можно графически изобразить непрерывными линиями, названия которых практически соответствуют названиям самих описываемых процессов — изобарой, изохорой, изотермой и адиабатой.

Терминологические замечания

Термин "квазистатический" (от лат. quasi — как если бы, подобно + static — статический) был предложен К. Каратеодори в 1909 г.^[95] Понятийный аппарат, используемый в том или ином руководстве по классической термодинамике, существенным образом зависит от системы построения/изложения данной дисциплины, используемой автором конкретного пособия. Последователи Р. Клаузиуса строят/излагают термодинамику как теорию обратимых процессов^[96], последователи К. Каратеодори — как теорию квазистатических процессов^[95], а последователи Дж. У. Гиббса — как теорию равновесных состояний и процессов^[97][98]. Ясно, что, несмотря на применение различных описательных дефиниций идеальных термодинамических процессов — обратимых, квазистатических и равновесных, — которыми оперируют упомянутые выше термодинамические аксиоматики, в любой из них все построения классической термодинамики имеют своим итогом один и тот же математический аппарат. Де-факто это означает, что за пределами чисто теоретических рассуждений, то есть в прикладной термодинамике, термины «обратимый процесс», «равновесный процесс» и «квазистатический процесс» рассматривают как синонимы^[99]: всякий равновесный (квазистатический процесс) процесс является обратимым, и наоборот, любой обратимый процесс является равновесным (квазистатическим)^{[100][101][102]}.

См. также

• Необратимый процесс
• Обратимый процесс
• Равновесный процесс

Комментарии

1. Разные термодинамические переменные могут иметь для различных систем и процессов существенно разные времена релаксации. Пусть Z — та переменная, для которой время релаксации τ_max имеет наибольшее значение (его и принимают за время релаксации всей системы) и которая в рассматриваемом процессе изменяется на величину ΔZ. Тогда процесс считают квазистатическим, если в каждый момент времени τ его скорость много меньше средней скорости изменения переменной Z при релаксации, то есть dZ/dτ << ΔZ/τ_max^[3].
2. Может показаться, что к квазистатическому процессу предъявляются взаимоисключающие требования: быть процессом и одновременно быть равновесием, то есть не быть процессом. «Отождествление движения с последовательностью смежных состояний покоя, во время которых движущееся тело находится в равновесии, на первый взгляд кажется абсурдным. Однако движение, составленное из неподвижных состояний, не более и не менее абсурдно, чем длина, составленная из лишенных протяжения точек, или чем время, составленное из не имеющих длительности мгновений» (оригинал^[7], перевод^[8]).
3. Замена постулата Клаузиуса его антитезой, физически абсурдной предпосылкой противоположного содержания, не отражается ни на существе получаемых с его помощью результатов, ни на способе их получения^[9].
4. По вопросу о связи между обратимостью и квазистатичностью (равновесностью) у разных авторов нет единой точки зрения. Вот пример в точности противоположных утверждений двух признанных авторитетов по термодинамике: «квазистатический процесс может быть как обратимым, так и необратимым» (И. Дьярмати) и «любой квазистатический процесс обратим и наоборот» (П. Ландсберг)^[10]. С И. Дьярмати солидарен Л. И. Седов: «…в ряде распространенных учебников авторы ”доказывают”, без специальных оговорок, неверное утверждение, что всякий равновесный процесс обратим»^[11].
5. Термин классическая термодинамика состояний и идеальных процессов использован с тем, чтобы отличить классическую термодинамику (термостатику) от классической термодинамики реальных (нестатических) процессов.
6. Именно квазистатичность позволила Клапейрону ввести (1833)^[52] в термодинамическую практику наглядное графическое изображение процессов^[53][54][55].
7. Реальные процессы дросселирования (процесс Джоуля — Томсона) и расширения газа в пустоту (процесс Джоуля^[77]) необратимы^{[78][79][80][63][81][82]}, но при рассмотрении методами термостатики их мысленно заменяют квазистатическими моделями^[83], допускающими, помимо прочего, изображение этих процессов на термодинамических диаграммах^{[84][85][86][87][88][89][90][91][92][93][94]}.