Лентикулярный растр

Лентикулярный растр^[1] (от лат. lenticula, означающего чечевицу или чечевицеобразное тело) или линзовый растр^[2] — массив из плоско-выпуклых цилиндрических собирающих линз, расположенный над изображением или светочувствительным слоем для считывания или записи растровых цветных или трёхмерных изображений^[3].

Наиболее распространенный пример использования лентикулярных растров — использование в лентикулярной печати для создания изображений с иллюзией движения при смещении головы наблюдателя. В 1970-х годах были популярны открытки, карманные календари и значки с изображением, изменяющимся, если смотреть на него под разными углами. Данный эффект получил название «флип». Этот же принцип положен в основу современных безочковых 3D-телевизоров некоторых производителей^[4].

Ещё одной областью применения линзового растра такой конструкции в 1928 году стало создание цветных киноплёнок Kodacolor с цветоделением при помощи совместной работы лентикулярного растра и цветных светофильтров, встроенных в съёмочный и проекционный объективы^[5]. 16-миллиметровая киноплёнка с таким растром, изготовленным на подложке, выпускалась всего 4 года, и технология была забыта после появления многослойных киноплёнок.

Получение автостереограмм на лентикулярных растрах

Печать многоракурсного изображения

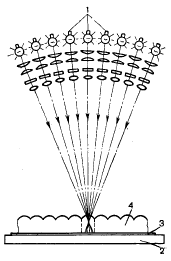
Фотосъёмка с помощью кодирующего растра

Съёмка трёхмерного изображения с помощью кодирующего растра

По дуге вокруг статичного объекта движется камера. Между жёстко прикреплённой к задней стенке камеры фотоплёнкой и объективом находится растр, прижатый к фотоплёнке так, чтобы между ними не было зазора, но растр мог скользить вдоль неё. Одновременно с перемещением камеры между крайними положениями, растр смещается на один период против направления движения камеры^[6]. В результате на плёнке получается закодированное негативное или позитивное кодированное изображение.

Проекционная печать многоракурсных изображений

Проецирование негативных изображений ракурсов через растр на светочувствительный материал. Группа независимых проекторов направлена на одну и ту же доску увеличителя, так что их оптические оси сходятся в одной точке. В каждом проекторе установлен один негатив или слайд из комплекта ракурсов объекта.

Угол обзора лентикулярного растра

Угол зрения линзовидной печати - это диапазон углов, в пределах которых наблюдатель может видеть все изображение. Это определяется максимальным углом, при котором луч может покинуть изображение через правильную лентикулу.

Угол в объективе

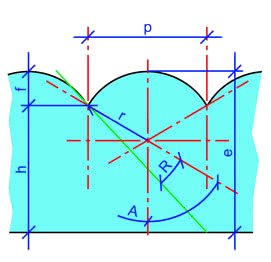
Диаграмма справа показывает зеленый цвет наиболее экстремального луча в линзовидной линзе, который будет правильно преломлен объективом. Этот луч оставляет один край полосы изображения (в правом нижнем углу) и выходит через противоположный край соответствующей лентикулы.

Определения

• ${\displaystyle R}$ - это угол между крайним лучом и нормалью в точке, где он выходит из объектива,
• ${\displaystyle p}$ - высота или ширина каждой линзовидной ячейки,
• ${\displaystyle r}$ - радиус кривизны лентикулы,
• ${\displaystyle e}$ - толщина линзовидной линзы
• ${\displaystyle h}$- толщина подложки ниже криволинейной поверхности линзы и
• ${\displaystyle n}$ - показатель преломления линзы.

Формулы для расчета

${\displaystyle R=A-\arctan \left({p \over h}\right)}$,

где

${\displaystyle A=\arcsin \left({p \over 2r}\right)}$,

${\displaystyle h=e-f}$ iэто расстояние от задней части решетки до края линзы, и

${\displaystyle f=r-{\sqrt {r^{2}-\left({p \over 2}\right)^{2}}}}$.

Угол снаружи объектива

Показатель преломления

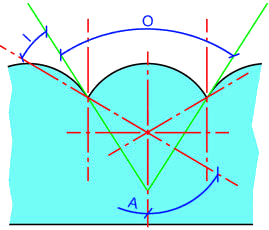
Угол снаружи линзы определяется преломлением луча, определенного выше. Полный угол наблюдения  ${\displaystyle O}$ задается формулой

${\displaystyle O=2(A-I)}$,

где ${\displaystyle I}$ - угол между крайним лучом и нормалью вне объектива. Из закона Снелла,

${\displaystyle I=\arcsin \left({n\sin(R) \over n_{a}}\right)}$,

где ${\displaystyle n_{a}\approx 1.003}$ является коэффициентом преломления воздуха..

Пример

Рассмотрим линзовидную печать с линзами с шагом 336,65 мкм, радиусом кривизны 190,5 мкм, толщиной 457 мкм и показателем преломления 1,557. Полный угол наблюдения ${\displaystyle O}$ составит 64,6 °.

Задняя фокальная плоскость линзовидной сети

Фокусное расстояние объектива рассчитывается по уравнению линзодержателя, которое в этом случае упрощает:

${\displaystyle F={r \over n-1}}$,

где ${\displaystyle F}$- фокусное расстояние объектива.

Задняя фокальная плоскость расположена на расстоянии ${\displaystyle BFD}$ от задней части объектива:

${\displaystyle BFD=F-{e \over n}.}$

Отрицательный BFD указывает, что фокальная плоскость лежит внутри объектива.

В большинстве случаев линзовидные линзы предназначены для того, чтобы задняя фокальная плоскость совпадала с задней плоскостью объектива. Условием для этого совпадения является ${\displaystyle BFD=0}$, или

${\displaystyle e={nr \over n-1}.}$

Это уравнение накладывает связь между толщиной линзы ${\displaystyle e}$  ее радиусом кривизны ${\displaystyle r}$.

Пример

Линзообразная линза в приведенном выше примере имеет фокусное расстояние 342 мкм и фокусное расстояние 48 мкм, что указывает на то, что фокальная плоскость объектива падает на 48 мкм позади изображения, напечатанного на задней стороне объектива.

См. также

• Щелевой растр
• Автостереоскопия
• Растровая фотография
• Растровый экран
• Линза Френеля