Параметрическое семейство

В математике и её приложениях параметрическое семейство — это семейство объектов (множество связанных объектов), чьи различия зависят только от выбранных значений для множества параметров^[1] .

Примеры параметрических семейств: функции, распределения вероятности, кривые, геометрические фигуры.

В теории вероятностей и её приложениях

Основная статья: Статистическое моделирование

Графики функций плотности вероятности для нескольких нормальных распределений (одного параметрического семейства).

Пусть функция плотности вероятности ${\displaystyle f_{X}}$ случайной величины ${\displaystyle X}$ зависит от параметра ${\displaystyle \theta }$. В этом случае функцию можно обозначить как ${\displaystyle f_{X}(\cdot$ ;\theta )} , чтобы обозначить зависимость от параметра ${\displaystyle \theta }$. ${\displaystyle \theta }$ не является аргументом функции и считается зафиксированным. Тем не менее, различные параметры дают различные функции плотности вероятности. Тогда параметрическое семейство плотностей — это множество функций ${\displaystyle \{f_{X}(\cdot$ ;\theta )|\theta \in \Theta \}} , где ${\displaystyle \Theta }$ — пространство параметров, множество всех возможных значений, которые ${\displaystyle \theta }$ может принять. Например, нормальное распределение — это семейство распределений сходных по форме, параметризируемое математическим ожиданием (средним) и дисперсией.^[2][3]

В теории принятия решений двухмоментные модели принятия решений^[англ.] применяются, когда лицо, принимающее решение, сталкивается со случайными величинами из семейства сдвига-масштаба^[англ.] распределения вероятности^{[источник не указан 1536 дней]}.

В алгебре и её приложениях

Трёхмерный график функции Кобба — Дугласа.

В экономике функция Кобба — Дугласа — это семейство производственных функций, параметризированных эластичностью по различным факторам производства^{[источник не указан 1536 дней]}.

График нескольких квадратных многочленов, при изменении одного из трёх коэффициентов независимо от других.

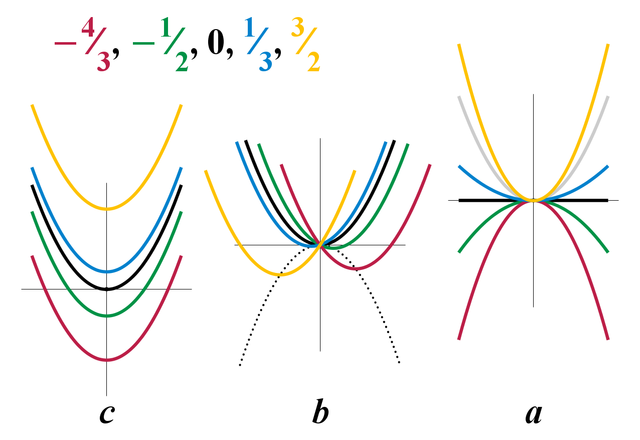
В алгебре квадратные уравнения это семейство уравнений, параметризуемое тремя коэффициентами: при переменной ${\displaystyle x}$ и её квадрате, а также свободным членом^{[источник не указан 1536 дней]}.

См. также

• Семейство (математика)