Поверхность второго порядка

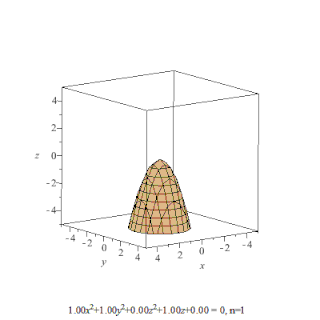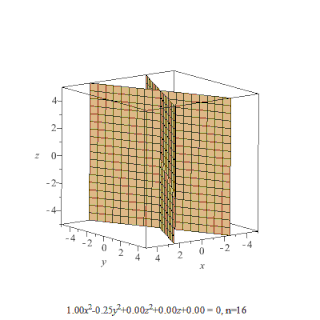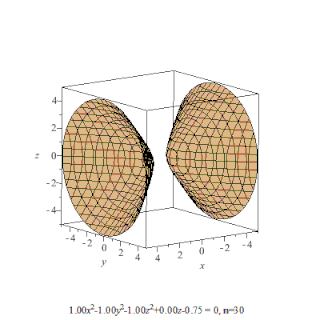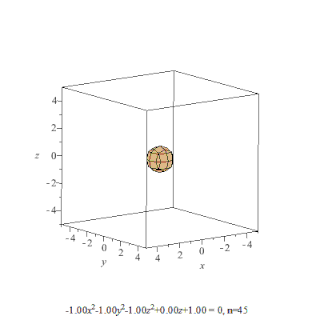
Поверхность второго порядка — геометрическое место точек трёхмерного пространства, прямоугольные координаты которых удовлетворяют уравнению вида

${\displaystyle Ax^{2}+By^{2}+Cz^{2}+Dxy+Eyz+Fxz+Gx+Hy+Iz+J=0}$

в котором по крайней мере один из коэффициентов ${\displaystyle A}$, ${\displaystyle B}$, ${\displaystyle C}$,${\displaystyle D}$ ${\displaystyle E}$, ${\displaystyle F}$, отличен от нуля. Является частным случаем квадрики.

Поверхности второго порядка, получающиеся при различных значениях параметров уравнения

Типы поверхностей второго порядка

Цилиндрические поверхности

Поверхность ${\displaystyle S}$ называется цилиндрической поверхностью с образующей ${\displaystyle {\vec {l}}}$, если для любой точки ${\displaystyle M_{0}}$ этой поверхности прямая, проходящая через эту точку параллельно образующей ${\displaystyle {\vec {l}}}$, целиком принадлежит поверхности ${\displaystyle S}$.

Теорема (об уравнении цилиндрической поверхности).
Если в некоторой декартовой прямоугольной системе координат поверхность ${\displaystyle S}$ имеет уравнение ${\displaystyle f(x,y)=0}$, то ${\displaystyle S}$ — цилиндрическая поверхность с образующей, параллельной оси ${\displaystyle OZ}$.

Кривая, задаваемая уравнением ${\displaystyle f(x,y)=0}$ в плоскости ${\displaystyle z=0}$, называется направляющей цилиндрической поверхности.

Если направляющая цилиндрической поверхности задаётся кривой второго порядка, то такая поверхность называется цилиндрической поверхностью второго порядка.

Эллиптический цилиндр:	Параболический цилиндр:	Гиперболический цилиндр:
${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}$	${\displaystyle y^{2}=2px}$	${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}\!=1}$
Пара совпавших прямых:	Пара совпавших плоскостей:	Пара пересекающихся плоскостей:
${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=0}$	${\displaystyle y^{2}=0}$	${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}\!=0}$

Конические поверхности

Коническая поверхность.

Основная статья: Коническая поверхность

Поверхность ${\displaystyle S}$ называется конической поверхностью с вершиной в точке ${\displaystyle O}$, если для любой точки ${\displaystyle M_{0}}$ этой поверхности прямая, проходящая через ${\displaystyle M_{0}}$ и ${\displaystyle O}$, целиком принадлежит этой поверхности.

Функция ${\displaystyle F(x,y,z)}$ называется однородной порядка ${\displaystyle m}$, если ${\displaystyle \forall t\in \mathbb {R} \;\forall x,y,z}$ выполняется следующее: ${\displaystyle F(tx,ty,tz)=t^{m}F(x,y,z)}$

Теорема (об уравнении конической поверхности).
Если в некоторой декартовой прямоугольной системе координат поверхность ${\displaystyle S}$ задана уравнением ${\displaystyle F(x,y,z)=0}$, где ${\displaystyle F(x,y,z)}$ — однородная функция, то ${\displaystyle S}$ — коническая поверхность с вершиной в начале координат.

Если поверхность ${\displaystyle S}$ задана функцией ${\displaystyle F(x,y,z)}$, являющейся однородным алгебраическим многочленом второго порядка, то ${\displaystyle S}$ называется конической поверхностью второго порядка.

• Каноническое уравнение конуса второго порядка имеет вид:

${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=0}$

Поверхности вращения

Поверхность ${\displaystyle S}$ называется поверхностью вращения вокруг оси ${\displaystyle OZ}$, если для любой точки ${\displaystyle M_{0}(x_{0},y_{0},z_{0})}$ этой поверхности окружность, проходящая через эту точку в плоскости ${\displaystyle z=z_{0}}$ с центром в ${\displaystyle (0,0,z_{0})}$ и радиусом ${\displaystyle r={\sqrt {x_{0}^{2}+y_{0}^{2}}}}$, целиком принадлежит этой поверхности.

Теорема (об уравнении поверхности вращения).
Если в некоторой декартовой прямоугольной системе координат поверхность ${\displaystyle S}$ задана уравнением ${\displaystyle F(x^{2}+y^{2},z)=0}$, то ${\displaystyle S}$ — поверхность вращения вокруг оси ${\displaystyle OZ}$.

Эллипсоид:	Однополостной гиперболоид:	Двуполостной гиперболоид:	Эллиптический параболоид:	Гиперболический параболоид:
${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}+{\frac {z^{2}}{c^{2}}}=1}$	${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=1}$	${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=-1}$	${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=2z}$	${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=2z}$

В случае, если ${\displaystyle a=b\neq 0}$, перечисленные выше поверхности являются поверхностями вращения.

Эллиптический параболоид

Уравнение эллиптического параболоида имеет вид

${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=2z.}$

Если ${\displaystyle a=b}$, то эллиптический параболоид представляет собой поверхность вращения, образованную вращением параболы, параметр которой ${\displaystyle p=a^{2}=b^{2}}$, вокруг вертикальной оси, проходящей через вершину и фокус данной параболы.

Пересечение эллиптического параболоида с плоскостью ${\displaystyle z=z_{0}>0}$ является эллипсом.

Пересечение эллиптического параболоида с плоскостью ${\displaystyle x=x_{0}}$ или ${\displaystyle y=y_{0}}$ является параболой.

Гиперболический параболоид

Уравнение гиперболического параболоида имеет вид

${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=2z.}$

Пересечение гиперболического параболоида с плоскостью ${\displaystyle z=z_{0}}$ является гиперболой.

Пересечение гиперболического параболоида с плоскостью ${\displaystyle x=x_{0}}$ или ${\displaystyle y=y_{0}}$ является параболой.

Ввиду геометрической схожести гиперболический параболоид часто называют «седлом».

Центральные поверхности

Если центр поверхности второго порядка существует и единственен, то его координаты ${\displaystyle \left(x_{0},\;y_{0}\;z_{0}\right)}$ можно найти, решив систему уравнений:

${\displaystyle {\begin{cases}a_{11}x_{0}+a_{12}y_{0}+a_{13}z_{0}+a_{14}=0\\a_{21}x_{0}+a_{22}y_{0}+a_{23}z_{0}+a_{24}=0\\a_{31}x_{0}+a_{32}y_{0}+a_{33}z_{0}+a_{34}=0\end{cases}}}$

Матричный вид уравнения поверхности второго порядка

Уравнение поверхности второго порядка может быть переписано в матричном виде:

${\displaystyle {\begin{pmatrix}x&y&z&1\end{pmatrix}}{\begin{pmatrix}a_{11}&a_{12}&a_{13}&a_{14}\\a_{21}&a_{22}&a_{23}&a_{24}\\a_{31}&a_{32}&a_{33}&a_{34}\\a_{41}&a_{42}&a_{43}&a_{44}\end{pmatrix}}{\begin{pmatrix}x\\y\\z\\1\end{pmatrix}}=0}$

Также можно выделить квадратичную и линейную части друг от друга:

${\displaystyle {\begin{pmatrix}x&y&z\end{pmatrix}}{\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{pmatrix}}{\begin{pmatrix}x\\y\\z\end{pmatrix}}+2{\begin{pmatrix}a_{14}&a_{24}&a_{34}\end{pmatrix}}{\begin{pmatrix}x\\y\\z\end{pmatrix}}+a_{44}=0}$

Если обозначить ${\displaystyle A={\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{pmatrix}}\quad b={\begin{pmatrix}a_{14}&a_{24}&a_{34}\end{pmatrix}}\quad X={\begin{pmatrix}x&y&z\end{pmatrix}}^{T}}$ , то уравнение приобретает следующий вид:

${\displaystyle X^{T}AX+2bX+a_{44}=0}$

Инварианты

Значения следующих величин сохраняются при ортогональных преобразованиях базиса:

• Связанных с матрицей ${\displaystyle A}$:
  • ${\displaystyle I_{1}=\mathrm {tr} \,A}$
  • ${\displaystyle I_{2}={M_{A}}_{1,2}^{1,2}+{M_{A}}_{1,3}^{1,3}+{M_{A}}_{2,3}^{2,3}}$, где ${\displaystyle {M_{A}}_{i,j}^{i,j}}$ — минор второго порядка матрицы A, расположенный в строках и столбцах с индексами i и j.
  • ${\displaystyle I_{3}=\det A}$

• Связанных с блочной (расширенной) матрицей ${\displaystyle B={\begin{pmatrix}A&b\\b^{T}&a_{44}\end{pmatrix}}}$^[1]
  • ${\displaystyle K_{1}=\sum _{i=1}^{3}\sum _{j=i+1}^{4}{M_{B}}_{i,j}^{i,j}}$
  • ${\displaystyle K_{2}=\sum _{i=1}^{2}\sum _{j=i+1}^{3}\sum _{k=j+1}^{4}{M_{B}}_{i,j,k}^{i,j,k}}$
  • ${\displaystyle K_{4}=\det B}$

Такие инварианты также иногда называют полуинвариантами или семи-инвариантами.

При параллельном переносе системы координат величины ${\displaystyle I_{1},I_{2},I_{3},K_{4}}$ остаются неизменными. При этом:

• ${\displaystyle K_{2}}$ остается неизменной только если ${\displaystyle I_{2}=I_{3}=K_{4}=0}$
• ${\displaystyle K_{1}}$ остается неизменной только если ${\displaystyle I_{2}=I_{3}=K_{4}=K_{2}=0}$

Классификация поверхностей второго порядка относительно значений инвариантов

Для любой алгебраической поверхности второго порядка существует такая декартова система координат, в которой уравнение этой поверхности принимает один из следующих семнадцати канонических видов:

Поверхность	Уравнение	Инварианты
Эллипсоид	${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}+{\frac {z^{2}}{c^{2}}}=1}$	${\displaystyle I_{3}\neq 0}$	${\displaystyle I_{2}>0,\quad I_{1}I_{3}>0}$	${\displaystyle K_{4}<0}$
Мнимый эллипсоид	${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}+{\frac {z^{2}}{c^{2}}}=-1}$			${\displaystyle K_{4}>0}$
Точка	${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}+z^{2}=0}$			${\displaystyle K_{4}=0}$
Однополостный гиперболоид	${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=1}$		${\displaystyle I_{2}\leq 0}$ или ${\displaystyle I_{1}I_{3}\leq 0}$	${\displaystyle K_{4}>0}$
Двуполостный гиперболоид	${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=-1}$			${\displaystyle K_{4}<0}$
Конус	${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-2z^{2}=0}$			${\displaystyle K_{4}=0}$
Эллиптический параболоид	${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-2z=0}$	${\displaystyle I_{3}=0}$	${\displaystyle K_{4}\neq 0}$	${\displaystyle K_{4}<0}$
Гиперболический параболоид	${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}-2z=0}$			${\displaystyle K_{4}>0}$
Эллиптический цилиндр	${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}$		${\displaystyle K_{4}=0}$	${\displaystyle I_{2}>0}$	${\displaystyle I_{1}K_{2}<0}$
Мнимый эллиптический цилиндр	${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=-1}$				${\displaystyle I_{1}K_{2}>0}$
Прямая (пара мнимых пересекающихся плоскостей)	${\displaystyle {\frac {x^{2}}{a^{2}}}+y^{2}=0}$				${\displaystyle K_{2}=0}$
Гиперболический цилиндр	${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}$			${\displaystyle I_{2}<0}$	${\displaystyle K_{2}\neq 0}$
Пара пересекающихся плоскостей	${\displaystyle {\frac {x^{2}}{a^{2}}}-y^{2}=0}$				${\displaystyle K_{2}=0}$
Параболический цилиндр	${\displaystyle y^{2}=2px}$			${\displaystyle I_{2}=0}$	${\displaystyle K_{2}\neq 0}$
Пара параллельных плоскостей	${\displaystyle x^{2}-d^{2}=0}$				${\displaystyle K_{2}=0}$	${\displaystyle K_{1}<0}$
Пара мнимых параллельных плоскостей	${\displaystyle x^{2}+d^{2}=0}$					${\displaystyle K_{1}>0}$
Плоскость	${\displaystyle x^{2}=0}$					${\displaystyle K_{1}=0}$