Проекция Мольвейде

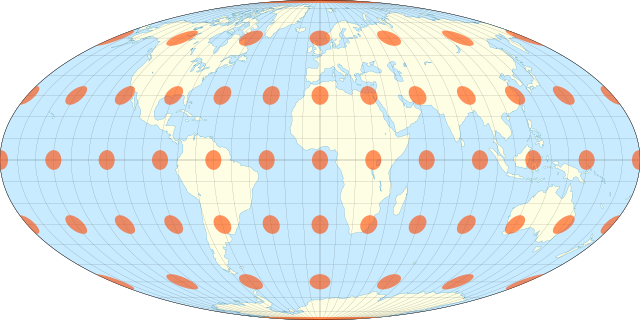
Проекция Мольвейде — равновеликая псевдоцилиндрическая картографическая проекция. Также известна как проекция Бабине, а также эллиптическая, гомолографической или гомалографической проекция. Обычно используется для представления карты мира или небесной сферы. Термин равновеликая обозначает, что проекция сохраняет соотношение площадей объектов, но искажает их форму.

Карта мира в проекции Мольвейде

Проекция Мольвейде с эллипсами искажений

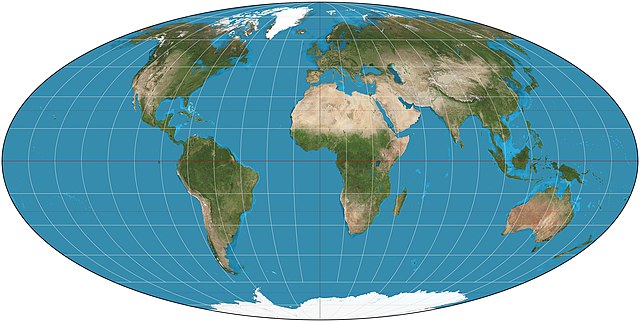
Проекция впервые была опубликована в 1805 году саксонским математиком и астрономом Карлом Мольвейде (1774—1825) в Лейпциге. В 1857 году Жак Бабинэ повторно изобрел эту проекцию и популяризовал ее под именем гомалографической. Во многие атласы XIX в. эта проекция вошла как гомолографическая.^[1]

Карта реликтового излучения в проекции Мольвейде, полученная по результатам 9 лет наблюдения спутника WMAP.^[2][3]

Карта содержания фреона на уровне моря в проекции Мольвейде, измеренная Global Ocean Data Analysis Project^[англ.].

Свойства

Проекция Мольвейде псевдоцилиндрическая, в которой экватор задан прямой горизонтальной линией, перпендикулярной центральному меридиану. Длина центрального меридиана равна половине длины проецированного экватора. Меридианы, отстоящие на ${\displaystyle 90^{\circ }}$ к западу и востоку от центрального, вместе образуют окружность, тогда как все прочие меридианы изображаются равномерно распределенными полуэллипсами. Вся карта представляет собой эллипс с отношением осей 2:1. Все параллели представляют собой прямые линии, перпендикулярные центральному меридиану. Расстояние между ними уменьшается по мере удаления от экватора. Отношении между площадями на карте такие же, как как между соответствующими площадями на земном шаре, но их форма искажается, в особенности при приближении к периметру эллипса, хотя и в меньшей степени по сравнению с синусоидальной проекцией.

На основе проекции Мольвейде были созданы другие картографические проекции, например Ван дер Гринтена, Гуда или Боггса^[4]

Математическое выражение

Проекция образуется путем трансформации широты ${\displaystyle \varphi }$ и долготы ${\displaystyle \lambda }$ в координаты x и y на карте с помощью следующих выражений:^[5]

${\displaystyle {\begin{aligned}x&=R{\frac {2{\sqrt {2}}}{\pi }}\left(\lambda -\lambda _{0}\right)\cos \theta ,\\[5px]y&=R{\sqrt {2}}\sin \theta ,\end{aligned}}}$

где ${\displaystyle \theta }$ — вспомогательный угол, определяемый из уравнения

${\displaystyle 2\theta +\sin 2\theta =\pi \sin \varphi ,\qquad (1)}$

${\displaystyle \lambda _{0}}$ — долгота центрального меридиана карты, а R — радиус проецируемой сферы. Площадь карты составляет ${\displaystyle 4\pi R^{2}}$, что соответствует площади поверхности проецируемой сферы. Координата x заключена в диапазоне [−2R√2, 2R√2], а координата y — в диапазоне [−R√2, R√2].

Уравнение (1) может быть решено численно методом Ньютона-Рафсона:^[5]

${\displaystyle {\begin{aligned}\theta _{0}&=\varphi ,\\\theta _{n+1}&=\theta _{n}-{\frac {2\theta _{n}+\sin 2\theta _{n}-\pi \sin \varphi }{2+2\cos 2\theta _{n}}}.\end{aligned}}}$^{[note 1]}

Если ${\displaystyle \varphi =\pm {\frac {\pi }{2}}}$, то и ${\displaystyle \theta =\pm {\frac {\pi }{2}}}$. Уравнение (1) решается аналитически, хотя в итерационной формуле получается неопределенность типа ${\displaystyle {\frac {0}{0}}}$.

Существует аналитическое выражение для обратного преобразования:^[5]

${\displaystyle {\begin{aligned}\varphi &=\arcsin {\frac {2\theta ^{\prime }+\sin 2\theta ^{\prime }}{\pi }},\\[5px]\lambda &=\lambda _{0}+{\frac {\pi x}{2R{\sqrt {2}}\cos \theta ^{\prime }}},\end{aligned}}}$

где ${\displaystyle \theta ^{\prime }}$ может быть определено из уравнения

${\displaystyle \theta ^{\prime }=\arcsin {\frac {y}{R{\sqrt {2}}}}.\,}$

Обратные преобразования позволяют найти широту и долготу, соответствующие координатам на карте x и y.

См. также

• Список картографических проекций
• Синусоидальная проекция
• Гиперэллиптическая проекция Тоблера

Примечания

1. Формула в тексте помогает читателю подтвердить, что формула верна. Для численного вычисления следует изменить знаменатель, начиная с формулы двойного угла.

   ${\displaystyle {\begin{aligned}\cos 2\theta _{n}&=2\cos ^{2}\theta _{n}-1,\\1+\cos 2\theta _{n}&=2\cos ^{2}\theta _{n},\\2+2\cos 2\theta _{n}&=4\cos ^{2}\theta _{n},\\\theta _{n+1}&=\theta _{n}-{\frac {2\theta _{n}+\sin 2\theta _{n}-\pi \sin \varphi }{4\cos ^{2}\theta _{n}}}.\end{aligned}}}$

   В численных вычислениях исходный знаменатель стремится к нулю для ${\displaystyle \theta }$ вблизи ${\displaystyle \pm {\frac {\pi }{2}}}$ (катастрофическое сокращение). Эта замена верна для всех углов и позволяет избежать проблемы вблизи ${\displaystyle \theta =\pm {\frac {\pi }{2}}}$, не делая ее особым случаем.